Теория систем автоматического управленияО записи линеаризованных уравнений звеньев
В теории автоматического управления в настоящее время принято записывать дифференциальные уравнения звеньев в двух стандартных формах.
Первая форма записи. Дифференциальные уравнения записываются так, чтобы выходная величина и ее производные находились в левой части уравнения, а входная величина и все остальные члены — в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Чтобы привести линеаризованное уравнение (3.5) к такому виду, введем обозначения:
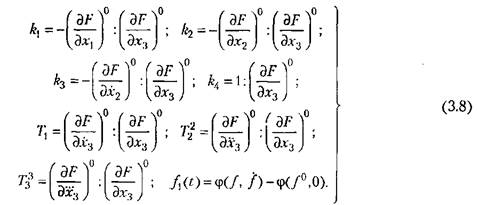
Тогда уравнение (3.5) примет вид
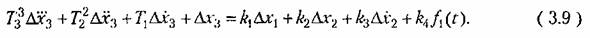
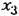 , а содержит только ее производные, т. е. если , а содержит только ее производные, т. е. если
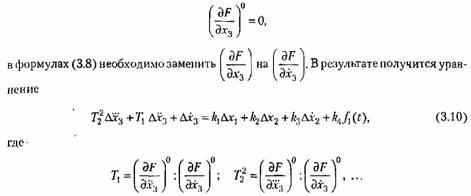
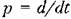 . Тогда уравнение (3.9) . Тогда уравнение (3.9)
примет вид
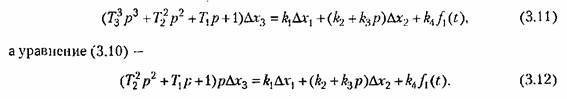
Эти записи надо рассматривать только как сокращенную форму более полных записей (3.9) и (3.10).
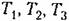 — постоянными времени данного звена. — постоянными времени данного звена.
В случае звеньев, у которых выходная и входная величины имеют одинаковую размерность, для коэффициентов передачи используются также следующие термины:
1) коэффициент усиления — для звена, представляющего собой усилитель или имеющего в своем составе усилитель;
2) передаточное число — для редукторов, делителей напряжения, масштабирующих устройств и т. д.
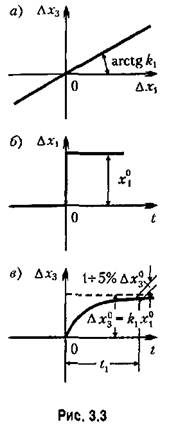
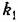 показывает отношение выходной величины звена к входной в установившемся режиме. показывает отношение выходной величины звена к входной в установившемся режиме.
Следовательно, коэффициент передачи определяет собой наклон (с учетом масштабов по осям) линейной статической характеристики звена (рис. 3.3, а). Заметим, что нелинейную характеристику звена часто называют характеристикой с неременной по входной величине коэффициентом передачи. Из (3.9) очевидно, что
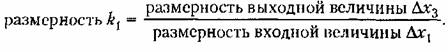
В размерность коэффициента передачи может входить также время t. Так, из уравнения (3.9) следует, что
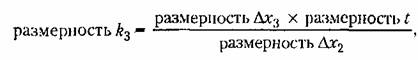
а из уравнения (3.10) следует, что для такого звена
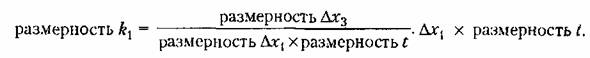
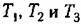 , как следует из уравнений (3.9) и (3.10), имеют размерность времени. , как следует из уравнений (3.9) и (3.10), имеют размерность времени.
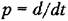 алгебраической величиной, решим уравнение (3.11) относительно выходной величины: алгебраической величиной, решим уравнение (3.11) относительно выходной величины:
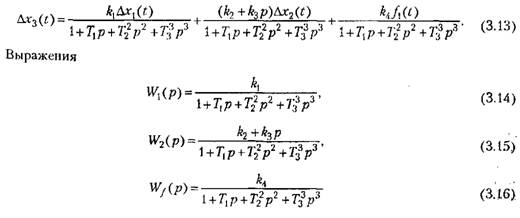
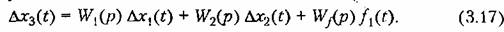 в виде в виде
Выражения (3.13) и (3.17) представляют собой символическую запись дифференциального уравнения (3.9).
Передаточные функции, формулы для которых устанавливаются выражениями (3.14)—(3.16), вводятся для сокращения записи дифференциальных уравнений и также представляют собой символическую закись дифференциальных уравнений.
Более строго передаточная функция определяется через изображения Лапласа (см. главу 7). Если ввести изображения по Лапласу входных и выходных величин звена:
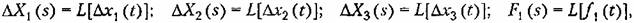
 — комплексная величина, то передаточную функцию (3,14) можно строго определить как отношение изображений выходной и входной величин звена: — комплексная величина, то передаточную функцию (3,14) можно строго определить как отношение изображений выходной и входной величин звена:
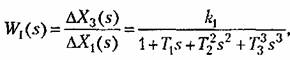
при нулевых начальных условиях и равных нулю остальных воздействиях на звено;
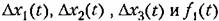 можно написать при пулевых начальных условиях уравнение для изображений в виде, совпадающем но форме с (3.17): можно написать при пулевых начальных условиях уравнение для изображений в виде, совпадающем но форме с (3.17):
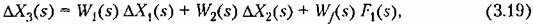
или в развернутом виде:
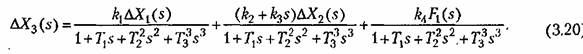
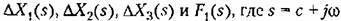 — комплексная величина, — комплексная величина,
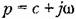 . В этом случае уравнение (3.19) будет иметь вид . В этом случае уравнение (3.19) будет иметь вид
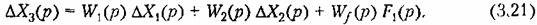
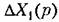
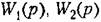 и т, д. Однако в передаточных функциях буква/? будет означать символ дифференцирования и т, д. Однако в передаточных функциях буква/? будет означать символ дифференцирования

в зависимости от того, рассматриваются ли функции времени или их изображения.
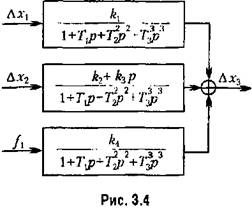
Понятие передаточной функции весьма удобно при анализе так называемых структурных схем. Так, например, звено, изображенное на рис. 3.1, после линеаризации, которая была проделана в предыдущем параграфе, можно представить в виде структурной схемы, показанной на рис. 3.4. Передаточные функции звеньев или отдельных участков схемы позволяют легко получить общее уравнение всей системы в виде (3.13) или (3.20), а в дальнейшем в случае необходимости перейти к исходному дифференциальному уравнению вида (3.9). Подобным же образом могут быть получены передаточные функции и структурные схемы и для других дифференциальных уравнений звеньев, например для рассмотренного выше уравнения (3.10).
|