Теория систем автоматического управленияНепрерывные линейные системы автоматического управления
Линеаризация
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Линеаризация уравнений
При составлении дифференциальных уравнений динамики любой автоматической системы последнюю разбивают на отдельные звенья и записывают уравнение каждого звена в отдельности. Уравнения всех звеньев образуют единую систему которую можно преобразовать к одному уравнению путем исключения промежуточных переменных,
Уравнение звена должно быть составлено так, чтобы оно выражало зависимость (в динамическом процессе) между теми величинами, которые в схеме исследуемой системы указаны на выходе и входе данного звена, т. е. между величинами, представляющими воздействие данного звена на последующее по схеме звено и воздействие предыдущего звена па данное. Динамическое уравнение отдельного звена составляется но правилам соответствующей технической науки (звено может представлять собой тепловой двигатель, электрическую машину механическую передачу, электрическую цепь и т. п.).
Звено может иметь иногда не одну входную величину, а несколько (например, при наличии дополнительных обратных связей). Кроме входной и выходной величин звена, которые выражают собой внутренние связи между звеньями данной системы, может учитываться также внешнее воздействие.
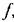 а динамическое Уравнение звена имеет произвольный нелинейный вид а динамическое Уравнение звена имеет произвольный нелинейный вид
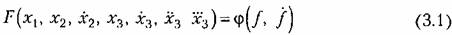
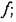 вообще же здесь могут быть любые другие варианты). вообще же здесь могут быть любые другие варианты).
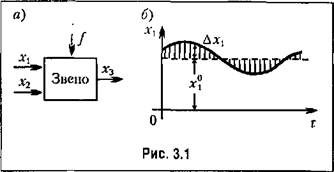
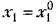 , ,
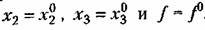 . Тогда уравнение установившегося состояния для данного звена согласно (3.1) будет . Тогда уравнение установившегося состояния для данного звена согласно (3.1) будет
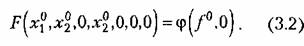
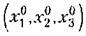 остаются все время достаточно малыми (рис. 3.1, б). остаются все время достаточно малыми (рис. 3.1, б).
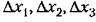 . Тогда в динамическом процессе . Тогда в динамическом процессе
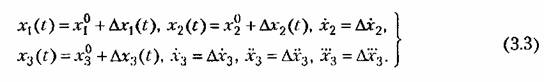
Условие достаточной малости динамических отклонений переменных от некоторых установившихся значений для системы автоматического управления обычно выполняется. Этого требует сама идея работы замкнутой автоматической системы.
Внешнее же воздействие не зависит от работы автоматической системы, изменение его может быть произвольным, и поэтому правая часть уравнения (3.1) обычно линеаризации не подлежит (в отдельных случаях и она может быть линеаризована).
Первый способ линеаризации. Разложим функцию Р, стоящую в левой части уравнения (3.1), в ряд по степеням указанных выше малых отклонений, рассматривая все производные тоже как самостоятельные переменные. Тогда, уравнение (3.1) примет вид
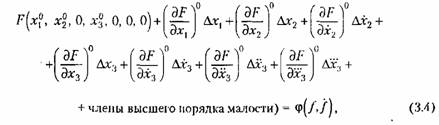
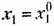
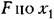 , после чего в нее вместо всех переменных подставляются , после чего в нее вместо всех переменных подставляются
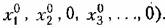
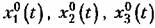
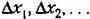 с коэффициентами в виде смешанных частных производных и частных производных второго и высших порядков от функции F по всем переменным. с коэффициентами в виде смешанных частных производных и частных производных второго и высших порядков от функции F по всем переменным.
Вычтя из уравнения (3.4) почленно уравнение установившегося состояния (3.2) и отбросив члены высшего порядка малости, получим искомое линеаризованное уравнение динамики данного звена в виде
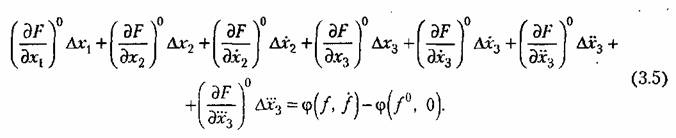
Это дифференциальное уравнение, так же как и (3.1), описывает тот же динамический процесс в том же звене автоматической системы. Отличие этого уравнения от прежнего состоит в следующем:
это уравнение является приближенным, ибо в процессе его вывода были отброшены малые высшего порядка;
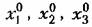 ; ;
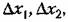
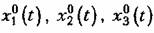 , например при программном управлении. , например при программном управлении.
Таким образом, цель получения линейного дифференциального уравнения взамен прежнего нелинейного достигнута. Уравнение (3.5) называется дифференциальным уравнением звена в отклонениях. Проделав то же самое для всех звеньев системы, получим в результате линеаризованные уравнения процесса управления в отклонениях (или, как называют еще, уравнения в вариациях),
В дальнейшем можно будет проводить линеаризацию нелинейных уравнений непосредственно по аналогии с формулой (3.5), не производя предварительных выкладок.
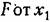 при постоянных значениях всех остальных переменных: при постоянных значениях всех остальных переменных:
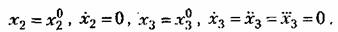
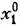 и проведем в точке С касательную. Тогда и проведем в точке С касательную. Тогда
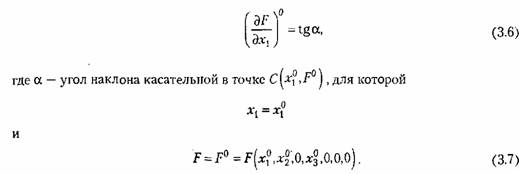
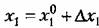 и сокращение члена (3.7), производившиеся раньше аналитически, здесь эквивалентны переносу начала координат в точку С (рис. 3.2, а), в результате чего получается график рис. 3.2, б. и сокращение члена (3.7), производившиеся раньше аналитически, здесь эквивалентны переносу начала координат в точку С (рис. 3.2, а), в результате чего получается график рис. 3.2, б.
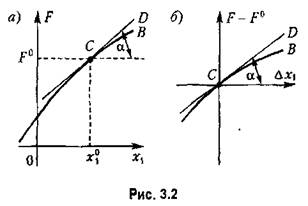
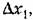 для которых допустима линеаризация, тем шире, чем ближе кривая СВ к прямой СО. Последним обстоятельством и определяются практически в каждой задаче те границы, внутри которых отклонения можно считать достаточно малыми. для которых допустима линеаризация, тем шире, чем ближе кривая СВ к прямой СО. Последним обстоятельством и определяются практически в каждой задаче те границы, внутри которых отклонения можно считать достаточно малыми.
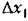 .Линеаризация может быть совершенно недопустимой при скачкообразных зависимостях (например, при релейных характеристиках). Такого рода зависимости называются существенно нелинейными. .Линеаризация может быть совершенно недопустимой при скачкообразных зависимостях (например, при релейных характеристиках). Такого рода зависимости называются существенно нелинейными.
Важно отметить следующее. Если по указанным причинам не может быть подвергнуто линеаризации уравнение только одного звена системы или даже только часть функции F для данного звена, то производят линеаризацию всех остальных нелинейных зависимостей, оставляя только одну или несколько существенно нелинейных.
Второй способ линеаризации. Из приведенной геометрической иллюстрации вытекает другой способ линеаризации уравнений системы автоматического регулирования, который весьма часто применяется на практике. Этот способ заключается в том, что с самого начала все криволинейные зависимости, используемые при составлении уравнений звеньев, заменяются прямолинейными (по касательной в соответствующей точке кривой). Тогда уравнения звеньев сразу будут получаться линейными.
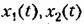 и т. д. будет опускаться в предположении, что эти переменные представляют собой малые отклонения от некоторого установившегося состояния и линеаризация уравнений уже проделана. и т. д. будет опускаться в предположении, что эти переменные представляют собой малые отклонения от некоторого установившегося состояния и линеаризация уравнений уже проделана.
|