Теория систем автоматического управленияНелинейные системы автоматического управления
СОСТАВЛЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Общие понятия
Нелинейной системой автоматического управления называется такая система, которая содержит хотя бы одно звено, описываемое нелинейным уравнением. Перечислим виды нелинейных звеньев:
звено релейного тина (рис. 1.12);
звено с кусочно-линейной характеристикой (рис. 1.10, д и др.);
звено с криволинейной характеристикой любого очертания;
звено, уравнение которого содержит произведение переменных или их производных и другие их комбинации;
нелинейный импульсный элемент;
логическоезвено;
звенья, описываемые кусочно-линейными дифференциальными уравнениями, в том числе неременной структуры.
Различают статические и динамические нелинейности. Первые описываются нелинейными алгебраическими уравнениями, а вторые представляются в виде нелинейных дифференциальных уравнений.
Общий метод составления уравнений для нелинейных систем состоит в следующем. Сначала по правилам §3.1 производится линеаризация уравнений всех звеньев системы, для которых это допустимо, кроме существенно нелинейных звеньев (чате всего одпого-двух). Затем составляются уравнения этих последних звеньев со всеми допустимыми упрощениями их характеристик.
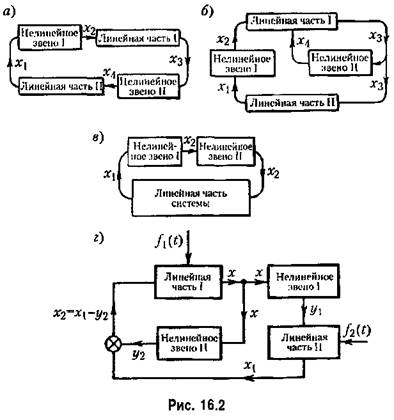
В результате получается система линейных уравнений, к которым добавляется одно-два (иногда более) нелинейных. В соответствии с этим обобщенную структурную схему любой нелинейной системы в случае одного нелинейного звена можно представить в виде рис. 16.1, а, где линейная часть может иметь структуру любой сложности (с обратными связями и т. п„ как, например, на рис. 16.1, били в). В случае двух нелинейных
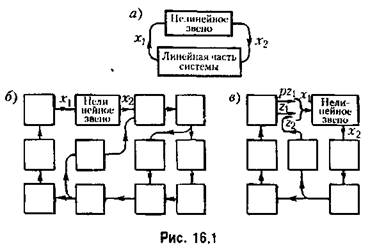
звеньев могут быть разные комбинации, в зависимости от того, в какие цепи системы они холят (см., например, рис. 16.2).
Часто при исследовании нелинейных систем удается выделить нелинейность так, чтобы она описывалась непосредственно зависимостью между выходной и входной величинами
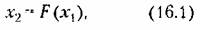
которая может иметь любую форму (релейного типа, кусочно-линейного или криволинейного). Но иногда, как будет показано в следующих параграфах, не удается этого сделать и приходится исследовать нелинейные дифференциальные зависимости вида

Встречаются и более сложные случаи, когда обе величины (входная и выходная) оказываются под знаком нелинейной функции раздельно:
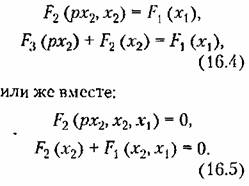
Разделим все нелинейные системы на два больших класса.
1 . К первому классу отнесем такие, в которых Уравнение нелинейного звена приводится к любому из видов (16.1)-(16.3), т. е. когда под знаком нелинейной функции стоит только входная величина (и ее производные) либо только выходная величина (и ее производные). При этом имеется в виду, что схема системы в целом может быть приведена к виду рис. 16.1 с одним нелинейным звеном. К этому классу сводится также случай с двумя нелинейными звеньями, указанный на рис. 16.2, я, так как там они могут быть объединены в одно нелинейное звено. Сюда же относится и случаи, покапанный на рис. 16.2, г, где имеются два нелинейных звена (если их уравнения содержат под знаком нелинейности только входную величину х, например, вида (16.1) или (16.2)).
2 . Второй к л а с с нелинейных систем включает системы с любым числом нелинейных звеньев, когда под знаки нелинейных функций входят различные переменные, связанные между собой линейной передаточной функцией. Так будет в случае системы с одним нелинейным звеном вида (16.4) или (16.5), а также в системе с двумя нелинейными звеньями (рис. 16.2, а или г), если в нервом из них под знак нелинейности входит входная величина, а во втором - выходная. Система же рис, 16.2, б относится ко второму классу, если под знаки нелипейпоетей входят в обоих звеньях либо только входные, либо только выходные величины нелинейных звеньев.
Ко второму класcу нелинейных систем относятся также системы с двумя и более нелипейноетями, в уравнениях которых под знаки нелинейных функций входят разные переменные, связанные между собой нелинейными дифференциальными уравнениями (т. е. связанные через линейные части и нелинейные звенья). К таким системам относятся, например, система на рис. 16,2, а, если в ее уравнения х под знаками нелинейных функций находятся входные (пли выходные) величины обоих нелинейных звеньев, и многие другие системы.
Системы с логическими устройствами относятся обычно к нелинейным системам второго класса.
Заметим, что во всех случаях, когда под знак нелинейной функции входит какая-либо линейная комбинация разных переменных, их следует обозначать одной буквой, а данную линейную комбинацию учесть при составлении общего уравнения линейной части системы. Это бывает, например, в тех случаях, когда на вход нелинейного звена подаются производные или включается обратная связь. Так. если для рис. 16.1,6

можно привести уравнение нелинейного звена к виду (16.1 )
Из всех уравнений линейных звеньев, а также добавочных линейных выражений типа (16.6), получаемых при выделении нелинейности, составляется общее уравнение линейной части системы

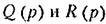 — операторные многочлены, или передаточная функция линейной — операторные многочлены, или передаточная функция линейной
части системы

Составление уравнений будет проиллюстрировано ниже на примерах.
Процессы в нелинейных системах автоматического управления имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах.
Благодаря этим существенным особенностям даже вопрос об устойчивости системы становится здесь более сложным. Кроме структуры системы и значений ее параметров для устойчивости того или иного установившегося процесса в отличие от линейных систем имеют значение также и начальные
условия. Возможен новый вид установившегося процесса - автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе возникают автоколебания, то установившееся состояние, соответствующее постоянному значению управляемой величины, становится невозможным.
Следовательно, в общем случае на плоскости параметров системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постоянным значением управляемой величины; 2) область автоколебаний; 3) область неустойчивости системы; 4) области, соответствующие другим, более сложным случаям.
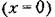 системы системы
устойчиво в малом, т. е. при начальных условиях, не выводящих отклонения в переходном процессе за определенную величину а, и неустойчиво в большом, т. е. при начальных условиях, выводящих отклонение в переходном процессе за пределы величины а. Здесь граничным процессом является неустойчивый периодический процесс собственного движения системы с амплитудой а (переходные процессы расходятся от него и обе стороны).
II р и м е р. Для иллюстрации особенностей нелинейной системы исследуем переходный процесс и автоколебания в релейной системе стабилизации температуры. Для этого составим сначала уравнения управляемого объекта и управляющего устройства.
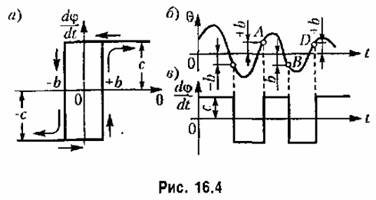
Пусть объект представляет собой некоторую камеру. Учитывая инерционность процесса нагрева и охлаждения запишем его уравнение в виде
 , а входной — 0 (рис, 16.4, а). , а входной — 0 (рис, 16.4, а).
Следовательно, уравнение управляющего устройства запишется следующим образом:

 ) в данной системе (участки AВ и ВD па рис. 16.4, б). ) в данной системе (участки AВ и ВD па рис. 16.4, б).
На участке ЛВ уравнение управляющего устройства согласно рис. 16.4, в будет
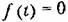 следующее уравнение системы на участке ЛВ: следующее уравнение системы на участке ЛВ:

а на участке BD

Условимся для простоты отсчитывать время Сот начала участка AВ (рис. 16.5, а). Тогда начальные условия будут
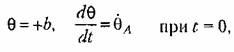
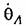 пока неизвестно. Используя начальные условия, находим произвольные постоянные для уравнения (16,15): пока неизвестно. Используя начальные условия, находим произвольные постоянные для уравнения (16,15):
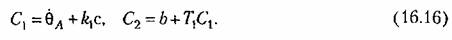
Аналогично для участка ВО согласно (16.13), отсчитывая время г тоже от начала этого участка (рис. 16.5, б), получим решение

Все остальные участки кривой переходного процесса будут определяться, очевидно,

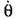 в конце предшествующих им участков. Поэтому, если в конце предшествующих им участков. Поэтому, если
будет задана величина 6 в начальной точке первого участка процесса, то все вышена-писанное решение для переходного процесса в системе станет определенным. Такой метод решения задачи называется методом припасоаывапия.
Выясним теперь, возможны ли в данной системе автоколебания, т. е, устойчивое периодическое решение. Для этого нужно, очевидно, чтобы в конце D одного периода
 , какие были в , какие были в
начале его А, Легко заметит!), что при этом оба полупериода (AB и BD) должны быть одинаковыми вследствие симметрии характеристики (рис. 16.4, а). Поэтому для определения автоколебаний достаточно рассмотреть только один участок АВ и потребовать, чтобы

Обозначив период искомых автоколебаний через 2Г. а длительность участка AB, через Т, из (16.14) найдем
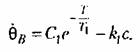
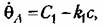 получаем выражение получаем выражение

 Из (16.15) (16.16) при этом находим Из (16.15) (16.16) при этом находим
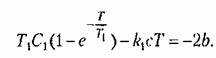
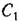 из (16.19), получим уравнение для определения полунериода авто колебаний: из (16.19), получим уравнение для определения полунериода авто колебаний:
Это трансцендентное уравнение для легко решается графически (рис. 16.6) пересечением двух кривых:

Если найдено вещественное положительное значение для У, то это свидетельствует о наличии периодического решения
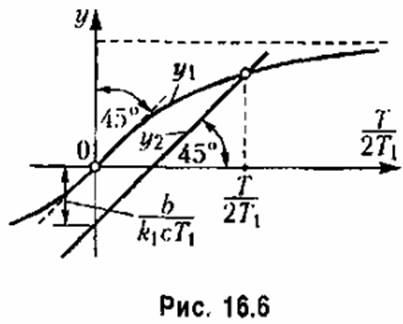
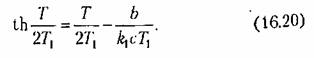
в дайной системе. Чтобы доказать, что это соответствует автоколебаниям, нужно исследовать их устойчивость, т. е. показать, что в переходном процессе система ведет себя, как изображено на рис. 16.3, я, по не так, как на рис. 16.3,6. Это будет показано ниже.
 па участке ЛВ па участке ЛВ
(рис. 16.5, а) путем исследования функции (16.15) па максимум обычным путем.
Фазовое пространство. Для наглядного представления о сложных нелинейных процессах управления часто прибегают к понятию фазового пространства, которое заключается в следующем. Дифференциальное уравнение замкнутой системы я-го порядка можно преобразовать к системе п дифференциальных уравнений первого порядка в виде
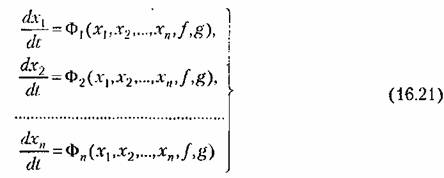
с начальными условиями

 — вспомогательные переменные; — вспомогательные переменные;
 — возмущающее и задающее воздействия. — возмущающее и задающее воздействия.
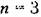 (система третьего порядка). (система третьего порядка).
 здесь могут иметь любой физический смысл. Но условно их можно представить как прямоугольные координаты некоторой точки М(рис. 16.7, а). здесь могут иметь любой физический смысл. Но условно их можно представить как прямоугольные координаты некоторой точки М(рис. 16.7, а).
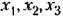 определенным образом изменяются. Это соответствует перемещению точки Мв пространстве но определенной траектории. Следовательно, траектория Движения точки Л/может служить наглядной геометрической иллюстрацией поведения системы в процессе управления. определенным образом изменяются. Это соответствует перемещению точки Мв пространстве но определенной траектории. Следовательно, траектория Движения точки Л/может служить наглядной геометрической иллюстрацией поведения системы в процессе управления.
 называется фазовым пространством. называется фазовым пространством.
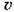 изображающей точки М (рис. 16.7, а) на оси координат. Следовательно, по значениям правых частей уравнений (16.21) в каждый момент времени можно судить о паправлении движения изображающей точки М, а вместе с тем и о поведении соответствующей реальной системы. изображающей точки М (рис. 16.7, а) на оси координат. Следовательно, по значениям правых частей уравнений (16.21) в каждый момент времени можно судить о паправлении движения изображающей точки М, а вместе с тем и о поведении соответствующей реальной системы.
482 Нелинейные системы автоматического управления

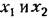 (система второго порядка), то изображающая точка будет двигаться не в пространстве, а на плоскости (фазовая плоскость). (система второго порядка), то изображающая точка будет двигаться не в пространстве, а на плоскости (фазовая плоскость).
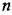 -мерным. -мерным.
Итак, фазовое пространство и фазовые траектории представляют собой лишь геометрический образ процессов, протекающих в системе. В этом геометрическом представлении участвуют координаты и исключено время. Фазовая траектория сама по себе дает лишь качественное представление о характере поведения системы. Чтобы определить количественно положение изображающей точки (а значит, и состояние системы) в любой момент времени, нужно найти решение заданных дифференциальных уравнений (16.21) во времени.
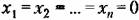 . Следовательно, изображением установившегося состояния системы является начало координат фазового пространства. . Следовательно, изображением установившегося состояния системы является начало координат фазового пространства.
Отсюда вытекает, что фазовые траектории устойчивой линейной системы будут асимптотически приближаться к началу координат при неограниченном увеличении времени. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.
Для нелинейной системы вследствие ряда особенностей процессов, отмечавшихся выше, фазовые траектории могут принимать самые разнообразные очертания. Если имеется асимптотическая устойчивость для определенного круга начальных условий, то все фазовые траектории, которые начинаются внутри определенной области Г), окружающей начало координат фазового пространства (рис. 16.7, б), будут асимптотически приближаться к началу координат. Если устойчивость неасимптотическая, то фазовые траектории, начинающиеся внутри области Т| могут иметь любые очертания, но не будут выходить за пределы некоторой определенной области е, окружающей начало координат (рис. 16.7, б).
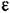 (рис. 16.7, б) можно найти такую область Г), что при начальных условиях, расположенных внутри этой области, возмущенное движение (переходный процесс) будет таким, что изображающая точка не выйдет из области е при любом сколь угодно большом значении времени. (рис. 16.7, б) можно найти такую область Г), что при начальных условиях, расположенных внутри этой области, возмущенное движение (переходный процесс) будет таким, что изображающая точка не выйдет из области е при любом сколь угодно большом значении времени.
 , что при начальных условиях решение дифференциальных уравнений возмущенного движения (переходного процесса) удовлетворяет неравенствам , что при начальных условиях решение дифференциальных уравнений возмущенного движения (переходного процесса) удовлетворяет неравенствам
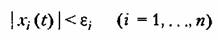
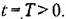
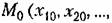
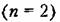 он обращается в прямоугольник. Аналогично и он обращается в прямоугольник. Аналогично и
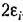
В формулировке Ляпунова содержится требование сколь угодной малости указанных областей. Однако практически это определение, так же как и теоремы Ляпунова, которые будут приведены ниже, применяется и тогда, когда эти области имеют определенные конечные размеры.
Фазовые траектории для обыкновенных линейных систем. Пусть переходный процесс в некоторой системе описывается уравнением второго порядка

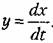 Тогда уравнение системы (16.23) преобразуется к виду Тогда уравнение системы (16.23) преобразуется к виду
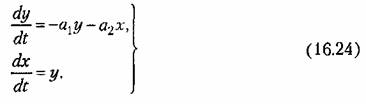
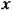


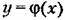 этого дифференциального уравнения с одной произвольной по- этого дифференциального уравнения с одной произвольной по-
стоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (х,у), каждая из которых соответствует одному определенному значению произвольной постоянной.
Вся совокупность интегральных кривых представит собой все возможные фазовые траектории, а значит, и все возможные виды переходного процесса в дайной системе при любых начальных условиях.
Рассмотрим отдельно различные случаи. Уравнению (16.23) соответствуют корни характеристического уравнения
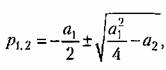
причем возможны шесть случаев:
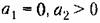 (колебательная граница устойчивости линейной системы); (колебательная граница устойчивости линейной системы);
 (устойчивая линейная система); (устойчивая линейная система);
 (неустойчивая линейная система); (неустойчивая линейная система);
 (устойчивая линейная система); (устойчивая линейная система);
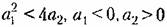 (неустойчивая линейная система); (неустойчивая линейная система);
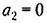 (апериодическая граница устойчивости линейной системы). (апериодическая граница устойчивости линейной системы).
Случай 1. В первом случае получаются, как известно, незатухающие колебания (рис. 16.8, а)

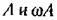 (рис. 16.8, б). Уравнение эллипса (рис. 16.8, б). Уравнение эллипса


причем Л -- произвольная постоянная

интегрирования.
Итак, периодическим колебаниям системы (рис. 16.8, а) соответствует движение изображающей точки по замкнутой кривой (рис. 16.8,6).
Случай 2. В этом случае (комплексные корни с отрицательными вещественными частями), как известно, имеют место затухающие; колебания (рис. 16 9 а)
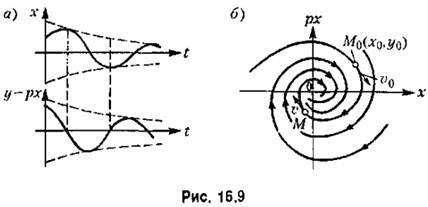
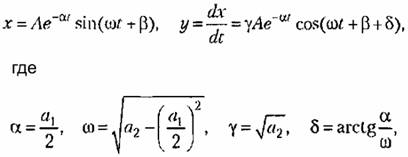
а произвольные постоянные A и (B определяются из начальных условий:
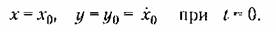
 не возвращаются за период колебания к прежним, а становятся не возвращаются за период колебания к прежним, а становятся
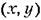 кривую (рис. 16.9, б), которая за один кривую (рис. 16.9, б), которая за один
оборот не возвращается в прежнюю точку М0, а подходит ближе к началу координат.
Итак, затухающим колебаниям системы (рис 16.9, а) отвечают фазовые траектории в виде спиралей, по которым изображающая точка приближается к началу координат (рис. 16.9,6).
С л уча и 3. Этот случай (комплексные корни с положительными вещественными частями) соответствует расходящимся колебаниям (рис. 16.10, а). Рассуждая аналогично предыдущему, получим всю совокупность возможных фазовых траекторий тоже в виде спиралей, но только изображающая точка будет двигаться но ним не к началу координат, а от него (рис. 16.10,6).

С л у ч а и 4. Этот случай (вещественные отрицательные корпи) соответствует апериодическому процессу
 это это
 а во втором варианте знаки х и у меняются по одному разу. Границы областей 1 и 2 представляют собой прямые а во втором варианте знаки х и у меняются по одному разу. Границы областей 1 и 2 представляют собой прямые
 (обращение одного из корней в нуль). (обращение одного из корней в нуль).
В отличие от прежнего здесь все фазовые траектории вливаются непосредственно в начало координат О фазовой плоскости. Однако изображающая точка Мне попадает в начало координат в конечное время, а приближается асимптотически.
Итак, затухающим апериодическим процессам в системе отвечают фазовые траектории, вливающиеся в начало координат.
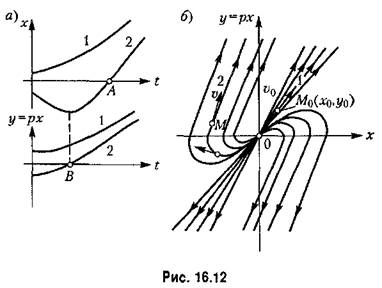
 Аналогично предыдущему получаем кривые процесса и фазовые траектории, изображенные на рис. 16.12. Аналогично предыдущему получаем кривые процесса и фазовые траектории, изображенные на рис. 16.12.
 имеют разные знаки, имеют разные знаки,
 то введем обозначение то введем обозначение
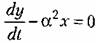 и согласно (16.25) — уравнению фазовых траекторий и согласно (16.25) — уравнению фазовых траекторий

Интегрирование последних аналогично случаю 1 дает
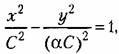 т. е. семейство гипербол, изображенное на рис т. е. семейство гипербол, изображенное на рис
16.13,6.
Направления движения изображающей точки М по фазовым траекториям, показанные на рис 16.13, б, легко определяются в

 (16.28). (16.28).
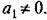
Итак, расходящимся апериодическим процессам в системе отвечают фазовые траектории тина рис. 16.12, били типа рис. 16.13,6, причем изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.
Особые точки. В точках, которые соответствуют установившемуся состоянию, получаем согласно (16.25) неопределенное выражение
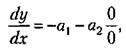
т. е. неопределенное направление касательных к интегральным кривым (фазовым траекториям). Такие точки называются особыми точками, причем для них существует следующая классификация:
а) особые точки типа точки О на рис. 16.8, б называются центрами,
б) особые точки типа рис. 16.9, б называются устойчивыми фокусами,
в) особые точки типа рис. 16.10, б называются неустойчивыми фокусами,
г) особые точки типа рис. 16.11, б называются устойчивыми узлами,
д) особые точки тина рис. 16.12, б называются неустойчивыми узлами,
е) особые точки типа рис. 16.13, б называются седлами (седло всегда неустойчиво).
|