Теория систем автоматического управленияСинтез непрерывных корректирующих средств
В импульсных системах (глава 14) Для коррекции используются непрерывные корректирующие средства. Наиболее просто производится расчет корректирующих средств последовательного типа. В этом случае дискретная передаточная функция разомкнутой системы должна равняться желаемой передаточной функции

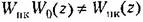
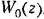 . Поэтому расчет последовательных корректирующих средств в дискретных системах не является столь простой задачей, как в непрерывных системах. . Поэтому расчет последовательных корректирующих средств в дискретных системах не является столь простой задачей, как в непрерывных системах.
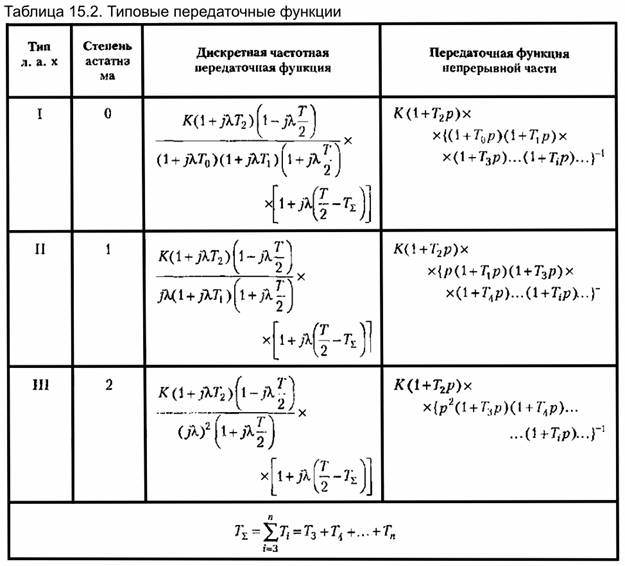
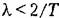 практически сливаются с л. а. х. непрерывной части. Поэтому можно воспользоваться известными приемами расчета последовательных корректирующих средств, если в качестве желаемых л. а. х. использовать характеристики, соответствующие передаточным функциям непрерывной части. практически сливаются с л. а. х. непрерывной части. Поэтому можно воспользоваться известными приемами расчета последовательных корректирующих средств, если в качестве желаемых л. а. х. использовать характеристики, соответствующие передаточным функциям непрерывной части.
Требуемый вид последовательного корректирующего звена определяется в этом случае по виду л. а. х., полученной вычитанием ординат л. а. х. нескорректированной системы из ординат желаемой (типовой) л. а. х.
Рассмотрим иллюстративный пример [9].
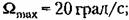 максимальное максимальное
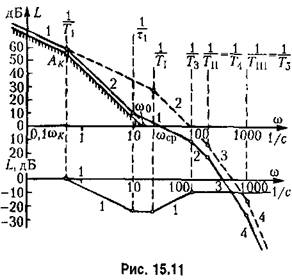
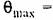 = 4 угл. мин.; допустимый показатель колебательности М = 1,5; период дискретности Т = 0,02 с; передаточная функция непрерывной части имеет вид = 4 угл. мин.; допустимый показатель колебательности М = 1,5; период дискретности Т = 0,02 с; передаточная функция непрерывной части имеет вид
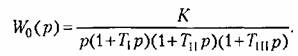
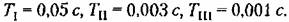
Определим вид и параметры последовательного корректирующего звена, которое должно быть включено в непрерывную часть системы, а также необходимое значение коэффициента незадачи разомкнутой системы К.
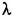 — с реальной частотой со. Поэтому формирование желаемой л. а. х. левее частоты среза произведем обычными приемами. — с реальной частотой со. Поэтому формирование желаемой л. а. х. левее частоты среза произведем обычными приемами.
Построим запретную зону для л. а. х. из условий точности (рис. 15.11). Контрольная частота
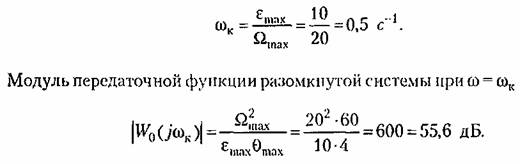
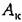 и запретная зона, сформированная из прямых с наклоном -20 и -40 дБ/дек (наклоны 1 и 2). и запретная зона, сформированная из прямых с наклоном -20 и -40 дБ/дек (наклоны 1 и 2).
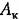 на 3 дБ. Она состоит из отрезков прямых с наклонами 1-2-1. В низкочастотной области частотная передаточная функция разомкнутой системы имеет вид на 3 дБ. Она состоит из отрезков прямых с наклонами 1-2-1. В низкочастотной области частотная передаточная функция разомкнутой системы имеет вид
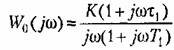
Параметры желаемой л. а. х. и передаточной функции разомкнутой системы в низкочастотной области определим в следующем порядке. Базовая частота л. а. х.
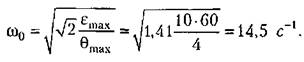
Постоянная времени корректирующего звена, формирующая первый взлом л. а. х.,
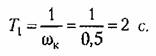
Для получения заданного показателя колебательности должно выдерживаться условие (формула 12.73)
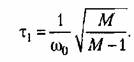
Отсюда получаем значение второй постоянной времени корректирующего звена:
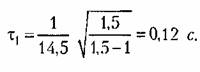
Далее определяем необходимое значение коэффициента передачи разомкнутой системы:
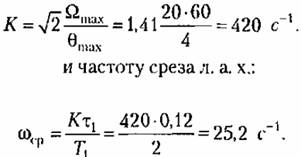
Для обеспечения заданного показателя колебательности в высокочастотной области должно удовлетворяться неравенство (15.49):
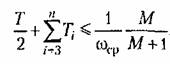
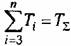 — сумма постоянных времени меньших, чем Г/2. — сумма постоянных времени меньших, чем Г/2.
Отсюда получаем допустимое значение для суммы постоянных времени:
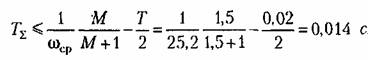
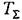 не превышала допустимого значения. не превышала допустимого значения.
Наиболее простые корректирующие звенья получаются в тех случаях, когда сопрягающие частоты л. а. х. нескорректированной системы и желаемой л. а. х. совпадают между собой. В рассматриваемом примере
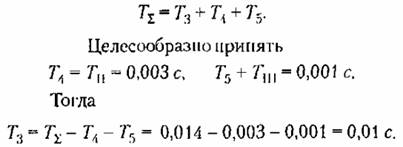
Вычитая из ординат желаемой л. а. х. ординаты характеристики нескорректированной системы, получим искомую л. а. х. последовательного корректирующего звена. Она соответствует интегро-дифференцирующему звену с передаточной функцией

Из приведенного примера видно, что при синтезе непрерывных последовательных корректирующих устройств метод логарифмических частотных характеристик не теряет своей простоты и наглядности. Более детально цифровые системы рассмотрены в работах [8,39,48].
|