Теория систем автоматического управленияУстойчивость и качество управления
Для систем с переменными параметрами понятие устойчивости имеет некоторую специфику. Если система работает ограниченный интервал времени, то понятие асимптотической устойчивости (см. § 6.1) практически теряет свой смысл. Однако Для квазистационарных систем при сравнительно медленном изменении коэффициентов уравнения (13.1) представляется возможным сформулировать понятие устойчивости следующим образом.
Будем считать систему с переменными параметрами устойчивой на заданном интервале времени 7", если ее нормальная функция веса (13.4) или (13.5) затухает во времени для всех фиксированных значений т>, лежащих внутри этого интервала. Это Условие можно записать следующим образом:
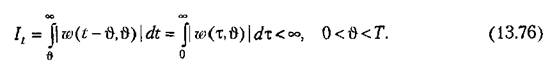
Если для системы получена нормальная функция веса, то вид ее и определяет устойчивость системы.
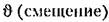 или 6 (реверс-смещение). Условие затухания вдоль этих аргументов можно записать следующим образом: или 6 (реверс-смещение). Условие затухания вдоль этих аргументов можно записать следующим образом:

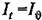 , определяемые формулами (13.76) и (13.77). , определяемые формулами (13.76) и (13.77).
Можно показать [86], что для систем, описываемых дифференциальным уравнением вида

выполнение условия (13.77) практически обеспечивает выполнение условия (13.76). В этих системах исследование устойчивости может быть проведено на базе параметрической передаточной функции.
Исследование затухания сопряженной функции веса может производиться как по ее виду, если она известна для рассматриваемой системы, так и па основании отсутствия полюсов параметрической передаточной функции замкнутой системы в правой полуплоскости и на мнимой оси. /Для этой цели могут привлекаться известные критерии устойчивости, например, критерий Найквиста и др.
 и передаточной функцией по ошибке и передаточной функцией по ошибке
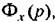 сохраняют свою силу и для параметрических передаточных функций. сохраняют свою силу и для параметрических передаточных функций.
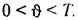



В соответствии с формулой (13,11) ошибку системы можно представить в виде
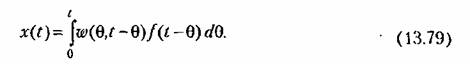
Разлагая задающее воздействие в ряд Тейлора около точки t и подставляя его в (1379), получаем

 — время затухания функции веса. Тогда верхний предел интегрирования в (13.80) можно положить равным бесконечности. В результате (13.80) можно представить в виде — время затухания функции веса. Тогда верхний предел интегрирования в (13.80) можно положить равным бесконечности. В результате (13.80) можно представить в виде

В отличие от коэффициентов ошибок системы с постоянными параметрами здесь они получаются зависящими от времени.
 Из (13.57) следует Из (13.57) следует

 получаем формулу для определения к-го коэффициента; получаем формулу для определения к-го коэффициента;

 на знаменатель так, чтобы получить ряд но возрастающим степеням р. на знаменатель так, чтобы получить ряд но возрастающим степеням р.
Коэффициенты ошибок могут также определяться для возмущающего воздействия но соответствующей функции веса или по параметрической передаточной функции относительно возмущающего воздействия.
|