Отыскание параметрической передаточной функции

Подставим эти значения в (13.1):

На основании (13.57) величины, находящиеся в квадратных скобках, можно представить в следующем виде:

В результате вместо (13.59) можно записать

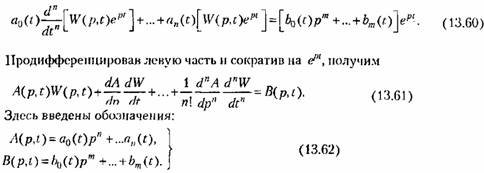
Таким образом, параметрическая передаточная функция может быть получена в результате решения дифференциального уравнения с переменными коэффициентами (13.61).

Заметим, что в системах с постоянными параметрами передаточная функция не зависит от времени и уравнение (13.61) приобретает вид

Передаточная функция в случае постоянства параметров будет

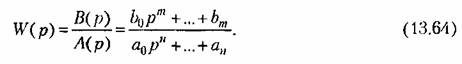
В случае переменных параметров уравнение (13.61) может быть решено методом последовательных приближений (86]. Для этого представим его в виде

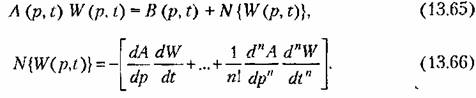
Будем искать решение в виде ряда

Первое приближение можно получить, положив N = 0 в (13.65):

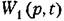подставим полученное из (13.68) пер-

вое приближение в правую часть (13.65), Тогда получим для первой поправки

Формула для к -й поправки будет иметь вид

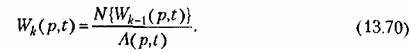
Таким образом, последующий член ряда (13.67) получается посредством дифференцирования предыдущего члена в соответствии с (13.66) и подстановки его в (1370).

Ряд (13,67) сходится тем быстрее, чем медленнее изменяются коэффициенты исходного дифференциального уравнения (13.1).

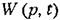может быть получена параметрическая частот-

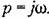
Использование параметрических передаточных функций. В соответствии с формулой (13.56) изображение Лапласа выходной величины системы с переменными параметрами можно найти как произведение изображения воздействия па параметрическую передаточную функцию:

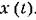
Для этой цели могут использоваться существующие таблицы изображений Лапласа функций времени. Так, например, пусть изображение выходной величины равно

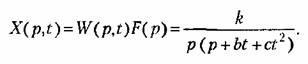
Полагая в этом выражении время фиксированным параметром, по таблице (см., например, табл. 7.2) находим

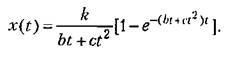
Если изображение представляет собой сложную дробио-рациональпую функцию, то можно использовать теорему разложения (см. § 7.4). При отсутствии нулевых корней знаменателя изображения

В формулах (13.73) и (13.75) корни знаменателя предполагаются некратными.