Теория систем автоматического управленияНелинейные алгоритмы управления
 управляющего устройства управляющего устройства
значительно расширяет возможности целесообразного изменения качества процессов управления. Это ясно из общих принципиальных соображений, так как область нелинейных уравнений значительно богаче и разнообразнее, чем линейных.
Несмотря на то, что общей теории нелинейных алгоритмов нет, исследования и опыт применения отдельных частных видов этих алгоритмов говорят об их большой практической эффективности. Отсюда следует актуальность их теоретического изучения.
Введем следующую классификацию нелинейных алгоритмов:
функциональные нелинейные алгоритмы;
логические нелинейные алгоритмы;
оптимизирующие нелинейные алгоритмы;
параметрические нелинейные алгоритмы.
Важным отличием нелинейных алгоритмов от линейных является то, что они придают системе принципиально новые свойства. Если при линейном алгоритме всегда вырабатывается сигнал, пропорциональный входной переменной или ее производной и т. д., то при нелинейном алгоритме может существенно изменяться сам характер действия системы управления на объект в зависимости от величины входного воздействия. Другими словами, если для линейных систем изменение размера отклонения — это изменение только масштаба, по не формы процессов, то в нелинейной системе при этом может существенно изменяться и форма процессов, вплоть до принципиальных качественных изменений картины процессов. Эти особые свойства нелинейных алгоритмов можно выгодно использовать в технике автоматического управления.
Рассмотрим отдельно каждый из указанных четырех классов нелинейных алгоритмов.
Функциональные нелинейные алгоритмы управления. Функциональными будем называть такие нелинейные алгоритмы, при которых управляющее воздействие на объект выражается в виде нелинейной функции от отклонения его величины, представляющей собой входную информацию для системы.
Данный класс может содержать в себе как статические, так и динамические нелинейности. Примеры статических пелинейностей:
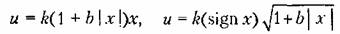
В отличие от линейного пропорционального, здесь в первом случае будет более энергичное действие управляющего устройства при больших отклонеииях-х и больший запас устойчивости установившегося режима. Во втором случае будет менее энергичное, но более плавное его действие вначале и повышенная точность в установившемся режиме, хотя и с меньшим запасом устойчивости. Однако такого рода рекомендации, как увидим в дальнейшем, справедливы для большинства систем, по все же не для всех. Поэтому они требуют специального обследования для каждого объекта.
Нелинейный алгоритм за счет дополнительных нелинейных обратных связей может включать в себя также нелинейности от выходной величины и:
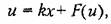
что расширяет возможности целесообразного изменения качества процесса управления.
Примеры динамических пелинейностей в алгоритме управления:
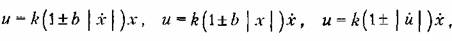
где вместо двойного знака подразумевается какой-либо один из них.
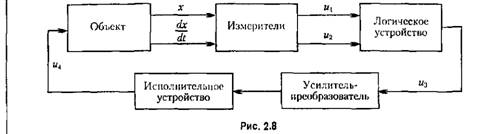
Подобные динамические члены различно влияют на демпфирующие свойства системы в переходных процессах в зависимости от размеров и скорости отклонения. Они же могут существенно улучшать динамическую точность (т. е. уменьшать динамические ошибки) системы в различных режимах вынужденного движения, воспроизведения различных форм задаваемых входных сигналов, а также при случайных воздействиях.
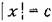 в системе может происходить переключение с одного линейного корректирующего устройства на другое. в системе может происходить переключение с одного линейного корректирующего устройства на другое.
Логические нелинейные алгоритмы управления. Нелинейные законы управления могут иметь иные формы, которые реализуются с помощью не функциональных, а более или менее сложных логических устройств. Будем называть их логическими нелинейными алгоритмами,
Например, в системе на рис. 2.8 логический нелинейный алгоритм может быть применен для экономии управляющих воздействий па объект (а также экономии расхода энергии па нужды управления).
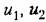 (рис. (рис.
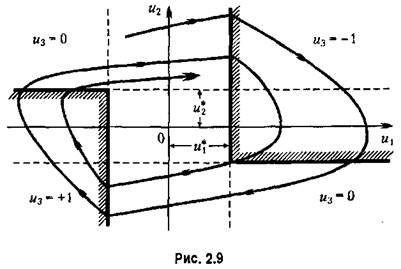
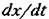 управляемой величины (рис. 2.8). управляемой величины (рис. 2.8).
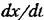 совпадает со знаком отклонениях, то величина отклонения х по модулю возрастает. В этом случае требуется энергичное действие управляющего устройства для его ликвидации. совпадает со знаком отклонениях, то величина отклонения х по модулю возрастает. В этом случае требуется энергичное действие управляющего устройства для его ликвидации.
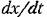 , Эти рассуждения позволяет считать целесообразным, например, применение следующего логического закона управления. , Эти рассуждения позволяет считать целесообразным, например, применение следующего логического закона управления.
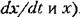 . Более подробно эта система будет рассмотрена в разделе IV, . Более подробно эта система будет рассмотрена в разделе IV,
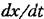 . Если правильно сформировать логику этих переключений, то можно существенно повысить качество работы системы. . Если правильно сформировать логику этих переключений, то можно существенно повысить качество работы системы.
Вместо комбинирования указанных линейных членов могут вводиться также и функциональные нелинейные члены; включение и выключение сигналов, соответствующих этим членам, производится при помощи логического устройства. Тогда получится комбинация функциональных и логических нелинейных алгоритмов.
Оптимизирующие нелинейные алгоритмы управления. Оптимальной называется автоматическая система, наилучшая в некотором смысле с учетом ограничений, накладываемых на величину управляющего воздействия, координаты, скорости и т. п. Это может быть, например, система, имеющая максимальное быстродействие, или минимальный расход энергии на управление, или максимальный коэффициент полезного действия,
Как правило, при этом приходят к нелинейным алгоритмам управления, хотя, вообще говоря можно оптимизировать и коэффициенты линейного алгоритма, задав его форму. Часто оптимальный нелинейный алгоритм состоит в переключении управляющего воздействия (при определенных состояниях системы) с одного максимально возможного значения на другие. Моменты переключения в целом определяются сложными комбинациями значений нескольких переменных и их производных.
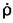 , т. е. тех величин, в которых выражена параметрическая программа. , т. е. тех величин, в которых выражена параметрическая программа.

Нелинейные алгоритмы управления обладают богатыми возможностями во всех случаях, когда требуемый эффект, может быть достигнут изменением свойств системы с изменением величин ошибок.
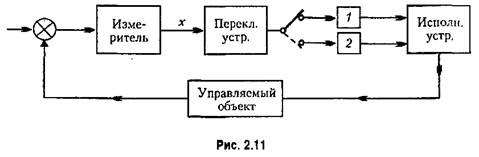
Большие дополнительные возможности улучшения процессов управления дает нелинейное управление работой объекта путем изменения структуры управляющего устройства в зависимости от размеров и знаков входных величин, поступающих от измерительного устройства.
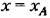 (рис. 2.11). (рис. 2.11).
Если в такой системе все звенья линейные, то за счет указанного переключения, происходящего автоматически в процессе управления, система становится нелинейной. Это можно сравнить с тем, как получается нелинейная статическая характеристика из отрезков прямых линий. Но здесь имеет место нелинейная динамическая характеристика, составляемая из последовательности разных линейных дифференциальных уравнений, соответствующих первому и второму алгоритмам управления.
В общем случае срабатывание переключающего устройства в системе с переменной структурой может происходить от нескольких входных величин. При этом кроме основной нелинейности, возникающей за счет переключения структуры, дополнительно могут иметься какие-либо нелинейные свойства в отдельных других звеньях управляющего устройства или объекта.
|