Теория систем автоматического управленияУстойчивость систем с распределенными параметрами
Системой автоматического управления с распределенными параметрами называется такая система, среди уравнений которой кроме обыкновенных дифференциальных уравнений имеются уравнения в частных производных. Физически это соответствует учету волновых явлений или гидравлического удара в трубопроводах, учету волновых процессов в длинных электрических линиях при передаче по ним воздействий от одного звена системы автоматического управления к другому или же при управлении процессами в самих трубопроводах или длинных линиях.
Этот вопрос приобретает практическое значение чаще всего в некоторых системах управления, включающих в себя водяные, масляные или газовые трубопроводы (либо в объекте, либо в управляющем устройстве), реже — в некоторых системах телерегулирования (телеуправления) и т. н.
Известно, например, что водяной трубопровод гидротурбины описывается без учета потерь уравнениями
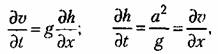
 — скорость движения воды; h — напор в произвольной точке, определяемой координатой х вдоль трубопровода; а — скорость звука в воде. — скорость движения воды; h — напор в произвольной точке, определяемой координатой х вдоль трубопровода; а — скорость звука в воде.

Уравнения длинной электрической линии без потерь имеют вид:
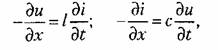
где и — напряжение; i — ток в произвольной точке, определяемой координатой х вдоль линии l и с — индуктивность и емкость единицы длины линии.
После решения указанных уравнений в частных производных с учетом граничных условий, определяемых смежными звеньями данной системы автоматического управления, для системы в целом получаются уравнения того же типа, как и для систем с запаздыванием (§ 6.7).
Рассмотрим вывод уравнений системы стабилизации давления газа в трубопроводе, схема которой изображена па рис. 6.27. В данном случае сам объект (трубопровод) является звеном с распределенными параметрами. Для простоты будем считать его прямолинейным, а всех потребителей — сосредоточенными па конце трубопровода.
 на объект выражается в изменении но произволу потребителей некоторого эквивалентного выходного сечения на конце трубопровода. на объект выражается в изменении но произволу потребителей некоторого эквивалентного выходного сечения на конце трубопровода.
Уравнение управляемого объекта. Движение газа в трубопроводе подчиняется уравнению

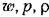 — соответственно скорость, давление и плотность газа — соответственно скорость, давление и плотность газа
 означают, что данные величины относятся к установившемуся состоянию системы. означают, что данные величины относятся к установившемуся состоянию системы.
Продифференцировав (6.51), получаем

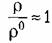 . В результате из уравнений (6.49), (6.50) и (6.52) получаем . В результате из уравнений (6.49), (6.50) и (6.52) получаем
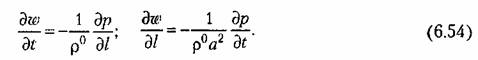
Ведем обозначения для относительного отклонения (р управляемой величины от ее установившегося значения и для относительной координаты А вдоль трубопровода:
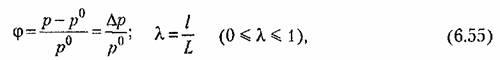
а также для относительного отклонения у скорости движения газа в трубопроводе:

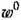 — скорость газа в трубопроводе при установившемся процессе; к — показатель степени р адиабатическом уравнении состояния газа (6.51). — скорость газа в трубопроводе при установившемся процессе; к — показатель степени р адиабатическом уравнении состояния газа (6.51).
Переходя в уравнениях (6.54) к этим относительным безразмерным переменным и бесконечно малым приращениям, получаем искомые уравнения управляемого объекта (трубопровода) в виде
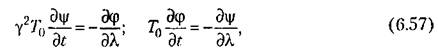
где введены два постоянных параметра управляемого объекта:

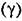 — отношение — отношение

установившейся скорости газа к скорости звука в нем.
Заметим, что уравнения (6.57) эквивалентны так называемому волновому уравнению
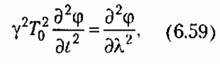
 а второе — но I и сравнить результаты дифференцирования, а второе — но I и сравнить результаты дифференцирования,
Для системы уравнений в частных производных (6.57) надо написать граничные
условия. Для этого запишем уравнение поступления газа через клапан в начале трубопровода и уравнение потребления газа в конце его.
Используем выражение для скорости газа через его расход, а именно:

где С — расход газа по весу в секунду; F — площадь сечения трубопровода; # - ускорение силы тяжести.
 перемещения клапанах, т. е. перемещения клапанах, т. е.
Эта функция (рис. 6.28) определяется либо аналитическим расчетом, либо из опытных данных.
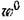 будет будет
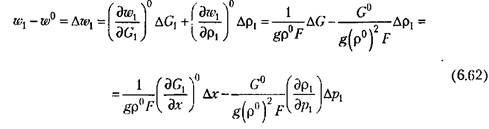
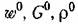 пишутся без индекса 1, так как они одинаковы пишутся без индекса 1, так как они одинаковы
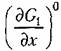 есть тангенс угла наклона касательной в точке С (рис. 6.28), соответствующей установившемуся процессу в трубопроводе. На основании (6.51) и (6.53) есть тангенс угла наклона касательной в точке С (рис. 6.28), соответствующей установившемуся процессу в трубопроводе. На основании (6.51) и (6.53)
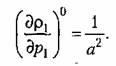
Введем безразмерную величину относительного отклонения управляющего клапана:

Подставляя все это в (6.62), с учетом (6.56) и (6.55) получаем уравнение поступления газа через управляющий клапан в начале трубопровода:

которое является первым граничным условием для уравнений объекта.
Расход газа в конце трубопровода у потребителей можно записать согласно (6.60) в виде

С другой стороны, известно, что при выходе газа из трубопровода (в случае критического истечения, которым мы для простоты и ограничимся) будет

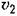 — удельный объем газа там же, — удельный объем газа там же,
Уравнение для отклонения величины расхода в процессе управления от его установившегося значения в линеаризованном виде на основании (6.67), (6.51), (6,65) и (6,55) будет
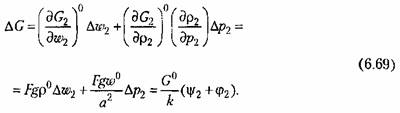


и вводя безразмерную величину изменения выходного сечения, т. е. внешнего возмущающего воздействия
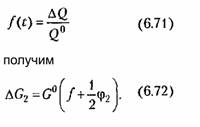
Сравнение выражений (6.69) и (6.72) даёт искомое уравнение потребление газа в конце трубопровода:

 у потребителей. При исследовании же переходного процесса в системе, когда после некоторого возмущения потребление установилось у потребителей. При исследовании же переходного процесса в системе, когда после некоторого возмущения потребление установилось
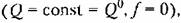 уравнение (6.73) будет иметь вид уравнение (6.73) будет иметь вид

Уравнение управляющего устройства. Уравнение чувствительного элемента

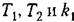 — постоянные времени и коэффициент передачи, а — постоянные времени и коэффициент передачи, а

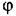 в уравнении (6.75) означает, что чувствительный элемент измеряет давление газа в начале трубопровода. в уравнении (6.75) означает, что чувствительный элемент измеряет давление газа в начале трубопровода.
Уравнение управляющего элемента со струйной трубкой

Уравнение пневматического двигателя будет

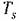 — время двигателя. — время двигателя.
Уравнение жесткой обратной связи согласно рис. 6.27 будет

|