Теория систем автоматического управленияИнтегрирующие звенья
1. Идеальное интегрирующее звено. Звено описывается дифференциальным уравнением
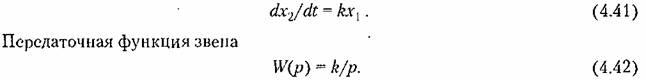
Такое звено является идеализацией реальных интегрирующих звеньев, часть которых будет рассмотрена ниже. Примеры интегрирующих звеньев приведены на рис. 4.18. Часто в качестве такого звена используется операционный усилитель в режиме интегрирования (рис. 4.18, а). Интегрирующим звеном является также обычный гидравлический демпфер (рис. 4.18, б). Входной величиной здесь является сила F, действующая на поршень, а выходной — перемещение поршня х2. Так как скорость движения поршня пропорциональна приложенной силе (без учета инерционных сил):
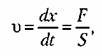
где 5 — коэффициент скоростного сопротивления; его перемещение будет пропорциональным интегралу от приложенной силы:
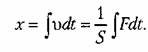
Часто в качестве интегрирующего звена используется интегрирующий привод (рис, 4.18, г). Это особенно удобно делать при необходимости длительного иитегрирования

(часы, дни и даже месяцы), например в автоматических путепрокладчиках и навигационных системах.
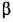 (в зоне линейности). (в зоне линейности).
Из уравнений гироскопа, приведенных в предыдущем параграфе, можно получить:
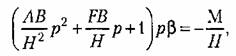
откуда передаточная функция для угла прецессии
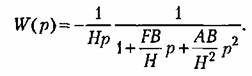
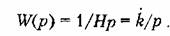
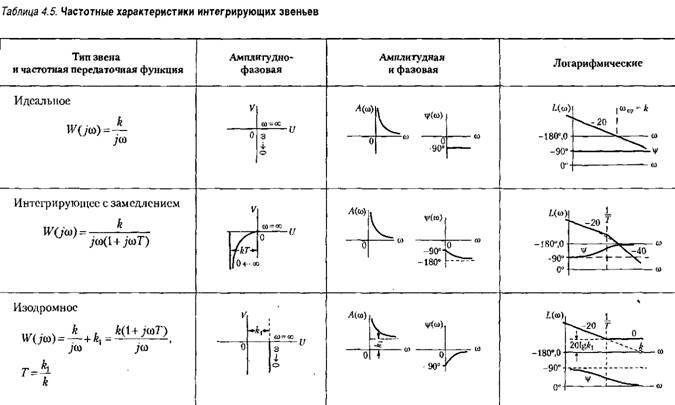
Временные характеристики звена приведены в табл. 4.4, а частотные — в табл. 4.5.
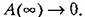
Амплитудно-фазовая характеристика сливается с отрицательной частью мнимой оси.
Построение л, а. х. делается но выражению

 , параллельную вещественной оси. , параллельную вещественной оси.

2. Интегрирующее звено с замедлением. Звено описывается дифференциальным уравнением
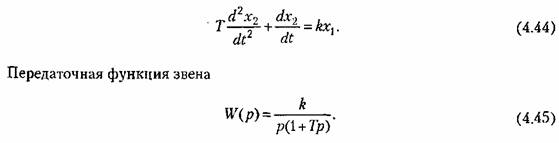
Примером такого звена является двигатель (рис. 4.10, а), если в качестве выходной величины рассматривать не угловую скорость, а угол поворота, являющийся интегралом от угловой скорости. К такому же типу звена сводятся демпфер (рис. 4.18, 6) серводвигатель (рис. 4.18, в), интегрирующий привод (рис. 4,18, г), если более точно рассматривать их уравнения движения, и др.
Интегрирующее звено с замедлением можно представить как совокупность двух включенных последовательно звеньев — идеального интегрирующего и апериодического первого порядка.
Для нахождения временных характера удобно передаточную функцию представить в виде алгебраической суммы
что позволяет представить решение дифференциального уравнения (4.44) в виде суммы решений для идеального интегрирующего звена и апериодического звена нервого порядка.
Временные характеристики приведены в табл.
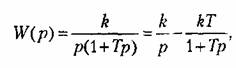
4.4, а частотные — в табл. 4.5.
Л.а.х. строится по выражению
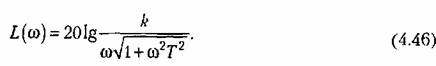
 и -40 дБ/дек (при со > 1/7). 3. Изодромное звено. Звено описывается уравнением и -40 дБ/дек (при со > 1/7). 3. Изодромное звено. Звено описывается уравнением
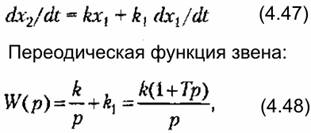
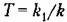 — постоянная времени изодромного звена. — постоянная времени изодромного звена.
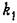 . .
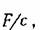
где с — жесткость пружины, и перемещения поршня
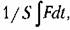
где 5 — коэффициент скоростного сопротивления демпфера.
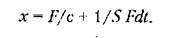 точки точки
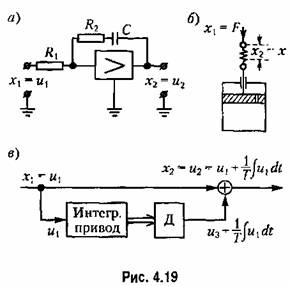
При использовании операционного усилителя (рис. 4.19, а) изодромное звено может быть получено посредством применения КС-цепи в обратной связи.
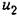
Таким образом, для схемы, изображенной на рис. 4.19, в,
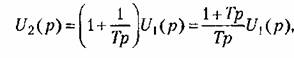
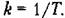
Временные характеристики звена представлены в табл. 4.4, а частотные — в табл. 4.5.
Л. а. х. строится по выражению
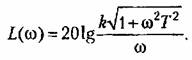
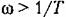
Из рассмотрения л. а. х. и л. ф. х. видно, что в области малых частот (меньших, чем сопрягающая частота) звено ведет себя как идеальное интегрирующее и тем точнее, чем меньше частота.
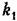
Свойство звена вводить интегрирующее действие в области малых частот используется для улучшения качественных показателей систем автоматического регулирования (см. главу 9).
|