Теория систем автоматического управленияПростейшие случайные процессы в нелинейных системах

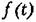 — внешнее воздействие, представляющее собой случайный процесс, причем — внешнее воздействие, представляющее собой случайный процесс, причем

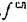 — —
центрированная случайная составляющая.
Пусть параметры системы таковы, что автоколебания отсутствуют и система устойчива относительно равновесного состояния. Применив статистическую линеаризацию (22.3) и подставив полученное выражение в заданное уравнение (22.15), разобьем последнее на два уравнения:
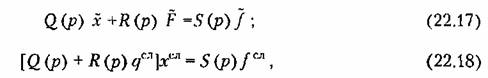
соответственно для регулярных (математических ожиданий) и случайных (центрированных) составляющих. При этом
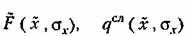
определяются для каждой заданной нелинейности, как указано в § 22.1. Рассмотрим в общем виде две различные задачи.
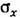 являются постоянными (имеет место некоторый установившийся режим) и уравнение (22.17) принимает алгебраический вид: являются постоянными (имеет место некоторый установившийся режим) и уравнение (22.17) принимает алгебраический вид:
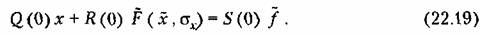
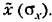 (22.20) (22.20)
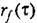 Линейная теория дает Линейная теория дает

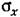 . Учитывая формулы (31.91) и (11.92), уравнение (22.21) можно записать в виде . Учитывая формулы (31.91) и (11.92), уравнение (22.21) можно записать в виде

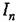 приведены в приложении 1). приведены в приложении 1).
 , т. е. полностью определится искомое приближенное решение1 уравнения (22.15): , т. е. полностью определится искомое приближенное решение1 уравнения (22.15):

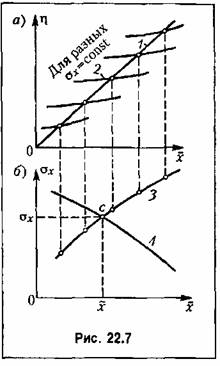
Это решение справедливо для случая установившегося режима при стационарном случайном процессе.
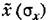 далеко не всегда можно выразить из уравнения (22.19) далеко не всегда можно выразить из уравнения (22.19)
 . Поэтому в большинстве случаев придется решать совместно два уравнения, (22.19) и (22.23), либо численно, путем последовательных приближений, либо графически. . Поэтому в большинстве случаев придется решать совместно два уравнения, (22.19) и (22.23), либо численно, путем последовательных приближений, либо графически.
Можно применять, например, следующий графический прием. Представим уравнение (22.19) в виде двух уравнений:
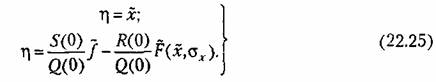
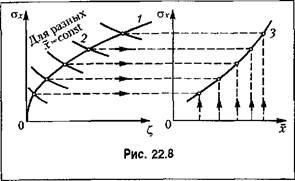
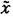 из кривой 3. Очевидно, что координаты точки из кривой 3. Очевидно, что координаты точки
пересечения С кривых 3 и 4 представляют собой искомый результат совместного решения уравнений (22.19) и (22.23).
Вторая з а л а ч а. Перейдем теперь к решению другой задачи, когда исследуется неустановившийся процесс.
 . Для этого по аналогии с графическим решением (21.25) разобьем уравнение (22.23) на два уравнения: . Для этого по аналогии с графическим решением (21.25) разобьем уравнение (22.23) на два уравнения:


 в вычисленное для заданной нелинейности согласно § 22.1 выражение в вычисленное для заданной нелинейности согласно § 22.1 выражение

 и получим функцию от заданной переменной и получим функцию от заданной переменной

 представляют собой смещения центра случайных составляющих. представляют собой смещения центра случайных составляющих.
Когда функция смещения (22.28) найдена, ее можно подставить в уравнение (22.17):
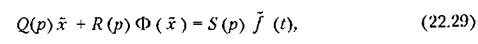

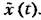
В большинстве задач функция смещения (22.28) будет иметь вид плавной кривой (рис. 22.9), которую в некоторых пределах можно подвергнуть обычной линеаризации

В случае, если система такова, что линейная часть с передаточной функцией

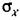 значительно упрощается, а значительно упрощается, а
именно из (22.21) следует

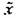
В этом случае вместо дифференцирования функции смещения (22.28) можно определить кп непосредственно из (22.27):
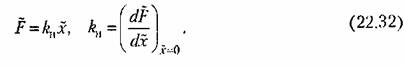


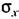 , найденную из формулы (22.31). , найденную из формулы (22.31).
 (см. приложение 2). (см. приложение 2).
В результате подстановки (22.30) или (22.32) уравнение для определения регулярной составляющей (22.29) станет линейным:
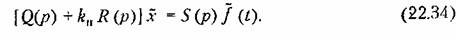
Оно решается при помощи обычного характеристического уравнения

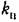 или даже становится неустойчивым. или даже становится неустойчивым.
Возможны случаи, когда это специфическое для нелинейных систем явление будет наступать раньше, чем система, рассчитанная как линейная, перестанет фильтровать полезный сигнал. С этой точки зрения учет фактически имеющихся в системе автоматического управления нелинейностей при наличии высокочастотных (по сравнению с полезным сигналом) помех является чрезвычайно важным для практики. Это столь же важно, как и учет влияния вибрационных синусоидальных помех, рассмотренный в § 21.2. Результаты решения обеих задач аналогичны.
Очевидно, что описанное специфическое для нелинейных систем влияние помех в некоторых случаях может и улучшать динамические качества системы.
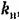 , учитывающему несправедливость принципа суперпозиции для нелинейных систем. , учитывающему несправедливость принципа суперпозиции для нелинейных систем.
 вытекающее из выражений (22.33) и (22.31) или (22.21). вытекающее из выражений (22.33) и (22.31) или (22.21).
|