Пример исследования влияния случайных помех

Пример исследования влияния случайных помех на динамику нелинейной системы

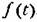, являющаяся высокочастотной по сравнению с медленно меняющимся полезным сигналом в данной системе. Проходя через нелинейное звено, помеха изменяет его коэффициент усиления по отношению к полезному сигналу (вторая задача § 22.2), Требуется оценить влияние этого явления на динамические качества данной системы автоматического управления по полезному сигналу.

Уравнение замкнутой системы (рис. 22.10) в целом будет

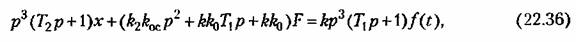
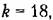
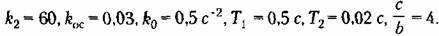
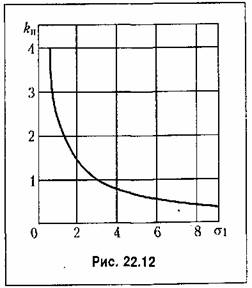
Помеха имеет нормальный закон распределения и задана спектральной плотностью (рис. 22.13)

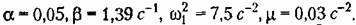
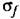
Произведя статистическую линеаризацию (22.3), разобьем уравнение системы (22.36) на два, соответственно для регулярной и случайной составляющих:

Поскольку передаточная функция линейной части системы

при заданных выше ее параметрах практически не пропускает частот, при которых спектральная плотность помехи (рис. 22.11) имеет существенное значение, то согласно (22.31) дисперсия помехи на входе нелинейного звена будет

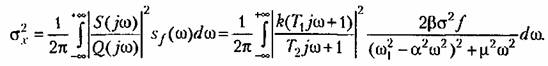
Чтобы привести этот интеграл к стандартному виду (§ 11.6), преобразуем сначала знаменатель спектральной плотности, а именно:

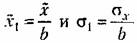. В начальной части все кривые этого графика близки к прямым. Поэтому можно провести их обычную линеаризацию в виде

~- крутизна в начале координат (рис. 22.6, б), которая зависит от величины а,. Для данной задачи получим

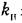является коэффициентом усиления полезного сигнала в нелинейном звене в присутствии помех, причем приведенная таблица дает зависимость этого коэффициента от уровня помехи, т. е. от среднеквадратичного ее значения

  , на входе нелинейного звена.

Как видим, увеличение уровня помехи ведет к существенному снижению коэффициента усиления полезного сигнала в нелинейном звене, что показано графически на рис. 22.12. Это составляет принципиальную особенность нелинейной системы, которая обусловливает зависимость всех ее статических и динамических качеств по полезному сигналу, в том числе и устойчивости, от уровня помех.

Найдем, например, зависимость устойчивости системы от уровня помех. Для этого согласно (22.38) и (22.41) запишем характеристическое уравнение системы:

Условие устойчивости системы по критерию Гурвица принимает вид

. Это согласно

рис. 22.12 соответствует значению

Эту величину удобно принять для выражения среднеквадратичного значения внешней помехи оув относительных

единицах, учитывая, что согласно

по формуле (22.40) при заданных выше параметрах системы, из (22.44) находим

Это означает, что только при уровне помех, не превышающем указанного значения, данная система остается устойчивой. Далее она теряет устойчивость по полезному сигналу.

, а по ней согласно (22.44) и среднеквадратичное значение внешней помехи, при которой теряется устойчивость системы:

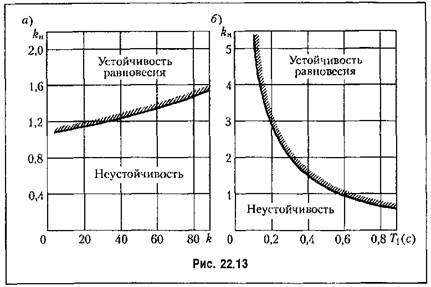
Это позволяет перестроить найденные на рис. 22.13 границы устойчивости в новые координаты соответственно

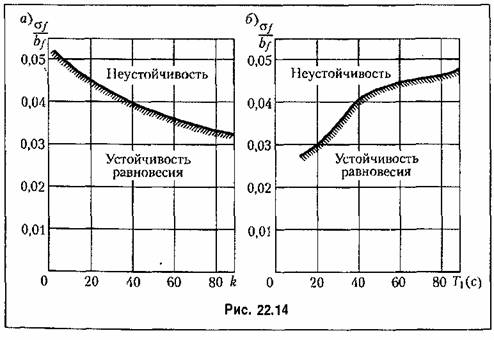
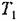является, согласно рис. 22.10, коэффициентом интенсивности введения производной, улучшающим стабилизацию системы.

По линейному уравнению, вытекающему из (22.38) и (22.41),

используя линейную теорию автоматического управления можно исследовать также и все другие динамические качества данной нелинейной системы по полезному сигналу в присутствии помех, учитывая, однако, при этом все время, что величина коэффициента кн зависит от уровня помех оу, от общей структуры и от некоторых параметров системы.