Теория систем автоматического управленияУстойчивость периодических решений
Выше уже указывалось, что не всякое периодическое решение уравнений собственного движения нелинейной системы будет соответствовать автоколебаниям, а только устойчивое. В конкретных задачах часто из физических соображений бывает сразу видно, возникают автоколебания или нет. Поэтому иногда нет нужды в математическом исследовании устойчивости найденного периодического решения. Однако в ряде случаев все же приходится этот вопрос исследовать.
Задача исследования устойчивости периодического решения сводится, вообще говоря, к анализу линейного уравнения с периодическими переменными коэффициентами. А. М. Ляпуновым [58] разработаны соответствующие методы. Но их использование во многих случаях представляет пока еще большие трудности. Поэтому здесь строгое исследование устойчивости периодических решений излагаться не будет.
Опишем три приближенных способа исследования устойчивости периодического решения: 1) осреднение коэффициентов; 2) использование кривой Михайлова; 3) аналитический критерий.
 Для линейной части системы на основании уравнения (18.31) получим Для линейной части системы на основании уравнения (18.31) получим

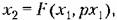 примет при этом для малых отклонений вид примет при этом для малых отклонений вид
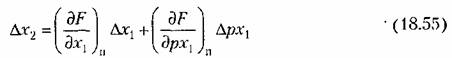
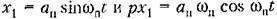 . Эти частные производные и являются периодическими переменными коэффициентами. В задачах теории управления они могут меняться как плавно, так и скачками (см. примеры в § 18.3). Осредпим полученные периодические коэффициенты, после чего вместо (18.55) будем иметь линейное уравнение с постоянными коэффициентами . Эти частные производные и являются периодическими переменными коэффициентами. В задачах теории управления они могут меняться как плавно, так и скачками (см. примеры в § 18.3). Осредпим полученные периодические коэффициенты, после чего вместо (18.55) будем иметь линейное уравнение с постоянными коэффициентами
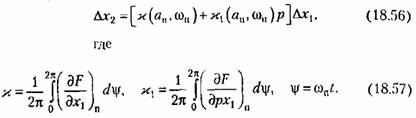
Характеристическое уравнение системы, определяющее устойчивость периодического решения, согласно (18.54) и (18.56) будет
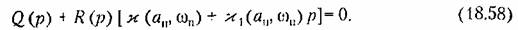
Если оно удовлетворяет линейному критерию устойчивости, то исследуемое периодическое решение устойчиво.
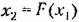 (с ш-стерезисной петлей или без нее), осредненное характеристическое уравнение для исследования периодического решения будет (с ш-стерезисной петлей или без нее), осредненное характеристическое уравнение для исследования периодического решения будет
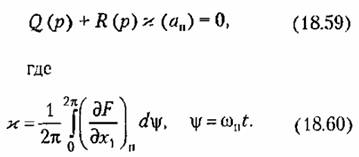
 она пройдет через начало координат (рис. 18.9). она пройдет через начало координат (рис. 18.9).
 охватывающая начато координат, соответствует затухающим колебаниям переходного процесса, а кривая 2 -расходящимся колебаниям. охватывающая начато координат, соответствует затухающим колебаниям переходного процесса, а кривая 2 -расходящимся колебаниям.
 расходятся. Следовательно, переходный процесс с обеих сторон схо дится к исследуемому периодическому процессу с амплитудой расходятся. Следовательно, переходный процесс с обеих сторон схо дится к исследуемому периодическому процессу с амплитудой
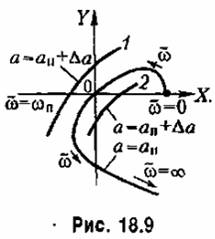
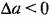 - кривая 1, - кривая 1,
то переходный процесс в обе стороны расходится, т. е. исследуемое периодическое решение неустойчиво (система устойчива в малом и неустойчива в большом, как па рис. 16.3, 6).
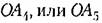 неустойчив. неустойчив.
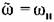 из начала координат с увеличением а определяется, очевидно, следующими проекциями на координатные оси X и У: из начала координат с увеличением а определяется, очевидно, следующими проекциями на координатные оси X и У:

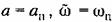 .Как видно из рис. .Как видно из рис.
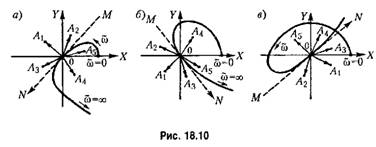
18.10, а, для устойчивости исследуемого периодического решения вектор, определяемый проекциями (18.61), должен лежать с определенной стороны от касательной МN к кривой Михайлова, направление которой в свою очередь определяется проекциями

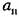
На рис. 18.10, б и в показаны те же векторы, что и на рис. 18.10, а, но для других видов кривых Михайлова. Видно, что во всех случаях для устойчивости исследуемого периодического решения требуется, чтобы вектор с проекциями (18.61) лежал справа от касательной МЫ, если смотреть вдоль кривой Михайлова в сторону возрастания
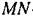 определяется вектором с проекциями (18.62). Это геометрическое условие устойчивости периодического решения можно записать в следующем аналитическом виде: определяется вектором с проекциями (18.62). Это геометрическое условие устойчивости периодического решения можно записать в следующем аналитическом виде:
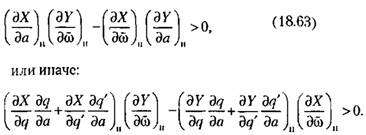
 (если она входит в коэффициенты, стоящие в квадратных скобках этого выражения). (если она входит в коэффициенты, стоящие в квадратных скобках этого выражения).
Выполнение условия (18.63) устойчивости периодического решения во всякой конкретной задаче можно проверить аналитически, без построения кривых. Этого достаточно для систем третьего и четвертого порядков, если все коэффициенты гармонически линеаризованного характеристического уравнения положительны. Для систем же пятого и более высокого порядков требуется дополнительно проверить общий ход кривой Михайлова, чтобы убедиться, что имеет место случай, например, рис. 18.11, а, по не рис. 18.11, б. Заметим, что вместо построения кривой Михайлова можно и тут воспользоваться аналитическим дополнительным условием, потребовав выполнения критерия Гурвица для многочлена

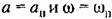 , при этом если О (р) имеет пятую или шестую степень, , при этом если О (р) имеет пятую или шестую степень,
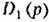
|