Теория систем автоматического управленияУстойчивость равновесного состояния системы.
Приведенные в начале данного параграфа гармонически линеаризованные уравнения нелинейной системы годятся только для колебательных процессов, определяемых периодическими решениями, и для колебательных переходных процессов в непосредственной близости от указанных периодических решений. Поэтому, строго говоря, с помощью этих приближенных уравнений можно анализировать только сами периодические
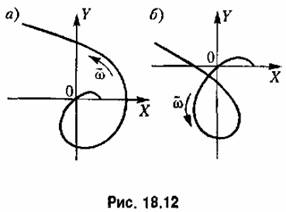
решения и их устойчивость или неустойчивость
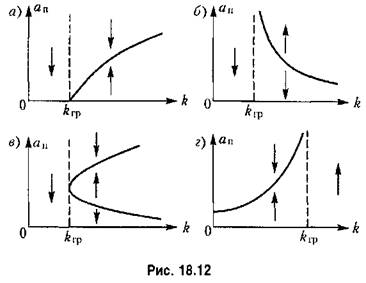
при малых отклонениях от исследуемого колебательного режима, что выше и делалось.
Практически же из анализа полученных приближенных уравнений нелинейной системы часто можно делать значительно более широкие выводы. В частности, можно оценивать устойчивость системы в тех областях ее параметров, в которых периодические решения отсутствуют вовсе.
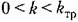 нет периодического решения) данная система будет устойчива, что также обозначено на рис. 18.12, а вертикальной стрелкой. нет периодического решения) данная система будет устойчива, что также обозначено на рис. 18.12, а вертикальной стрелкой.
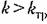 будет областью неустойчивости данной будет областью неустойчивости данной
нелинейной системы.
Наконец, если периодических решений для исследуемой нелинейной системы не получается вовсе пи при каких значениях ее параметров, то согласно геометрическому способу определения автоколебаний (см. выше) получим, что кривая Михайлова будет либо охватывать начало координат при всяком значении а, либо не охватывать его при всех а. Отсюда можно сделать вывод, что в первом случае данная нелинейная система устойчива, а во втором — неустойчива.
Развитие, а также сравнение данного способа определения устойчивости равновесия нелинейной системы с методом Ляпунова, показывающее эффективность такого способа, см. в книге [72, §§ 2.7-2.9].
 Примеры исследования нелинейных систем первого класса Примеры исследования нелинейных систем первого класса
Рассмотрим несколько примеров применения изложенного в предыдущем параграфе метода.
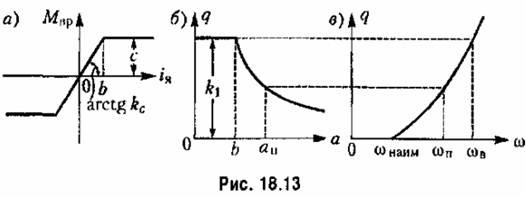
Пример 1. Найдем влияние ограничения линейной характеристики двигателя (рис. 18.13, а) на процессы в следящей системе. Пусть остальные звенья системы линейны. Тогда уравнение управляемого объекта с двигателем вместо (16.63) примет вид
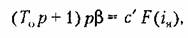
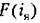 определяется графиком рис. 18.13,а. определяется графиком рис. 18.13,а.
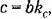 получаем уравнение управляемого объекта с двигателем в виде получаем уравнение управляемого объекта с двигателем в виде
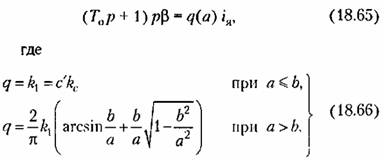
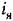 . .
Общее уравнение остальной части следящей системы согласно (16.53) будет
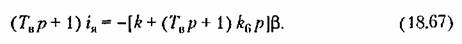
На основании (18.65) и (18.66) получаем характеристическое уравнение
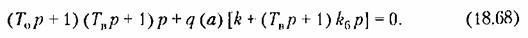
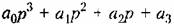 и подстановки и подстановки
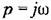 получаем уравнения типа (18.36) в виде получаем уравнения типа (18.36) в виде
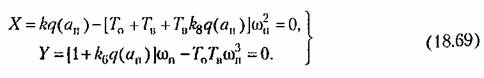
Выясним влияние параметра к на автоколебания в данной системе. Из последнего уравнения находим

 а из первого а из первого
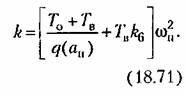
Формула (18.70) дает график, изображенный па рис. 18.13, , где
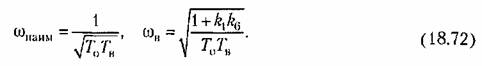
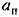 и частотой периодического решения в данной системе. и частотой периодического решения в данной системе.
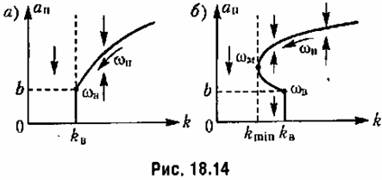
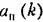 типа рис. 18.14, а типа рис. 18.14, а
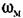 в виде в виде

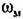 в (18.70) и (18.71), а именно: в (18.70) и (18.71), а именно:

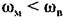 — второй (рис. 18.14, б). Сравнивая (18.73) и (18.72), приходим к выводу, что для системы, параметры которой удовлетворяют условию — второй (рис. 18.14, б). Сравнивая (18.73) и (18.72), приходим к выводу, что для системы, параметры которой удовлетворяют условию
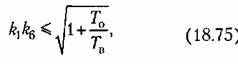 ) )
справедлив график на рис. 18.14, а, а для системы с параметрами
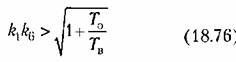
— на рис. 18.14,6.
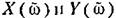 совпадают с (18.69). совпадают с (18.69).
Найдем производные:
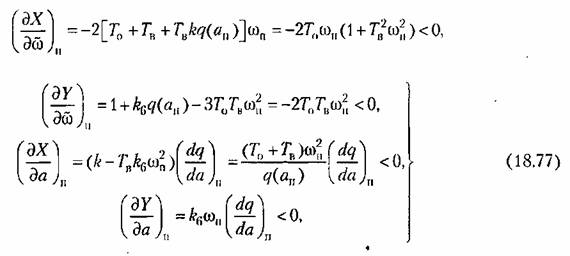
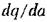 отрицательна. отрицательна.
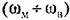 — неустойчивым. — неустойчивым.
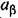 автоколебаний управляемой величины (3, надо воспользоваться уравнением (18.65), откуда автоколебаний управляемой величины (3, надо воспользоваться уравнением (18.65), откуда
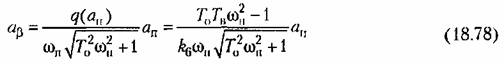
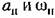 определяются графиком рис. 18.14, а или б. определяются графиком рис. 18.14, а или б.
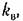 отмеченную на рис. 18.14: отмеченную на рис. 18.14:
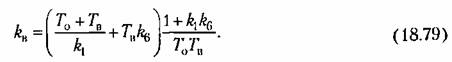
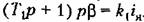 . Отсюда можно сделать вывод о том, что в случае (18.75), для которого имеет место график рис. 18.14, а, данная нелинейная система сохраняет устойчивость в той же области, что и линейная система, по она обладает еще установившимся автоколебательным режимом там, где линейная система неустойчива. . Отсюда можно сделать вывод о том, что в случае (18.75), для которого имеет место график рис. 18.14, а, данная нелинейная система сохраняет устойчивость в той же области, что и линейная система, по она обладает еще установившимся автоколебательным режимом там, где линейная система неустойчива.
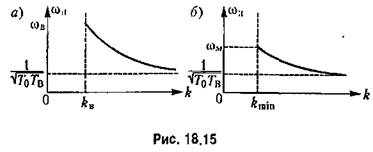
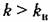 в линейной системе. Это наблюдается и на практике. в линейной системе. Это наблюдается и на практике.
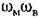 ) сохраняется еще устойчивость равновесного состояния. ) сохраняется еще устойчивость равновесного состояния.
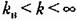 — один. — один.
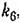 который, по существу, является коэффициентом гибкой обратной связи. При отсутствии такой связи указанное явление не имело бы места. который, по существу, является коэффициентом гибкой обратной связи. При отсутствии такой связи указанное явление не имело бы места.
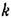 соответственно для случаев, изображенных на рис. 18.14, а и б. соответственно для случаев, изображенных на рис. 18.14, а и б.
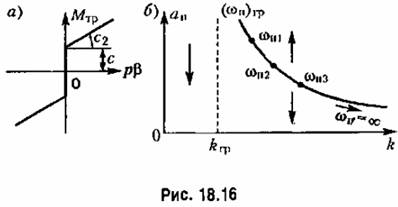
П р и м е р 2. Рассмотрим теперь следящую систему с линейной характеристикой привода, но учтем сухое трение совместно с линейным (рис. 18.16, а). Уравнение управляемого объекта с двигателем имеет при этом вид (16.52). Здесь возможны два случая: 1) колебания без остановок, когда обеспечиваются условия первого из уравнений (16.52); 2) колебания с остановками, когда действуют попеременно оба уравнения (16.52). Рассмотрим первый случай и определим условия его существования.
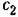 в виде в виде
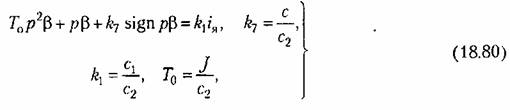
с условием, что
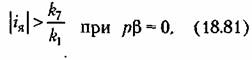
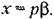 Тогда это уравнение будет Тогда это уравнение будет
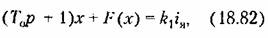
где

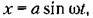 получаем получаем

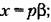 амплитуда колебаний самого угла (3 при этом, очевидно, будет амплитуда колебаний самого угла (3 при этом, очевидно, будет
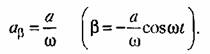
Выражение (18.84) представляет собой известную формулу линеаризации сухого трения с помощью вибраций. Найдем условия, при которых она здесь справедлива. Согласно (18.81) и (18.82) имеем

что и является условием, при котором справедливо дальнейшее решение.
Характеристическое уравнение всей замкнутой системы согласно (18.82), (18.84) и (16.53) получает вид
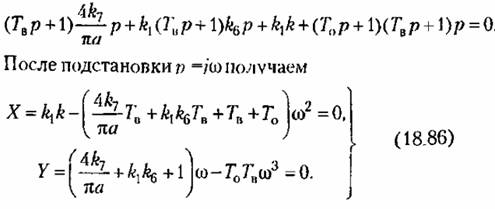
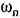 : :
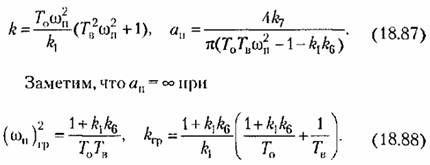
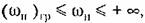 строим по формулам (18.87) график строим по формулам (18.87) график
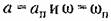 из (18.87), приводим его к виду из (18.87), приводим его к виду
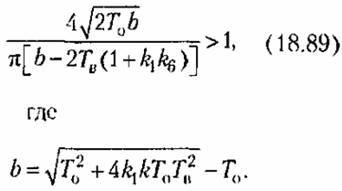
Для исследования устойчивости найденного периодического решения на основании (18.86) находим
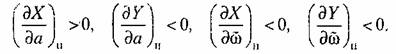
Критерий (18.63) при этом не выполняется, что означает неустойчивость найденного периодического решения. Это и показано условно вертикальными стрелками на рис. 18.16,5.
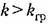 и при выполнении условия (18.89) система может быть устойчивой в малом (при начальных условиях, которые дают начальную амплитуду собственных колебаний системы в переходном процессе, лежащую ниже кривой на рис. 18.16,5). Однако система неустойчива в большом (при начальных амплитудах собственных колебаний выше этой кривой). Последнее можно объяснить физически тем, что при больших амплитудах и соответственно при больших скоростях движения демпфирующее влияние силы сухого трения, которая сохраняет одну и ту же величину при любой скорости, становится несущественным, вследствие чего система оказывается неустойчивой, как и при отсутствии сухого трения. и при выполнении условия (18.89) система может быть устойчивой в малом (при начальных условиях, которые дают начальную амплитуду собственных колебаний системы в переходном процессе, лежащую ниже кривой на рис. 18.16,5). Однако система неустойчива в большом (при начальных амплитудах собственных колебаний выше этой кривой). Последнее можно объяснить физически тем, что при больших амплитудах и соответственно при больших скоростях движения демпфирующее влияние силы сухого трения, которая сохраняет одну и ту же величину при любой скорости, становится несущественным, вследствие чего система оказывается неустойчивой, как и при отсутствии сухого трения.
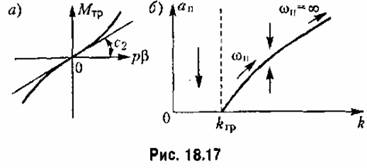
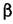 ). При этом колебания угла |3 будут происходить с остановками. Это — задача более сложная. ). При этом колебания угла |3 будут происходить с остановками. Это — задача более сложная.
Пример 3. Пусть теперь в той же системе действует не сухое трение, а сопротивление движению объекта, пропорциональное квадрату скорости, с линейной составляющей (рис. 18.17, а). Уравнение управляемого объекта с двигателем имеет в этом случае вид (16.63). Перепишем здесь его иначе по аналогии с предыдущим примером:
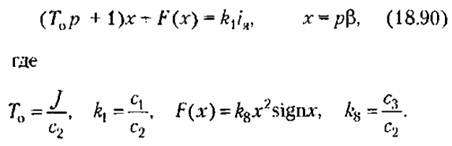
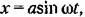 по формулам гармонической линеаризации (18.10) получаем по формулам гармонической линеаризации (18.10) получаем
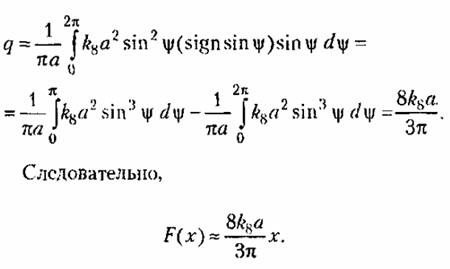
Составив, как и раньше, характеристическое уравнение, приходим к выражениям:
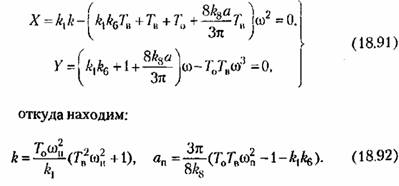
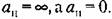 В результате получаем график для определения амплитуды и частоты периодического решения, изображенный на рис. 18.17, б. В результате получаем график для определения амплитуды и частоты периодического решения, изображенный на рис. 18.17, б.
Поскольку здесь
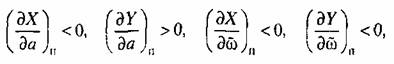
то критерий (18.63) выполняется. Поэтому найденное периодическое решение устойчиво. Следовательно, квадратичное трение приводит к автоколебаниям в той области параметров, где система без этого добавочного трения была бы неустойчивой. Это объясняется усилением демпфирующего действия квадратичной силы трения при увеличении амплитуды (и скорости) колебаний, что препятствует неограниченному раскачиванию системы. Заметим, что переход закона сопротивления движению объекта от линейного к квадратичному при больших скоростях отражает реальные явления.
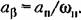
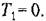
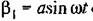 согласно формуле (18.30) принимает вид согласно формуле (18.30) принимает вид

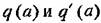 определяются по формулам (18.27), в которых надо считать к= (так как характеристика рис. 16.20, б имеет наклон 45°), а именно: определяются по формулам (18.27), в которых надо считать к= (так как характеристика рис. 16.20, б имеет наклон 45°), а именно:
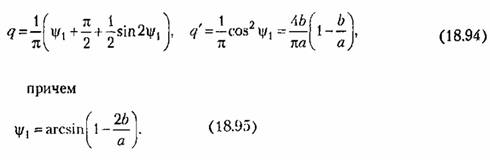
I Вторую нелинейность (16.54)
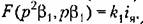
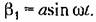
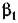 и (3 показана на рис. 18.18. При этом из нижнего графика и из формул (16.54) видно, что и (3 показана на рис. 18.18. При этом из нижнего графика и из формул (16.54) видно, что

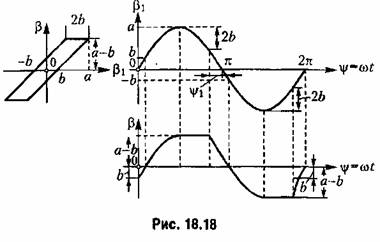
при

Условие отсутствия постоянной составляющей здесь выполняется, а третья из формул (18.11) принимает вид
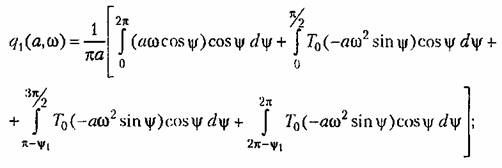
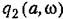 . Произведя интегрирование и сравнив результаты . Произведя интегрирование и сравнив результаты
с выражениями (18.94), получаем
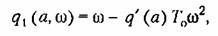
 то же, что в формулах (18.94). то же, что в формулах (18.94).
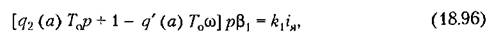
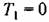 имеем имеем
 где где

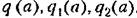
На основании (18.93), (18.96) и линейной части (16.53) приходим к характеристическому уравнению

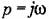 получим получим
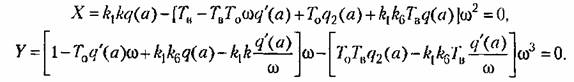
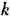 из каждого уравнения по отдельности: из каждого уравнения по отдельности:
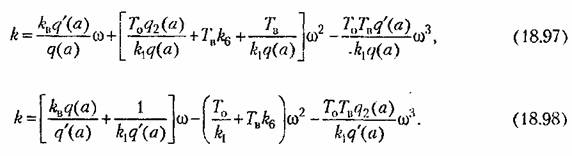
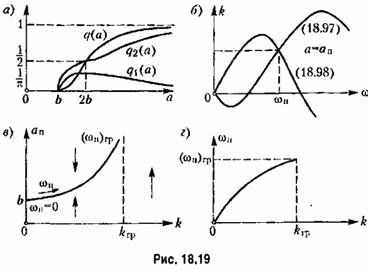
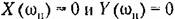 находим: находим:
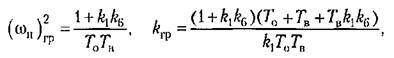
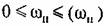
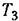 ): ):
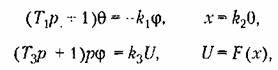
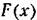 — характеристика — характеристика
реле, изображенная парне. 18.20,а.
В следующем примере произведем также учет не гистерезиспого, а временного запаздывания реле.
Гармоническая линеаризация характеристики реле рис. 18.20, а согласно формулам (18.9) и (18.15) дает
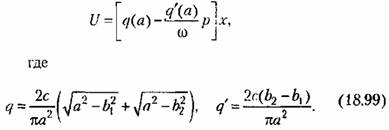
На основании написанных уравнений получаем следующее характеристическое уравнение данной замкнутой системы:
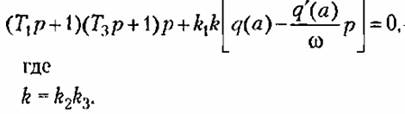
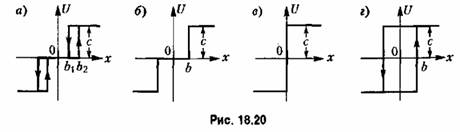
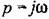 получаем выражения: получаем выражения:
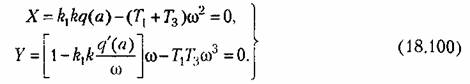
Исследуем влияние параметра к на устойчивость и автоколебания данной системы.
Из (18.100) имеем

откуда после подстановки (18.99) находим

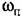 в интервале в интервале

Рассмотрим частные случаи.
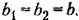 Для этого, случая Для этого, случая
из (18.99) получаем:

Поэтому второе из уравнений (18.100) дает постоянное значение частоты периодического решения

Подставляя его в первое уравнение (18.100), с учетом (18.105) находим
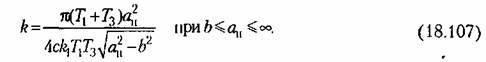
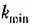 из условия равенства нулю из условия равенства нулю
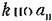 : :

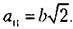
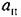 от параметра изображен на рис. 18.21, а. В этом частном случае релейной характеристики (рис. 18.20,6) для исследования устойчивости воспользуемся критерием (18.63), для которого предварительно находим от параметра изображен на рис. 18.21, а. В этом частном случае релейной характеристики (рис. 18.20,6) для исследования устойчивости воспользуемся критерием (18.63), для которого предварительно находим
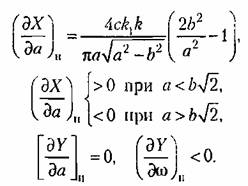
Следовательно, нижняя ветвь кривой на рис. 18.21, а соответствует неустойчивому периодическому решению, а верхняя -- устойчивому (автоколебания).
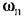 (18.106) и согласно (18.107)- прямолинейная зависимость (18.106) и согласно (18.107)- прямолинейная зависимость

изображенная на рис. 18.21, б. Здесь возможен только автоколебательный процесс; область устойчивости равновесного состояния, имевшаяся на рис. 18.21, а, пропадает.
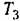 ) получается ограниченная и возникает еще область автоколебаний с большой амплитудой при одновременном существовании устойчивости в малом (рис. 18.21, а). ) получается ограниченная и возникает еще область автоколебаний с большой амплитудой при одновременном существовании устойчивости в малом (рис. 18.21, а).
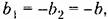 из (18.99) имеем из (18.99) имеем
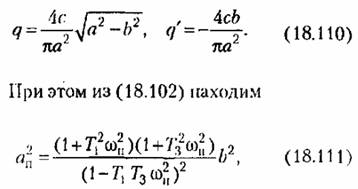
а из (18.103)
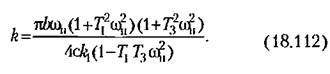
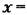
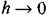 (другой способ, с дельта-функцией, см. в § 18.5, рис. 18.37). Для характеристики па рис. 18.22, а при изменении величины (другой способ, с дельта-функцией, см. в § 18.5, рис. 18.37). Для характеристики па рис. 18.22, а при изменении величины
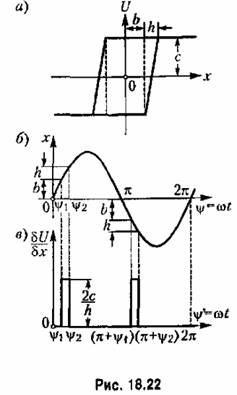
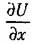 значения, показан- значения, показан-
ные на рис. 18.22, в, где
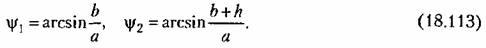
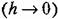 будет будет
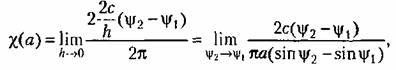
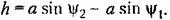
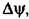
получим
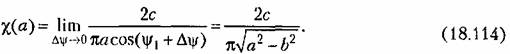
Итак, для исследования устойчивости получаем следующее характеристическое уравнение:
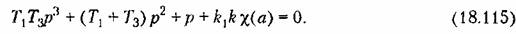
Условие устойчивости периодического решения, следовательно, по критерию Гурвица будет
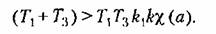
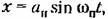 амплитуда и частота которых определяются графиками рис. 18.21, в и г или формулами (18.111), (18.112). амплитуда и частота которых определяются графиками рис. 18.21, в и г или формулами (18.111), (18.112).
Пример 6. Пусть в той же системе характеристика реле имеет простейший вид рис. 18.20, б, но имеется постоянное по времени запаздывание т. Тогда согласно (18. ПО), где Ъ = 0, уравнение нелинейного звена будет
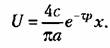
В результате получим характеристическое уравнение системы
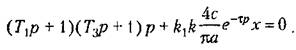
 даст два уравнения: даст два уравнения:
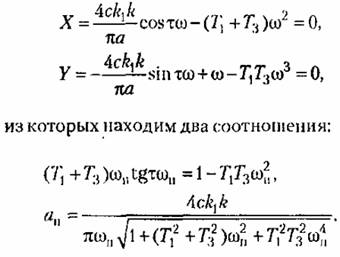
Первое из них определяет частоту (решается графически), а второе — амплитуду автоколебаний в зависимости от коэффициента усиления к и от других параметров системы.
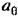 управляемой величины В (температуры) будет управляемой величины В (температуры) будет
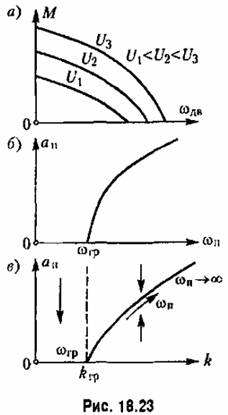
Пример 7. Рассмотрим систему автоматического управления с приводом регулирующего органа в виде двухфазного двигателя переменного тока. Характеристика этого двигателя для разных значений управляющего напряжения II имеет вид, представленный па рис. 18.23, а.
Линеаризуя характеристики, обычно считают
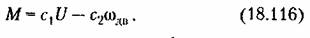 в первом приближении только для левого участка характеристики. Если же используется большая часть характеристики, то необходимо учесть ее нелинейность. Имея в виду, что на рис. 18.23, а с увеличением содв коэффициент сх уменьшается, а коэффициент с2 увеличивается, примем для описания этой характеристики вместо (18.116) следующее нелинейное выражение; в первом приближении только для левого участка характеристики. Если же используется большая часть характеристики, то необходимо учесть ее нелинейность. Имея в виду, что на рис. 18.23, а с увеличением содв коэффициент сх уменьшается, а коэффициент с2 увеличивается, примем для описания этой характеристики вместо (18.116) следующее нелинейное выражение;
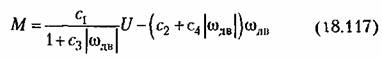 положительными). Аналогично можно положительными). Аналогично можно
подбирать и любой другой более подходящий нелинейный закон для описания характеристик двигателя.
Введем для дальнейшего обозначение

Тогда дифференциальное уравнение двигателя
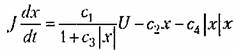
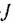 — момент инерции всех вращаемых двигателем масс, приведенных к валу двигателя) можно записать в виде — момент инерции всех вращаемых двигателем масс, приведенных к валу двигателя) можно записать в виде
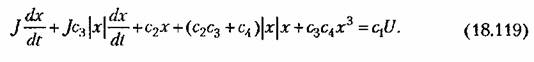
Здесь имеем три нелинейные функции:
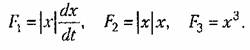
Гармоническая их линеаризация по правилам § 18.1 дает:
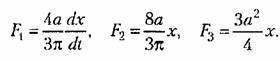
Подставляя это в (18.119), получаем следующее уравнение двухфазного двигателя (для колебательных процессов):
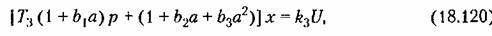 ) )
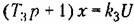 , где , где
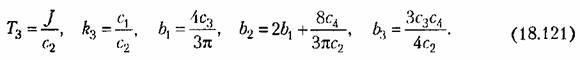

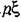 с учетом передаточного числа редуктора и с обозначением (18.118) будет с учетом передаточного числа редуктора и с обозначением (18.118) будет

Уравнение объекта и уравнение чувствительного элемента возьмем соответственно в виде

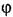 — отклонение управляемой величины. — отклонение управляемой величины.
Характеристическое
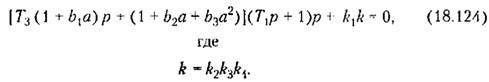
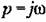 получаем: получаем:
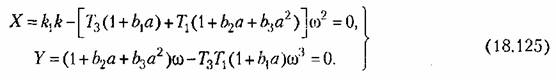
Рассмотрим при этом влияние параметра к. Второе из уравнений (18.125) дает
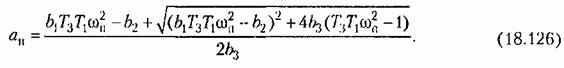
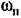 искомого периодического решения в виде (рафика, показанного на рис. 18.23, б, где искомого периодического решения в виде (рафика, показанного на рис. 18.23, б, где

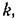 влияние которого рассматривается: влияние которого рассматривается:
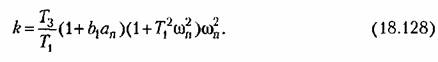
Поэтой формуле, используя предыдущие результаты, получаем график зависимости амплитуды автоколебаний аи от величины параметра к, показанный на рис. 18.23, в.
|