Теория систем автоматического управленияСтационарные случайные процессы


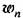 не меняются при любом сдвиге рассматриваемого участка процесса во времени, т. е. при сохранении постоянной разности. не меняются при любом сдвиге рассматриваемого участка процесса во времени, т. е. при сохранении постоянной разности.
Можно сказать, что стационарный случайный процесс в какой-то мере аналогичен обычным стационарным или установившимся процессам в автоматических системах. Например, при рассмотрении обычных установившихся периодических колебаний ничего не изменится, если перенести начало отсчета на какую-нибудь величину. При этом сохранят свои значения такие характеристики, как частота, амплитуда, среднеквадратичное значение и т. п.

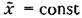 (рис. 11.13), подобно постоянному (рис. 11.13), подобно постоянному
смещению средней линии обычных периодических колебаний. Рассеяние значений переменной х в стационарном случайном процессе, определяемое а = сопз1, также будет все время одинаковым, подобно постоянному значению среднеквадратичного отклонения обычных установившихся колебаний от средней линии.
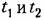 (рис. 11.13), т. е. (рис. 11.13), т. е.
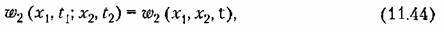
и также для n-мерной плотности вероятности.
Задание всех этих функций распределения плотности определяет случайный процесс. Однако более удобно иметь дело с некоторыми осреднепными и характеристиками процесса.
Прежде чем перейти к ним, отметим два важных для практики свойства.
1. Ограничиваясь только стационарными случайными процессами, можно бу дет определить только установившиеся (стационарные) динамические ошибки автоматических систем при случайных воздействиях. Такой прием применялся и ра нее при рассмотрении регулярных воздействий, когда определялись динамические свойства систем по величине динамических ошибок в установившемся периодическом режиме.
2. Стационарные случайные процессы обладают замечательным свойством, ко торое известно под названием эргодической гипотезы.
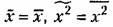 и т. д. и т. д.
 то длительное наблюдение случайного процесса на одном объекте (среднее по времени) дает в среднем такую же картину, как и большое число наблюдений, сделанное в один и тот же момент времени на большом числе одинаковых объектов (среднее по множеству). то длительное наблюдение случайного процесса на одном объекте (среднее по времени) дает в среднем такую же картину, как и большое число наблюдений, сделанное в один и тот же момент времени на большом числе одинаковых объектов (среднее по множеству).
Для многих случаев существует математическое доказательство этого свойства. Тогда оно сводится к эргодической теореме.
Итак, среднее значение (математическое ожидание) для стационарного процесса будет

Аналогичным образом могут быть записаны моменты более высоких порядков -дисперсия, среднеквадратичное отклонение и т. п.
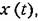 по- по-
лученной при испытании одной системы в течение длительного времени вместо параллельного Испытания многих однотипных систем в один и тот же момент времени.
Таким образом, важное свойство стационарного случайного процесса состоит в том, что отдельная его реализация на бесконечном промежутке времени полностью определяет собой весь случайный процесс со всеми бесчисленными возможными его реализациями. Этим свойством не обладает никакой другой тип случайного процесса.
|