Теория систем автоматического управленияМногомерные системы управления
 . Это имеет место во многих современных сложных системах. К ним относятся, например, системы стабилизации напряжения и частоты синхронных генераторов, системы управления подвижных объектов, многие системы управления технологическими процессами и др. . Это имеет место во многих современных сложных системах. К ним относятся, например, системы стабилизации напряжения и частоты синхронных генераторов, системы управления подвижных объектов, многие системы управления технологическими процессами и др.
Многомерная система предполагает наличие многомерного объекта управления (рис. 5.14), который характеризуется существованием нескольких входов (точек приложения управляющих и возмущающих воздействий) и нескольких выходов, определяемых управляемыми величинами.
Многомерный объект описывается системой уравнений, которую удобно представлять в матричной форме.
Введем одностолбцовую тимерную матрицу управляемых величин

Здесь индексом Г обозначена операция транспонирования матрицы.
Если управляемые величины имеют одинаковую физическую размерность и могут трактоваться как проекции некоторого вектора на оси координат, матрица-столбец может отождествляться с этим вектором. Тогда можно говорить*) векторе управляемых величин.
Если управляемые величины имеют разную физическую размерность, то переход от. матрицы-столбца к вектору в принципе может быть сделан и в этом случае, если ввести в матрицу-столбец весовые коэффициенты, уравнивающие размерности отдельных составляющих. Однако такой переход не является единственным, а имеет бесчисленное количество вариантов.
Аналогичным образом при равенстве физических размерностей отдельных составляющих матриц-столбцов управляющих воздействий и возмущений может быть введен вектор управления и вектор возмущения. При разных физических размерностях отдельных составляющих матриц-столбцов переход к вектору возможен, но не будет единственным.
Линеаризованные уравнения движения многомерного объекта могут быть записаны в матричном виде:

Если в выражениях (5.101) - (5.107) перейти к изображениям Лапласа при нулевых начальных условиях, то матричное уравнение (5.104) может быть записано для изображений в следующем виде:

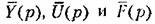 — матрицы-столбцы изображений управляемых величин, управляющих воздействий и возмущений. — матрицы-столбцы изображений управляемых величин, управляющих воздействий и возмущений.
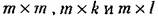 соответственно. соответственно.
 получим получим

Здесь введены матрицы передаточных функций объекта для управляющих воздействий
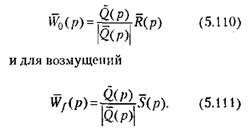
 обозначена матрица, присоединенная для матрицы обозначена матрица, присоединенная для матрицы
 Формулы (5,109)-(5,111) позволяют получить связь между управляемыми величинами и управляющими и возмущающими воздействиями. Так, например, если Формулы (5,109)-(5,111) позволяют получить связь между управляемыми величинами и управляющими и возмущающими воздействиями. Так, например, если
 то из (5.109) и (5.110) можно получить для изображений то из (5.109) и (5.110) можно получить для изображений

 которая определяет используемые алгоритмы управления. Она дает связь между изображениями управляющих воздействий и ошибок: которая определяет используемые алгоритмы управления. Она дает связь между изображениями управляющих воздействий и ошибок:
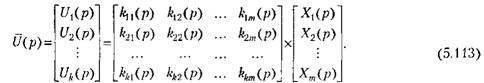
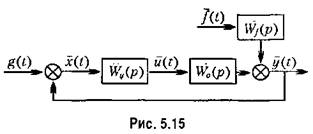
Уравнения многомерной системы (рис. 5.15) могут быть получены действиями, аналогичными одномерному случаю (§ 5.2).
Матрица передаточных функций разомкнутой но всем каналам системы
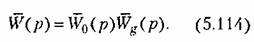

 — единичная матрица размером т х т, т. е. квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные — нулю. — единичная матрица размером т х т, т. е. квадратная матрица, у которой все элементы главной диагонали равны единице, а остальные — нулю.
Характеристическое уравнение системы получается приравниванием нулю определителя характеристической матрицы:

 В этом случае общее характеристическое В этом случае общее характеристическое
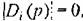

 не- не-
особая, что означает независимость исходных дифференциальных уравнений, могут быть определены из выражений
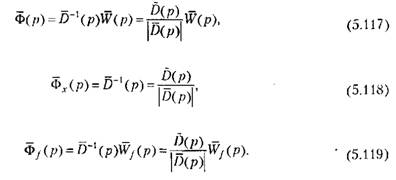
Полученные выражения для матриц передаточных функций замкнутой системы позволяют использовать формулы, аналогичные формулам § 5.2, но записанные уже для матриц-столбцов ошибок и управляемых величин. Так, например, для матрицы изображений ошибок имеем

Исходные дифференциальные уравнения многомерной системы могут быть также представлены в виде уравнений состояния:

 — матрица-столбец переменных состояния, — матрица-столбец переменных состояния,
п — порядок дифференциального уравнения.
 соответствующее системе (5.121), имеет вид соответствующее системе (5.121), имеет вид
 — единичная матрица п х п. — единичная матрица п х п.
Выбор переменных состояния для многомерных систем (в отличие от одномерных) представляет собой сложную задачу и здесь не рассматривается.
Условием полной управляемости многомерной системы является невырожденность матрицы Калмана
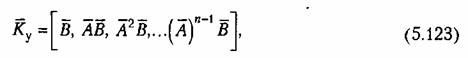
а условием полной наблюдаемости — невырожденность матрицы

Матрицы (5.93) и (5.99) представляют собой частные случаи матриц (5.123) и Критерии устойчивости
|