Теория систем автоматического управленияВынужденные колебания нелинейных систем
Симметричные одночастотные вынужденные колебания
Проблема анализа вынужденных колебаний нелинейных систем вообще является весьма сложной и многообразной. Поскольку принцип наложения решений (суперпозиция) здесь неприменим, то, вообще говоря, нельзя складывать частные решения при различных внешних воздействиях, найденных по отдельности, а также складывать свободные и вынужденные колебания. Особое нелинейное сложение решений возможно в случае, если решения разделяются по степени медленности протекания их во времени (т. е. по значению возможных частот колебаний), аналогично тому, как эта делалось в главе 19. При этом каждое из складываемых решений существенно зависело от другого, а именно амплитуда автоколебаний существенно зависела от величины смещения, характеризующей медленно протекающие процессы. Такого же рода разделение решений для вынужденных колебаний будет рассмотрено ниже, где появится возможность рассмотрения нелинейных двухчастотных колебаний с большой разностью частот.
Не касаясь сложных форм вынужденных колебаний нелинейных систем (хотя их исследование также имеет большое практическое значение), ограничимся в данном параграфе определением одночастотных вынужденных колебаний, когда колебания системы происходят с частотой внешнего периодического воздействия. Форма колебаний, как и прежде, на основании свойства фильтра будет считаться близкой к синусоидальной для переменной х, стоящей под знаком нелинейной функции. При рассмотрении вынужденных колебаний во многих случаях возникают ограничения, накладываемые на амплитуду и частоту внешнего периодического воздействия (зависящие также и от параметров системы) и обусловливающие существование одночастотных вынужденных- колебаний в нелинейной системе. Будем их кратко называть условиями захватывания (в указанном широком смысле). Особое значение эти условия приобретают для автоколебательных систем при частотах, близких к частоте автоколебаний и выше.
Итак, пусть имеется некоторая нелинейная автоматическая система, в любом месте которой приложено внешнее синусоидальное воздействие

Пусть уравнение динамики системы приведено к виду
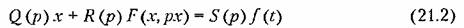
Выполнение условий фильтра (§ 18.2), а также выводимых ниже условий захватывания (где это необходимо) позволяет в первом приближении искать решение для установившихся вынужденных колебаний системы в синусоидальной форме

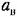 и т. п. и т. п.
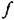 через х. Согласно (21.1) через х. Согласно (21.1)
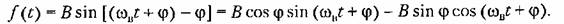
Отсюда, принимая во внимание выражение (21.3) для х и выражение для его производной
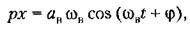
окончательно получаем
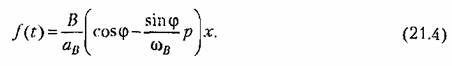
Подставив это выражение в заданное дифференциальное уравнение системы (21.2)/ получим
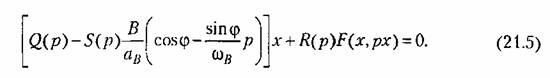
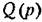 на новый операторный многочлен, стоящий в на новый операторный многочлен, стоящий в
(21.5) в квадратных скобках. Применяя при отыскании синусоидального периодического решения формально тот же метод, что и в главе 18, нужно потребовать выполнения свойства фильтра от этой новой системы.
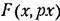 должна допускать симметричные колебания, т. е. должна допускать симметричные колебания, т. е.
должно выполняться условие
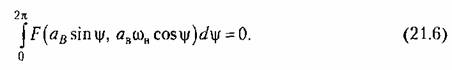
Итак, получив для определения вынужденных колебаний однородное уравнение (21.5), можно, как и в § 18.2, произвести гармоническую линеаризацию нелинейности
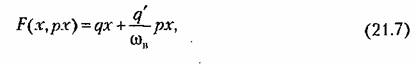
где
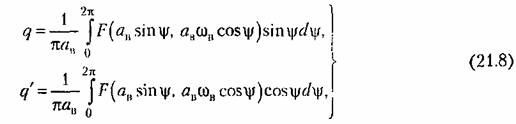
причем согласно (21.3)

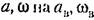
Таким образом, для каждой нелинейности в общем случае получаются зависимости

а во многих частных случаях (см. главу 18) —

В результате из (21.5) и (21.7) получаем характеристическое уравнение для первого приближения
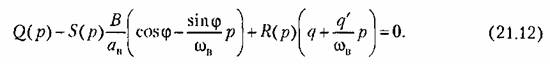
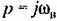 , что соответствует отысканию , что соответствует отысканию
синусоидального решения (21.3), получаем
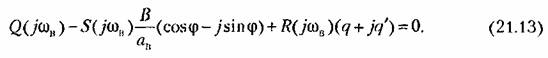
Замечая, что
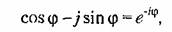
из уравнения (21.13) находим, что
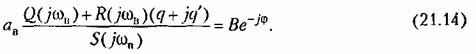
Возможны два метода дальнейшего решения задачи. Эти методы остаются справедливыми и для нелинейных систем с временным запаздыванием т, когда выражение (21.14) принимает вид
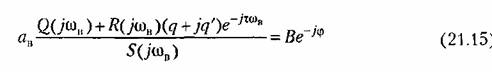 > >
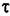 . .
Графический метод. Для каждого значения частоты при заданных параметрах системы на комплексной плоскости строится кривая (рис. 21.1)
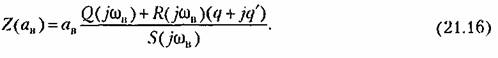
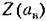 — величина амплитуды ав вынужденных колебаний. — величина амплитуды ав вынужденных колебаний.
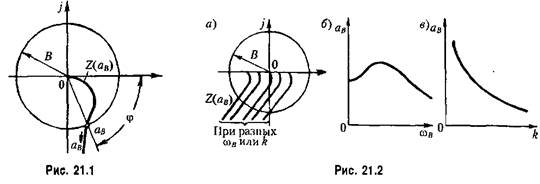
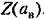
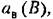 напри- напри-
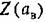
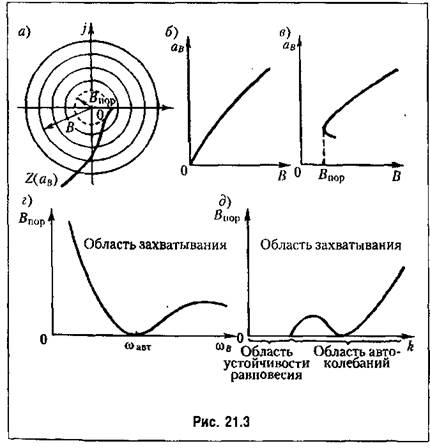
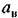 (В) тина рис. 21.3, е. (В) тина рис. 21.3, е.
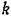 . .
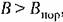 , наблюдается чаще , наблюдается чаще
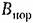 равно нулю обычно также в области отсутствия автоколебаний (область устойчивости равновесия системы, рис. 21.3, д). равно нулю обычно также в области отсутствия автоколебаний (область устойчивости равновесия системы, рис. 21.3, д).
 (область захватывания), а при значениях, лежащих ниже кривой, будет иметь место более сложное вынужденное движение системы. Это и является определением (пока графическим) условий захватывания, о которых говорилось выше. (область захватывания), а при значениях, лежащих ниже кривой, будет иметь место более сложное вынужденное движение системы. Это и является определением (пока графическим) условий захватывания, о которых говорилось выше.
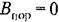 , как в случае рис. 21.3,6. , как в случае рис. 21.3,6.
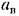 и сдвига фазы фодиочастотных вынужденных колебаний нелинейной системы. Для этого выделим вещественные и мнимые части числителя и знаменателя и запишем равенства для модулей и аргументов обеих частей уравнения (21.14) или (21.15): и сдвига фазы фодиочастотных вынужденных колебаний нелинейной системы. Для этого выделим вещественные и мнимые части числителя и знаменателя и запишем равенства для модулей и аргументов обеих частей уравнения (21.14) или (21.15):
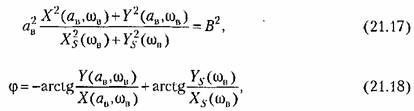
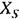
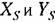 являются новыми выражениями, соответствующими правой части являются новыми выражениями, соответствующими правой части
заданного нелинейного уравнения (21.2).
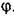
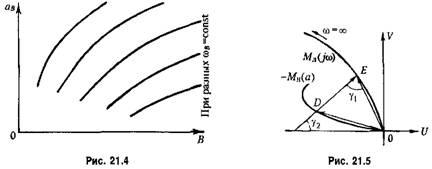
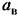 и вычислять каждый раз величину В. По результатам этих вычислений легко строится график (рис. 21.4), который и представляет собой искомое решение уравнения (21.17). и вычислять каждый раз величину В. По результатам этих вычислений легко строится график (рис. 21.4), который и представляет собой искомое решение уравнения (21.17).
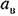 в уравнении (21.17). Это условие автоматически выявится при построении графика типа рис. 21.4. в уравнении (21.17). Это условие автоматически выявится при построении графика типа рис. 21.4.
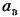 и сдвиг фазы ф вынужденных колебаний для переменной х, стоящей под знаком нелинейной функции. После этого можно подсчитать амплитуду и фазу первой гармоники вынужденных колебаний для любой другой переменной исследуемой системы на основании соответствующих уравнений или передаточных функций звеньев, связывающих эту переменную с переменной х. и сдвиг фазы ф вынужденных колебаний для переменной х, стоящей под знаком нелинейной функции. После этого можно подсчитать амплитуду и фазу первой гармоники вынужденных колебаний для любой другой переменной исследуемой системы на основании соответствующих уравнений или передаточных функций звеньев, связывающих эту переменную с переменной х.
Частотный метод. Пустъ нелинейное звено в системе определяется уравнением

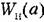 I I
согласно формулам (18.210) и (18.211). Рассмотрим два случая,
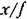 , замкнутой системы такова, что , замкнутой системы такова, что
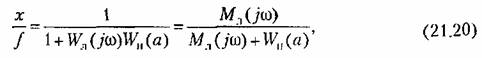
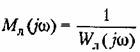 — обратная амплитудно-фазовая характеристика линейной части. — обратная амплитудно-фазовая характеристика линейной части.
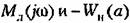 на комплексной плоскости (рис. 21.5). на комплексной плоскости (рис. 21.5).
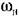 точку Е. Из формулы (21.20) и из чертежа (рис. 21.5) находим точку Е. Из формулы (21.20) и из чертежа (рис. 21.5) находим
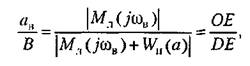
откуда амплитуда В внешнего периодического воздействия/получает значение

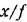 замкнутой системы такова, что замкнутой системы такова, что
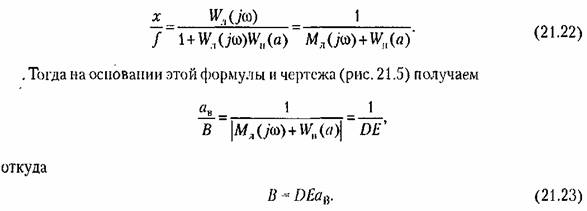
В других случаях, когда передаточная функция не подходит под частные виды (21.20) и (21.22), построения усложняются.
|