Построение высоконадежных системОценка надежности по малой информации
на примере стареющих распределений. Иногда специалисту по надежности, которому предстоит рассчитать вероятностные характеристики проектируемой системы, бывает известна лишь ограниченная статистика о надежности используемых элементов. (Напомним, что под элементом в широком смысле слова понимается любая часть системы, включая и очень большие подсистемы.) Малая статистика позволяет говорить более или менее достоверно лишь об оценках среднего времени безотказной работы и в лучшем случае об оценках для дисперсии распределения времени безотказной работы элемента. Если мы знаем лишь среднее время безотказной работы, то, как известно, из этого факта невозможно получить никакой нетривиальной информации о самом виде распределения времени безотказной работы. Если нам известна дополнительно еще дисперсия распределения, то мы можем для произвольного распределения записать известную оценку Чебышева:
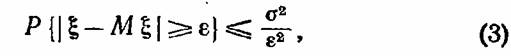
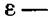 произвольная положительная величина. произвольная положительная величина.
 эта граница тривиальна. Естественно ожидать сужения этих границ для оценки неизвестной функции распределения, если нам известна какая-либо дополнительная информация. эта граница тривиальна. Естественно ожидать сужения этих границ для оценки неизвестной функции распределения, если нам известна какая-либо дополнительная информация.
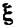 является стареющей. Старение является достаточно понятным и естественным свойством. Оно означает, что вероятностные характеристики надежности некоторого изделия ухудшаются с течением времени. Например, старение некоторого изделия может означать возрастание с течением времени интенсивности отказов либо убывание среднего значения остаточного времени жизни в зависимости от длительности уже прожитой жизни. (Справедливости ради следует заметить, что эта совершенно качественная на первый взгляд информация приводит к появлению вполне строгих математических условий. Так, для стареющих случайных величин могут быть определены соответствующие ограничения на все моменты распределения.) является стареющей. Старение является достаточно понятным и естественным свойством. Оно означает, что вероятностные характеристики надежности некоторого изделия ухудшаются с течением времени. Например, старение некоторого изделия может означать возрастание с течением времени интенсивности отказов либо убывание среднего значения остаточного времени жизни в зависимости от длительности уже прожитой жизни. (Справедливости ради следует заметить, что эта совершенно качественная на первый взгляд информация приводит к появлению вполне строгих математических условий. Так, для стареющих случайных величин могут быть определены соответствующие ограничения на все моменты распределения.)
Зачастую суждение о том, является ли данное распределение стареющим или нет, можно сделать и без каких-либо конкретных статистических данных — просто на основании априорных недостаточно общих соображений. Например, если отказ элемента возникает в результате определенного накопления дефектов до некоторого критического уровня, то предположение о старении является вполне естественным: чем больше проходит времени с момента начала работы, тем с большей вероятностью возникновение очередного дефекта может привести к превышению этого критического уровня.
Вообще говоря, различные типы старения, о которых говорилось ранее, отличаются по своим свойствам. Поэтому для определенности будем говорить лишь о старении, характеризуемом возрастанием интенсивности отказов.
Напомним, что интенсивность отказов есть функция, определяемая как условная плотность распределения вида
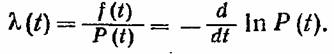
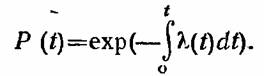
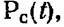 соответствующая стареющей случайной величине, пересекает произвольную экспоненту самое большее один раз, причем сверху, если такое пересечение имеет место. Из определения среднего времени безотказной работы соответствующая стареющей случайной величине, пересекает произвольную экспоненту самое большее один раз, причем сверху, если такое пересечение имеет место. Из определения среднего времени безотказной работы


В свою очередь, этот факт позволяет, далее, получить целую серию интереснейших результатов. Так, удается показать, что для стареющих распределений коэффициент вариации, т. е. отношение дисперсии к квадрату среднего значения, не превышает единицы. Другими словами, накладывается строгое условие на дисперсию.
Далее, для стареющего распределения, у которого известно лишь среднее значение, удается получить достаточно содержательные двусторонние границы для неизвестной функции вероятности безотказной работы:

Оценки (5) и (6) тривиальны и поэтому не требуют объяснения.
 и построим усеченную справа в этой точке экспоненту и построим усеченную справа в этой точке экспоненту

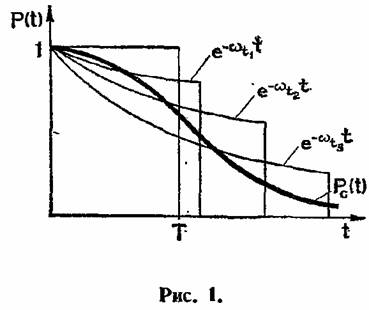

так как в противном случае нарушалось бы условие равенства средних значений рассматриваемого стареющего распределения и усеченного экспоненциального распределения (рис. 1). Неравенство (8) и приводит к оценке (7). Таким образом, на ранней стадии оценки надежности, когда мы не располагаем никакими достоверными данными о функции распределения времени безотказной работы, кроме среднего значения и общих соображений о возможном характере старения, мы можем все же получить достаточно хорошие двусторонние оценки значений вероятности безотказной работы для заданных интервалов времени.
Заметим, что если нам дополнительно известна дисперсия неизвестного стареющего распределения, то могут быть получены гораздо более точные двусторонние оценки. (Подробнее об этом можно прочитать в книге [2].)
Симметризация структуры в математической модели (на примере ветвящихся систем). Иногда на ранних этапах проектирования бывает известен лишь общий принцип построения системы и основные показатели ее выходного эффекта. Например, может возникнуть.з адача спроектировать централизованную систему управления некоторыми исполнительными (или.выходными ) элементами. Управление предполагается в соответствии со строгой иерархией подчиненности, причем исполнительный элемент системы считается функционирующим нормально, если он не только сам исправен, но и имеет связь с основным (центральным) управляющим элементом (рис. 2)
Точная конфигурация системы на раннем этапе проектирования может быть неизвестна, а известно лишь, что
элемент каждого " ранга может управлять определенным числом элементов последнего, п-го ранга, и что всего в системе может быть не более некоторого заданного числа исполнительных элементов. Требуется оценить


При такой постановке задачи заниматься прямым перебором всех возможных вариантов построения системы, а затем пытаться анализировать различные достаточно сложные частные структуры вряд ли представляется целесообразным. Более естественным будет изучить аналитически несколько типовых структур, симметризованных в целях получения компактного аналитического результата.
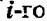 ранга. Всю структуру будем предполагать симметричной и изотропной по рангам. ранга. Всю структуру будем предполагать симметричной и изотропной по рангам.
 указанной постановке остается еще сформулировать, что же имеет смысл понимать под эффективностью функционирования. В соответствии с [111 назовем эффективностью функционирования системы математическое ожидание ее выходного эффекта. Итак, в нашем случае эффективность может быть определена как указанной постановке остается еще сформулировать, что же имеет смысл понимать под эффективностью функционирования. В соответствии с [111 назовем эффективностью функционирования системы математическое ожидание ее выходного эффекта. Итак, в нашем случае эффективность может быть определена как
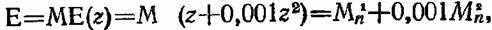 виде: виде:

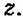 Мы будем исследовать только две структуры: Мы будем исследовать только две структуры:
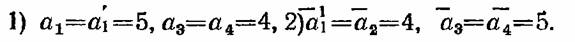
(Понятно, что они в определенном. с мысле являются граничными.)
Однако сначала вкратце покажем принцип исследования подобного рода иерархических структур.
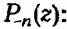


 элементов наступит отказ. элементов наступит отказ.
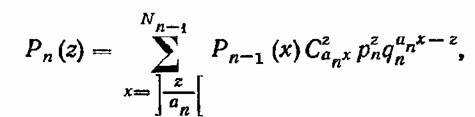
а затем для моментной производящей функции имеем

После перемены порядка суммирования и ряда несложных преобразований получаем окончательно рекуррентную формулу

которая позволяет записать затем следующие рекуррентные выражения для двух первых начальных моментов
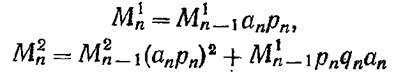
или окончательно в замкнутой форме
Теперь

перейдем к анализу наших структур.
Из формулы (9) видно, что характер структуры не влияет на величину первого момента. Для обоих случаев он численно равен
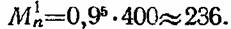
 получаем в первом случае значение получаем в первом случае значение

а во втором случае —

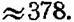
Таким образом, можно сделать вывод, что при подобного рода критерии эффективности желательно строить структуру системы так, чтобы на верхних рангах управления коэффициенты разветвления были больше. (Конечно, этот вывод может оказаться принципиально неверным для другой ситуации, когда большой коэффициент разветвления на высших рангах может быть вредным из-за появления нежелательных последствий децентрализации.)
|