Надежность и проектирование технических систем

Количественные характеристики надежности технических изделий существенно важны на трех основных этапах разработки системы: задание требований (норм), априорный расчет ожидаемых характеристик при проектировании, экспериментальная оценка характеристик в процессе испытаний и эксплуатации.

После составления и утверждения технического задания на проектируемую систему, куда непременной составной частью входят и требования по надежности функционирования, разработчики приступают непосредственно к проектированию системы. Проектирование начинается с составления относительно грубого эскиза будущей системы, выяснения возможных принципов ее функционирования и поисков рационального пути реализации возникающих идей на практике. Естественно, что принятие обоснованного решения не может опираться лишь на чисто качественные и совершенно интуитивные соображения конструкторов системы, хотя опытный конструктор и без проведения количественных оценок дает, как правило, достаточно хорошие варианты решений, основываясь на опыте предыдущих разработок. Однако в связи с бурным развитием техники и созданием новых систем, которые не имели прежде аналогов. в озникает необходимость проведения количественных оценок для сравнения альтернативных вариантов и выбора среди них в каком-то смысле наилучшего.

Специфика расчетных работ по надежности, проводимых на этапе проектирования, позволяет использовать довольно разнообразный арсенал аналитических и алгоритмических средств современной математики, в первую очередь вероятностно-статистических методов. Мы попытаемся дать несколько интересных примеров для иллюстрации этого утверждения.

Приближенная оценка надежности с использованием экспоненциальной модели. Довольно часто оказывается, что уже известна структура системы и имеются вполне достоверные статистические данные о различных необходимых характеристиках функционирования, например, о распределении времени безотказной работы, о распределении времени восстановления отказавших элементов, о существующих возможностях проведения ремонта отказавших элементов и т. п. Однако математическая модель рассматриваемого объекта может оказаться настолько сложной, что аналитического ее решения нет и оно даже не может быть получено в строгой форме, а статистическое моделирование с использованием электронных вычислительных машин требует недопустимо большого времени. Более того, следует специально подчеркнуть, что проведение тонких и трудоемких математических расчетов на этапе предварительной оценки даже и не является оправданным.

В этом случае приходится прибегать к двум основным приемам: либо заменять точную математическую модель приближенной, в которой например, произвольные функции распределения являются экспоненциальными (т. е. математическая модель объекта сводится к марковской модели, для которой хорошо известны методы решения, или же имеются готовые результаты в относительно компактной замкнутой форме), либо использовать асимптотические модели, в которых делается предположение об определенных соотношениях между теми или иными параметрами системы.

элементов. Из этих элементов

  элементов находятся в режиме облегченного резерва, т. е., находясь в резервном состоянии, они в меньшей степени подвержены отказам, чем основные элементы или резервные, находящиеся под нагрузкой.

Предполагается, что система построена так, что при отказе любого основного элемента на его место может встать любой элемент из нагруженного резерва, а место последнего, занимает сразу же один из элементов, находящийся в облегченном, резерве. Аналогичным образом и при отказе нагруженного резервного элемента на его место встает элемент из облегченного резерва. Любой из отказавших элементов поступает на ремонт, который продолжается в течение случайного времени, зависящего от конкретных факторов (длительность непрерывной работы, после которой наступил отказ, режим работы, в котором находился элемент в момент отказа, и т. п ). Предположим, что одновременно может ремонтироваться не более двух отказавших элементов, т. е. при большем числе отказов наблюдается очередь на ремонт.

относятся к одному и тому же классу. В этих условиях разумно сделать следующие предположения. На основании известных распределений вычисляем-средние значения и дисперсии:

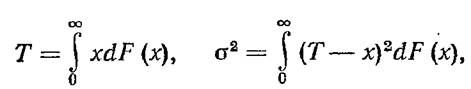
Если при этом оказывается, что коэффициенты вариации этих распределений сравнительно близки к единице, т. е.

, является достаточно правдоподобной. (Напомним, что экспоненциальное распределение характеризуется коэффициентом вариации, равным единице.)

Далее, для экспоненциального распределения характерно отсутствие последействия, т. е., сделав допущение о приемлемости этого распределения, мы тем самым снимаем вопрос о виде условного распределения времени работы для элемента, проработавшего некоторое время в облегченном режиме перед переходом в нагруженный режим.

— коэффициент нагрузки, прини -

Теперь нетрудно строго сформулировать марковскую модель для рассматриваемой восстанавливаемой системы, решение которой не представляет трудностей, а полученные результаты, как можно ожидать, будут достаточно приемлемыми для ориентировочных оценок.

и запишем для него следующее

уравнение, описывающее полную группу событий:

Нетрудно записать выражения для условных вероятностей перехода:

  получаем дифферен -

циальное уравнение вида

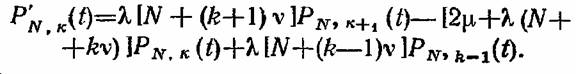система дифференциальных уравнений, описывающая функционирование рассматриваемой системы, имеет вид

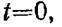  в системе нет ни одного отказавшего элемента (возможны и другие начальные условия). Эта система уравнений известна под названием схемы гибели и размножения.

элементов.

Решение полученной линейной системы алгебраических уравнений, соответствующей схеме гибели и размножения, хорошо известно в теории массового обслуживания я в теории надежности [3], [4],

В нашей системе состояниями работоспособности являются состояния

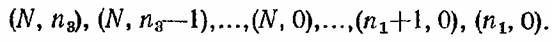
Следовательно, коэффициент готовности равняется сумме вероятностей пребывания во всех этих состояниях, т. е.

Заметим, что при довольно общих предположениях ряд показателей надежности, вычисленных в предположении об экспонеициальности распределений, совпадает с показателями, вычисленными для общего случая, а некоторые могут быть использованы как приемлемые для практических целей оценки.