Паровые турбины. Часть 1Течение пара в турбинных решетках
ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СЖИМАЕМОЙ ЖИДКОСТИ
Преобразование энергии в ступени турбины происходит в результате обтекания паровым потоком сопловых неподвижных и рабочих вращающихся лопаток турбины. В потоке возникают потери, которые снижают КПД турбины. Задачей инженера, проектирующего турбину, является такая организация потока, при ко юрой потери имеют наименьшую величину и тем самым обеспечивается высокий КПД турбины. Законы течения сжимаемой жидкости имеют большое значение для изучения тепловых процессов турбины, и они подробно излагаются в курсах газовой динамики.
В настоящей главе представлены некоторые основные уравнения, необходимые для теплового расчета турбины — определения ее размеров, КПД, а также для оценки явлений, возникающих в процессе изготовления и эксплуатации турбины. Чтобы получить достаточно простые формулы, применимые при инженерных расчетах, приходится вводить ряд упрощающих предположений. В частности рассматривается установившийся поток пара, т. е. предполагается, что параметры потока в любой точке сохраняются неизменными во времени и что их изменение возникает только при переходе от одного сечения к другому. Такое предположение не является точным.
В действительности в турбинной ступени поток подвергается периодическому возмущению —вращающиеся рабочие лопатки попеременно то проходят мимо центральной части сопловых каналов, то пересекают след, образующийся за выходными кромками предыдущих лопаток. Таким образом, турбинная решетка обтекается потоком с периодически меняющимися параметрами — скоростью, ее направлением; меняется и усилие, создаваемое паром. В первом приближении предполагается, что процесс является установившимся, а искажающий эту картину течения эффект, вызванный такой периодической нестационарностью, учитывается отдельно. Условие стационарности не соблюдается также при колебаниях параметров и быстром изменении нагрузки турбины.
Для многих практических задач, которые приходится решать при расчете турбины, можно использовать уравнения одномерного течения, выведенные в предположении, что изменения параметров и скорости потока в канале происходят в одном направлении. В ряде случаев (см., например, § 2.4 и 3.4) необходимо рассматривать двух-, а иногда и трехмерный ноток в ступени.
Там, где теоретический анализ пока не обеспечивает надежного определения истинного характера течения, на помощь приходит эксперимент, позволяющий сочетать упрощенный математический аппарат с экспериментальными коэффициентами и получать, таким образом, достаточно достоверный результат.
Для расчетов течения сжимаемой жидкости в дальнейшем используются следующие уравнения: уравнение состояния; уравнение неразрывности; уравнение количества движения; уравнение сохранения энергии.
Уравнение состояния
Для идеального газа уравнение состояния имеет вид

где Л — газовая постоянная.
Для перегретого пара это уравнение неточно, так как коэффициент К зависит от давления и температуры. Значительно точнее соблюдается зависимость

которая говорит о том, что линии постоянной энтальпии отвечает постоянное произведение рх>.
Недостаточная точность, которая получается, если пользоваться приведенными формулами, а также то обстоятельство, что при расширении пара процесс часто переходит из области перегретого в область влажного пара, когда расчет по этим формулам еще менее надежен, заставляют пользоваться таблицами водяного пара.
Широкое распространение при расчетах получили также различные диаграммы водяного пара, в особенности Л,диаграмма. Вместе с тем следует помнить, что точность расчетов с помощью А, ^-диаграммы зависит от масштаба, в котором она построена, и от пределов изменения состояния.

В настоящее время взаимозависимости термодинамических свойств водяного пара представлены формулами, обеспечивающими точность согласно таблицам водяного пара. Однако для учебных целей, для многих инженерных расчетов перовых турбин можно пользоваться упрощенными зависимостями, представленными в приложении 1. Примеры применения зависимостей для расчетов паровых турбин, и в частности довольно простая программа для использования этих зависимостей при расчетах на ЭВМ (см. приложение 1), имеются в задачнике по паровым и газовым турбинам.
Если предположить, что расширение пара происходит без потерь и без теплообмена с внешней средой, то этот процесс называется и з о э н т -ропийным и изменение состояния пара подчиняется уравнению изоэнтропы
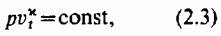
 (рис. 2.1). Показатель изоэнтропы к для перегретого водяного пара изменяется в пределах (рис. 2.1). Показатель изоэнтропы к для перегретого водяного пара изменяется в пределах
х = 1,26-М,33 и в среднем принимается х=1,3; для сухого насыщенного пара х= 1,135.
На рис. 2.1 изоэнтропийный процесс расширения пара в А, ^-диаграмме представлен штриховой линией.
Уравнение неразрывности
Если через канал проходит массовый расход пара Сх и в сечении 1 площадью Рх скорости пара с,, ортогональные к площади Рх, а также значения удельного объема Vx переменны, то уравнение неразрывности запишется в следующем виде:

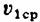 — скорость и удельный объем пара, усредненные по уравнению неразрывности (по расходной составляющей). В общем виде для канала уравнение неразрывности записывается в виде — скорость и удельный объем пара, усредненные по уравнению неразрывности (по расходной составляющей). В общем виде для канала уравнение неразрывности записывается в виде

В дифференциальной форме это уравнение принимает вид
показывая, что приращение площади поперечного сечения канала определяется суммой приращения скорости потока и приращения удельного объема, которое зависит от термодинамического изменения состояния при истечении.
Если записывается уравнение неразрывности для канала, образуемого вращающимися рабочими лопатками, то в зависимости (2.3) — (2.5) вместо скорости с подставляется скорость в относительном движении (относительная скорость) и>, т. е.
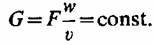
Уравнение количества движения
При направлении движения х и силе сопротивления /?, отнесенной к 1 кг массы пара (подразумевается общий случай движения пара с потерями энергии), дифференциальное уравнение изменения количества движения (уравнение импульсов) в одномерном потоке имеет вид


Здесь левая часть равенства представляет собой приращение кинетической энергии потока, которая равняется разности работы расширения пара при истечении (первый интеграл правой части равенства) и работы сил трения (второй интеграл правой части).
 и закон изменения сил сопротивления К=/(х). Особенно просто эта задача решается в случае изоэнтропийного течения, т. е. течения без потерь и без теплообмена с внешней средой: при этом /? = 0, а уравнение изменения состояния выражается изоэнтропой (2.3) и закон изменения сил сопротивления К=/(х). Особенно просто эта задача решается в случае изоэнтропийного течения, т. е. течения без потерь и без теплообмена с внешней средой: при этом /? = 0, а уравнение изменения состояния выражается изоэнтропой (2.3)
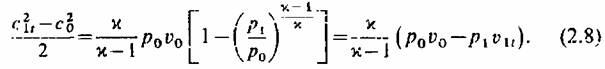
Уравнение сохранения энергии
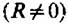 или происходит без потерь (Р-=0): или происходит без потерь (Р-=0):
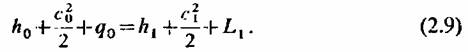
Здесь д0 — количество теплоты, подведенной к I кг пара; Ьх—работа, развиваемая 1 кг пара.
В дифференциальной форме уравнение (2.9) имеет вид

Полученные выше уравнения позвоняют решать ряд практических задач расчета каналов. Воспользуемся уравнением (2.9) и допустим, что пар протекает через канал, в котором отсутствует обмен энергией с внешней средой. Тогда найдем приращение кинетической энергии при расшиоении пара:

Таким образом, изменение кинетической энергии потока пара определяется изменением энтальпии.
Учитывая равенство (2.2), формулу (2.10) можно написать как

где для реального потока в отличие от формул (2.8), выведенных в предположении изоэнтропийного течения, с1
 , необходимо иметь лишь значения энтальпий в начале и конце процесса. , необходимо иметь лишь значения энтальпий в начале и конце процесса.
Таким образом, при отсутствии теплообмена с внешней средой (при адиабатическом течении) приращение кинетической энергии определяется лишь начальным и конечным состояниями пара и не зависит от закона изменения потерь (в процессе расширения).
Если энтальпия пара уменьшается в результате расширения, то кинетическая энергия струи возрастает, скорость г, при выходе из канала становится больше, чем скорость г0 при входе в канал. Такое течение называется конфузорным.
Если при расширении пара энтальпия его не меняется, т.е. А1=Л0, что, например, имеет место при дросселировании пара, то скорость парового потока остается неизменной: с,=г0. Наконец, возможен случай, когда энтальпия пара при выходе из капала больше, чем при входе. Рост энтальпии возможен (при отсутствии теплообмена с внешней средой), если скорость в конце процесса оказывается меньше, чем в начале. Такое течение называется диффузорным.
Рассмотрим различные случаи применения записанных выше уравнений для расчета канала.
Решая уравнение (2.10) относительно сх, находим
 а с скорость, м/с. а с скорость, м/с.
Энтальпия Л0 подводимого пара находится непосредственно из Л, л*-диаграммы (рис. 2.1). Если энтальпия п1 в конце процесса расширения также задана, что формула (2.12) позволяет найти скорость пара. Допустим, что течение происходит без потерь и теплообмена с внешней средой, тогда процесс расширения пара в канале протекает по изоэнтропе. Зная давление ру пара при выходе из капала и проведя в Л, ^-диаграмме (рис. 2.1) изоэитропу А -В, найдем А,,, а следовательно, и скорость си.
Канал, в котором поток плавно ускоряется, называется сопловым или просто соплом.
Согласно формуле (2.8)

 параметрами изоэнтропийно заторможенного потока, или параметрами торможения. Тогда параметрами изоэнтропийно заторможенного потока, или параметрами торможения. Тогда

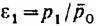 —отношение давления рх к давлению затор- —отношение давления рх к давлению затор-

Давления р0 и рх в отличие от давлений заторможенного потока (полных давлений) называются статическими.
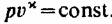
Наконец, если скорость с0 невелика и не превышает 100— 150 м/с, то для определения параметров торможения удобно пользоваться следующими приближенными формулами:

Учитывая, что распространение звука происходит со скоростью
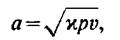
можно, преобразовав формулу (2.11) с учетом (2.13), привести ее к виду
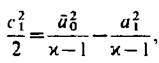 (2.15) (2.15)
 ; ;
 — скорость звука при параметрах торможения. — скорость звука при параметрах торможения.
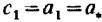 , то такую скорость и соответст- , то такую скорость и соответст-
вующие ей параметры называют критическими и обозначают звездочкой.
Критическое отношение давлений при си = аи — а^ равно
 I а критическая скорость потока I а критическая скорость потока
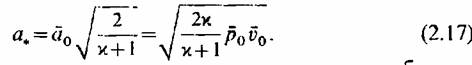 течения широко используются оезразмерные скорости: Як — Сх1ск и число Маха М1=с1/а1. При критическом отношении давлений 8 они равны единице: течения широко используются оезразмерные скорости: Як — Сх1ск и число Маха М1=с1/а1. При критическом отношении давлений 8 они равны единице:

 _ _ ,, подсчитываемый от параметров торможения. Построены кривые _ _ ,, подсчитываемый от параметров торможения. Построены кривые

изменения давления />, удельного объема г„ скорости пара сх и площади Г поперечного сечения сопла.
Последняя кривая_ показывает, что при определенной величине теплоперепада Нч площадь сечения сопла имеет минимум Рт и что дальнейшее расширение пара требует постепенного увеличения площади сечения К При изоэнтропийном течении минимальное сечение сопла, а также параметры пара, которые соответствуют этому сечению, совпадают с критическим, т. е. скорость потока с, в минимальном сечении сопла достигает скорости распространения звука а и с{~а — ат. Используя уравнение неразрывности, находим
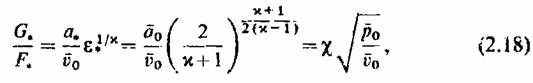
где (7*— критический расход пара, кг/с; Рш~ -площадь канала в критическом сечении, м2; р0 - давление торможения, Па; й0— удельный объем пара при давлении торможения, м*/кг;
 — коэффициент, зависящий от показателя — коэффициент, зависящий от показателя
изоэнтропы х.
Формулы и соответствующие коэффициенты для критических параметров и изоэнтропийного процесса при различных значениях показателя изоэнтропы к представлены в табл. 2.1 (где р, Па).

Приведенный (относительный) расход, выраженный в долях критического, равен

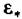 и сверхзвуковая область в пределах изменения 8 от с* до 0. и сверхзвуковая область в пределах изменения 8 от с* до 0.
 равна равна

 уменьшается по уменьшается по
мере расширения пара. В сверхзвуковой области дальнейшее ускорение потока требует постепенного расширения сечения канала (см. также рис. 2.2). Как указывалось, минимальное сечение канала при изоэнтропийном течении отвечает критическому состоянию, которое достигается тогда, когда скорость потока становится равной скорости распространения звука.
 Для того чтобы наглядно показать причину, вызывающую сокращение площади поперечного сечения Р в докритической зоне и рост ее в сверхкритической области, используем уравнение неразрывности в дифференциальной форме (2.5): Для того чтобы наглядно показать причину, вызывающую сокращение площади поперечного сечения Р в докритической зоне и рост ее в сверхкритической области, используем уравнение неразрывности в дифференциальной форме (2.5):

Это выражение показывает, что приращение площади сечения ханала имеет отрицательное или
положительное значение в зависимости от того, какое из, слагаемых правой части равенства больше по абсолютной величине. Нетрудно убедиться, что если в докритической области величина йсс превышает Л/г, что приводит к отрицательному <#7/% т. е. к уменьшению площади проходного сечения, то при переходе в сверхкритическую область приращение объема пара в процессе расширения начинает преобладать над приращением скорости потока и проходное сечения канала увеличивается.
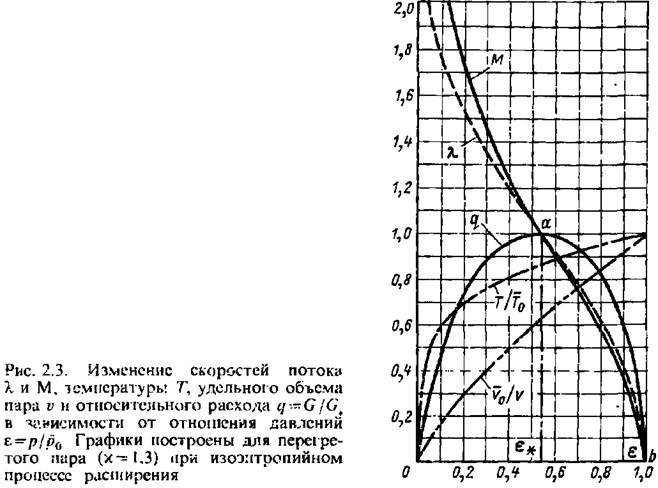
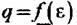 изображена на рис. 2.3. изображена на рис. 2.3.

 . При режимах, когда сх достигает скорости звука, т. е. становится равной критической скорости ап (а также при состояние пара в любом сечении суживающегося сопла перестает зависеть от состояния пара за соплом. . При режимах, когда сх достигает скорости звука, т. е. становится равной критической скорости ап (а также при состояние пара в любом сечении суживающегося сопла перестает зависеть от состояния пара за соплом.
 , отношения удельных объемов V^V^, абсолютных , отношения удельных объемов V^V^, абсолютных
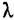 , числа М и приведенного расхода <? дляизоэнтропийного процесса. Для ряда значений показателя изоэнтропы х эти таблицы приведены в численном виде [12]. , числа М и приведенного расхода <? дляизоэнтропийного процесса. Для ряда значений показателя изоэнтропы х эти таблицы приведены в численном виде [12].
 на рис. 2.3 с достаточным на рис. 2.3 с достаточным
приближением является дугой эллипса. Тогда

Для некоторых практических расчетов формула (2.21) дает вполне удовлетворительную точность.
|