Паровые турбины. Часть 1Реальное течение пара в каналах
При расчете реального процесса в отличие от изоэнт-ропийного использование рассмотренных в предыдущем параграфе уравнений (2.4), (2.7), (2,9), (2.11), (2.15) требует учета сил сопротивления, или коэффициентов трения, или коэффициентов потерь. Расчет каналов и характеристик потока без учета потерь может привести к результатам, существенно отличающимся от действительных. Это в свою очередь снизит эффективность турбины.
При обтекании паром стенки канала, и в частности при обтекании турбинной лопатки, влияние вязкости и вызванных ею сил трения обычно ограничивается небольшой зоной непосредственно около стенки. Скорость потока в этой зоне должна меняться от с = 0 на стенке, где поток как бы прилипает к стенке и полностью заторможен, до скорости с в так называемом ядре потока, где влияние сил трения практически уже не сказывается.
Узкая, прилегающая к стенке часть потока, где в данном сечении скорость течения возрастает от нуля до своего полного значения во внешнем • потоке, называется пограничным слоем.
Теория пограничного слоя и результаты исследования подробно рассматриваются в специальных трудах, в общих и прикладных курсах гидроаэромеханики (см., например, [12, 14, 43]). Здесь кратко представлены только общие понятия и некоторые формулы, относящиеся к простым частным случаям.
В зависимости от режима течения различают ламинарный и турбулентный пограничные слои. Последний отличается интенсивным перемешиванием, образованием мелких вихрей, пульсаций скорости, наличием значительной поперечной скорости, тепло- и массообменом с внешним потоком.
В связи с плавным характером перехода пограничного слоя в ядро потока принято условно считать, что пограничный слой заканчивается при толщине 5, где скорость отличается от скорости внешнего потока на 1% (рис. 2.4).

По мере обтекания стенки с мало меняющейся скоростью внешнего потока толщина пограничного слоя 8 увеличивается. Если вначале слой ламинарный (участок /), то при определенных условиях из-за образования и интенсификации пульсаций слой начинает турбулизироваться. Участок //, где происходит этот процесс, называется переходным, а на участке слой можно считать турбулентным. Однако и здесь между стенкой и турбулентным слоем находится тонкий ламинарный подслой.
Толщина турбулентного слоя заметно больше, чем предшествующего ему ламинарного слоя. Турбулентный слой имеет более полную эпюру скоростей, чем ламинарный (см. эпюры скоростей на рис. 2.4), что объясняется интенсивным перемешиванием внутри слоя.
Основным критерием, определяющим влияние вязкости и, в частности, режим пограничного слоя и его толщину, является безразмерное число Рейнольдса

где с—скорость потока; х — характерный размер; V — кинематическая вязкость.
Для анализа обтекания лопаток важно установить возможность отрыва пограничного слоя от обтекаемой поверхности. Рассмотрим обтекание криволинейной поверхности с различным характером основного потока — конфузорным (ускоряющимся) и диффузорным (замедляющимся).
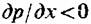 и поток конфу-зорный. В таком потоке толщина пограничного слоя 5 увеличивается незначительно, а при больших ускорениях потока может даже уменьшиться, т. е. возможно утонение пограничного слоя. и поток конфу-зорный. В таком потоке толщина пограничного слоя 5 увеличивается незначительно, а при больших ускорениях потока может даже уменьшиться, т. е. возможно утонение пограничного слоя.
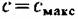 (точка А на рис. 2.5). Начиная с точки А течение (точка А на рис. 2.5). Начиная с точки А течение
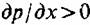 . Скорость с вблизи . Скорость с вблизи
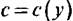 становится около стенки не выпуклой, становится около стенки не выпуклой,

В точке Б кинетическая энергия частиц в пограничном слое оказывается недостаточной для преодоления повышения давления. Скорость <=0 в некоторой прилегающей к самой стенке части слоя, а не только у самой стенки.
Дальнейшее повышение давления из-за тормозящего воздействия перепада давления, направленного против потока. приводит к возникновению возвратного движения (см. эпюру скоростей в пограничном слое в сечении В. рис. 2.5). При

этом пограничный слой из-за оттеснения от стенки существенно утолщается, происходит его отрыв и потери при обтекании стенки резко возрастают.
Эти рассуждения, подтвержденные экспериментально, показывают, что отрыв пограничного слоя при обтекании плавной поверхности с дозвуковыми скоростями может происходить только в диффузорном (замедляющемся) потоке.
Важно отметить, что более полная эпюра скоростей в турбулентном слое, большая кинетическая энергия частиц, движущихся вблизи стенки, приводят к тому, что турбулентный слой отрывается по сравнению с ламинарным ниже по потоку.
Если обтекаемая поверхность гидравлически шероховата, когда бугорки неровной поверхности выходят за ламинарный подслой, и поток у стенки, срываясь с этих бугорков, интенсивно завихривается, то потери при обтекании стенки будут зависеть только от величины этой шероховатости.
 —средняя величина элементов шероховатости. —средняя величина элементов шероховатости.
 зависит от обработки лопаток и изменения их поверхности при эксплуатации вследствие эрозии, коррозии, отложения солей и оксидов. Средние значения Аш, мм, представлены ниже. зависит от обработки лопаток и изменения их поверхности при эксплуатации вследствие эрозии, коррозии, отложения солей и оксидов. Средние значения Аш, мм, представлены ниже.

Кинематическая вязкость V водяного пара (находится по термодинамическим таблицам [39] или рис. П.З в приложении) увеличивается с уменьшением давления и температуры и на входе в паровую турбину в несколько сотен раз меньше, чем на выходе из нее.
Для расчета обтекания турбинных лопаток и анализа проводимых экспериментальных исследований используются так называемые условные толщины пограничного слоя: толщина вытеснения, используемая в уравнении неразрывности; толщина потери импульса — в уравнении количества движения; толщина потери энергии. Эти и другие характеристики пограничного слоя зависят от его режима (ламинарного или турбулентного), числа Рейнольдса, относительной шероховатости [12, 43, 44].
Теория и основные зависимости пограничного слоя являются удобным аппаратом для расчета реального потока. При решении практических задач для большей части потока вне пограничного слоя можно использовать уравнения движения без учета сил трения, базирующиеся на уравнении изоэнтропы (2.3), а для узкой зоны пограничного слоя используются полуэмпирические зависимости, учитывающие влияние сил трения.
В настоящее время имеются решения уравнения Навье-Стокса, учитывающие вязкость.
Записав уравнение энергии (2.10) как для общего случая реального потока при отсутствии обмена энергии с внешней средой
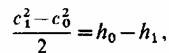
так и для частного случая изоэнтропийного процесса

можно найти разность кинетических энергий теоретического и реального потоков:
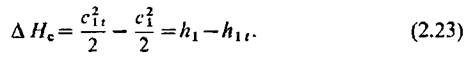
Здесь и далее индекс с показывает, что речь идет о соплах или сопловых решетках.
Относительная величина этой потери называется коэффициентом потерь и находится как
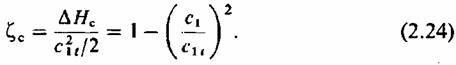
В результате потерь процесс расширения отклоняется от изоэитропы в сторону возрастания энтропии, как показано на рис. 2.1. Это отклонение тем больше, чем больше потери, возникающие в потоке. В предельном случае можно представить себе такое течение, при котором кинетическая энергия полностью переходит в теплоту. В этом случае разность энтальпий в начале и конце расширения обращается в нуль:
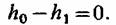
Такой процесс называется дросселированием.
|