Практическая вибродиагностика и монтиторингСвойства вибросигнала роторных агрегатов.
Представление вибросигнала полигармонической и квазиполигармонической моделями.

В роторных агрегатах одной из основных частот возбуждения вибрации является оборотная (роторная) частота, называемая в дальнейшем частотой вращения ротора:

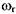 - угловая частота вращения ротора. - угловая частота вращения ротора.
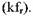
Таким образом, информативными параметрами в такой модели колебаний являются значения амплитуд дискретных составляющих спектра на частоте вращения ротора и ее гармониках и скорость их изменения при увеличении наработки механизма. Амплитуды колебаний на роторных частотах определяются чаще всего величиной дисбаланса, несоосностью валов, кинематическими погрешностями и отношением критической частоты вращения ротора к рабочей.
Помимо упомянутой выше вибрации, кратной частоте вращения ротора, в спектре вибросигнала роторного агрегата могут присутствовать такие характерные частотные составляющие, как

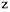 равно числу зубьев шестерни; для турбины, насоса и вентилятора — числу лопаток рабочего колеса и т. п. равно числу зубьев шестерни; для турбины, насоса и вентилятора — числу лопаток рабочего колеса и т. п.
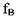 диагностируемого узла агрегата. Первичный процесс локализации источников повышенной виброактивности конструкции агрегата состоит как раз в выявлении потенциальных источников возбуждения, вызывающих колебания на данной частоте. диагностируемого узла агрегата. Первичный процесс локализации источников повышенной виброактивности конструкции агрегата состоит как раз в выявлении потенциальных источников возбуждения, вызывающих колебания на данной частоте.
Практика вибродиагностики роторных агрегатов показала, что полигармоническая модель вибросигнала является лишь нулевым приближением в описании сложного колебательного процесса реального агрегата, хотя может с успехом использоваться в задачах локализации источников и в задачах диагностирования грубых дефектов типа разрушения лопаток турбины, деталей подшипников, поломки зубьев и т. п., вызывающих существенное увеличение уровня колебаний на определенных частотах. В работе реального агрегата абсолютное повторение с течением времени условий взаимодействия его деталей между собой и с внешней средой практически невозможно.
Погрешности изготовления и монтажа деталей, температурные изменения геометрических параметров деталей и зазоров в сочленениях, изменение вязкости смазки, искажение формы и качества поверхностей взаимодействующих деталей с наработкой, наконец, нестабильность оборотов вала двигателя, вызванная, например, нестабильностью частоты сетевого напряжения, и множество других случайных факторов приводят к флуктуациям амплитуд и размытию дискретных линий спектра полигармонических колебаний.
Более адекватной моделью процесса возбуждения колебаний является суперпозиция узкополосных случайных процессов с кратными средними частотами:
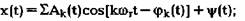
 — уровень шумового возбуждения. — уровень шумового возбуждения.

Энергетический спектр такого процесса (см. рис. 1 — 03) сосредоточен в узких полосах частот в окрестности кГг.
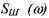
рассматриваемом диапазоне частот. Такая форма представления вибросигнала достаточно хорошо моделирует износ контактирующих поверхностей зубьев колес в редукторе, в подшипниках качения и т. п.
Соотношение энергии периодического и шумового компонентов является информативным параметром вибросигнала, широко используемым при формировании диагностических признаков состояния агрегата.
Импульсная модель акустического сигнала.
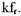 Э ту информацию может дать модель, Э ту информацию может дать модель,
базирующаяся на представлении процессов возбуждения колебаний в роторных агрегатах в виде периодической последовательности импульсов определенной формы. Такая модель достаточно универсальна, так как она позволяет математически описать процессы возбуждения колебаний как в роторных механизмах типа зубчатого зацепления, подшипников качения и скольжения, турбинах, вентиляторах, циркуляционных и центробежных насосах, так и в поршневых машинах с механизмами циклического ударного действия.
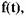 можно представить периодическую последовательность импульсов в виде можно представить периодическую последовательность импульсов в виде
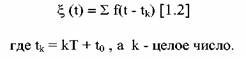
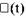 может быть как детерминированной, так и случайной, отражающей может быть как детерминированной, так и случайной, отражающей
случайность одиночного импульса, которая заключается в том, что его амплитуда, длительность и момент появления могут быть, вообще говоря, случайными величинами.
В ряде практических моделей вибросигнала функционирующих механизмов имеет место периодическая последовательность импульсов, модулированных по амплитуде, при неизменной форме, длительности и частоты следования импульсов. Такой вид модуляции, называемой амплитудно-импульсной модуляцией (АИМ), наиболее часто используется для математического представления акустического сигнала.
 , то имеет место временная импульсная модуляция (ВИМ). При этом различают фазово-импульсную модуляцию (ФИМ), когда импульсы имеют постоянную амплитуду и длительность, а меняется их положение на оси времени от периода к периоду, частотно-импульсную модуляцию (ЧИМ), когда импульсы сохраняют амплитуду и положение на оси времени, но меняется их длительность. Все виды модуляции в той или иной мере применимы к задачам моделирования акустического сигнала. , то имеет место временная импульсная модуляция (ВИМ). При этом различают фазово-импульсную модуляцию (ФИМ), когда импульсы имеют постоянную амплитуду и длительность, а меняется их положение на оси времени от периода к периоду, частотно-импульсную модуляцию (ЧИМ), когда импульсы сохраняют амплитуду и положение на оси времени, но меняется их длительность. Все виды модуляции в той или иной мере применимы к задачам моделирования акустического сигнала.
В работающем агрегате в зависимости от характера физического процесса, протекающего в нем, возможны различные отклонения в последовательности импульсов, которые можно охарактеризовать модуляцией амплитуды, длительности или моментов появления имульсов, однако при функционировании оборудования с заданной функцией взаимодействия деталей, определяющейся кинематикой агрегата, наиболее часто встречается амплитудная модуляция, обусловленная разбросом величины силы взаимодействия его элементов в каких-то пределах (неоднородность структуры контактирующих поверхностей зубьев , приводящая к вариации пятна контакта колес зубчатого зацепления; неравномерность воздушного потока в зазоре, отклонение геометрических размеров лопаток турбины вследствие обгара, эрозии и др.). В то же время погрешность окружного шага или явление заедания в зубчатом зацеплении, изгибная деформация, приводящая к неравномерному размещению лопаток в диске или на рабочем колесе турбины, являются причиной возбуждения модулированных по фазе импульсных колебаний.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
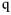 — целое число. Амплитуды комбинационных составляющих равны — целое число. Амплитуды комбинационных составляющих равны
 - суммарная дисперсия модулирующей - суммарная дисперсия модулирующей
функции.
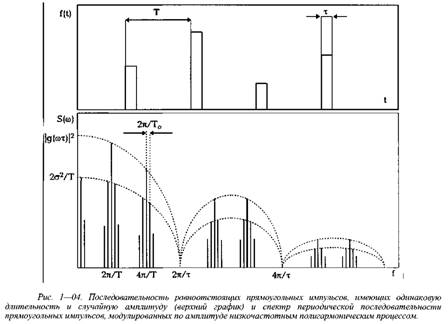
Для формирования диагностического признака используют обычно представление сигнала в достаточно узком диапазоне частот, например в зоне одной из гармоник основной частоты возбуждения механизма (зубцовой, винтовой, лопаточной и др.).
При этом представляют колебания в виде модуляции высокочастотного гармонического сигнала суммой гармонических же низкочастотных колебаний.
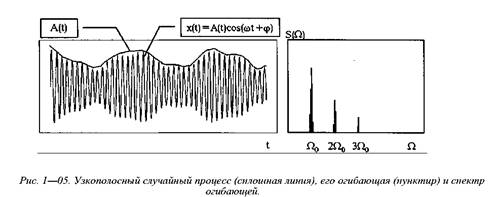
На рис. 1—05 приведен узкополосный случайный процесс (амплитудная модуляция), описываемый математическим выражением вида:
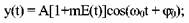
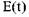 — в общем виде сумма гармонических — в общем виде сумма гармонических
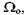 например, частоте например, частоте
вращения шестерни:

Выделение огибающей производится с помощью амплитудного детектора.
|