Теория систем автоматического управленияДискретные алгоритмы управления и дискретная коррекция
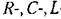 -цепей и т. п. В цифровых системах как алгоритмы управления, так и корректирующие средства реализуются программным путем в виде вычислительной процедуры, организованной в соответствии с разностным уравнением (15.7). -цепей и т. п. В цифровых системах как алгоритмы управления, так и корректирующие средства реализуются программным путем в виде вычислительной процедуры, организованной в соответствии с разностным уравнением (15.7).
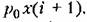
Применительно к передаточной функции ЦВМ (15.8) условие физической реализуемости выполняется, если степень полипома ее числителя не превышает степени полинома знаменателя.
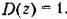 При этом цифровая система формально превращается в импульсную, так как их структурные схемы, изображенные на рис. 15.3 и рис. 14.7, будут одинаковыми. Однако фактически эти системы останутся принципиально различными. При этом цифровая система формально превращается в импульсную, так как их структурные схемы, изображенные на рис. 15.3 и рис. 14.7, будут одинаковыми. Однако фактически эти системы останутся принципиально различными.
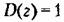 сохраняется весь комплекс сложных устройств (ЦВМ, сохраняется весь комплекс сложных устройств (ЦВМ,
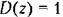 не является рациональным. не является рациональным.
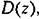 соответствующие рассмотренным в линейным непрерывным алгоритмам. В качестве аналога производной использована не первая разность соответствующие рассмотренным в линейным непрерывным алгоритмам. В качестве аналога производной использована не первая разность
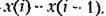 Для вычисления интеграла применены известные приближенные методы интегрирования. Для вычисления интеграла применены известные приближенные методы интегрирования.
При осуществлении дискретной коррекции желаемая передаточная функция 0(2) может быть определена следующим образом. Пусть известна передаточная функция исходной не скорректированной системы

а в процессе решения задачи синтеза определена желаемая передаточная функция разомкнутой системы
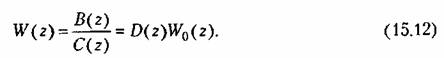
Тогда искомая передаточная функция дискретного корректирующего устройства (передаточная функция ЦВМ)
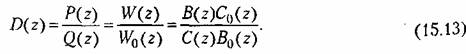
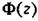 , то вместо (15.13) получим: , то вместо (15.13) получим:
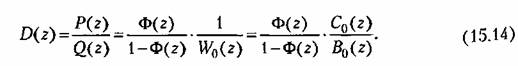
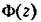 должно производиться с учетом некоторых ограничений. Во-первых, получающаяся передаточная функция ЦВМ (15.13) или (15.14) должна быть физически реализуемой, т. с. степень полинома ее числителя не должна превышать степени полинома знаменателя. Во-вторых должно производиться с учетом некоторых ограничений. Во-первых, получающаяся передаточная функция ЦВМ (15.13) или (15.14) должна быть физически реализуемой, т. с. степень полинома ее числителя не должна превышать степени полинома знаменателя. Во-вторых
 скорректированная система должна быть грубой, т. е. малое изменение ее параметров не должно приводить к существенному изменению характера протекающих в ней процессов. скорректированная система должна быть грубой, т. е. малое изменение ее параметров не должно приводить к существенному изменению характера протекающих в ней процессов.
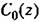 . Невыполнение условий грубости вызывает неустойчивость системы. . Невыполнение условий грубости вызывает неустойчивость системы.
Поясним сказанное примером. Рассмотрим систему (рис. 15.3), передаточная функция непрерывной части которой равна
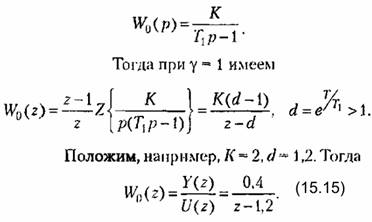 ) )
Введем в систему дискретное корректирующее устройство с передаточной функцией

В результате получим передаточную функцию разомкнутой системы (15.12)
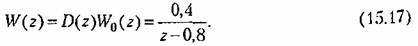
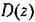 . Таким образом, условие грубости нарушено. . Таким образом, условие грубости нарушено.
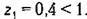
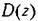 остались прежними. Тогда передаточная функция разомкнутой системы остались прежними. Тогда передаточная функция разомкнутой системы
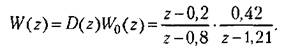
Характеристическое уравнение замкнутой системы имеет вид
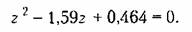
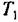 ) привело к существенному изменению поведения системы. ) привело к существенному изменению поведения системы.
Следует отметить, что даже при идеальной компенсации (что, конечно, практически невозможно) сделанный ранее вывод об устойчивости замкнутой системы с передаточной функцией в разомкнутом состоянии (15.17) оказывается неверным. Это связано с тем, что передаточные функции получаются при нулевых начальных условиях, а последствия нарушения условии грубости проявляются при ненулевых начальных условиях. Чтобы убедиться в этом, составим разностные уравнения (см. § 14.3), соответствующие передаточным функциям (15.15) и (15.16):
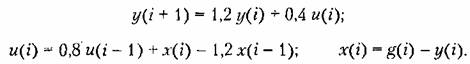
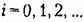 последовательно последовательно
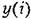
неограниченно увеличивается, т. е. замкнутая система неустойчива.
Вместо формул (15.13) и (15.14) может применяться соотношение, связывающее частотные передаточные функции

или соответствующие им логарифмические частотные характеристики

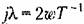 получить передаточную получить передаточную
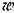 к z-преобразованию — к z-преобразованию —
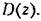
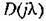 имела степень числителя не больше, чем степень знаменателя. имела степень числителя не больше, чем степень знаменателя.
Поясним сказанное примером. Пусть в цифровой системе с экстраполятором пулевого порядка передаточная функция непрерывной части
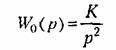
соответствует интегрирующему звену второго порядка. Тогда без коррекции имеем
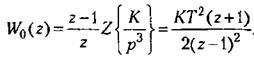
Далее можно получить частотную передаточную функцию
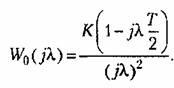
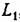 , то желаемая частотная передаточная функция , то желаемая частотная передаточная функция
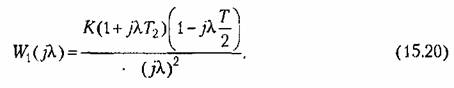
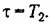 Дискретная частотная передаточная функция требуемого корректирующего звена последовательного типа Дискретная частотная передаточная функция требуемого корректирующего звена последовательного типа
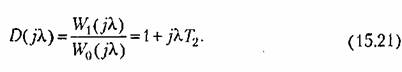
Переход к передаточной функции ЦВМ дает
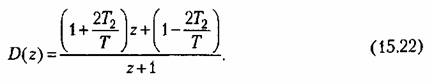
 соответствует границе устойчивости третьего тина и нарушаются условия грубости. соответствует границе устойчивости третьего тина и нарушаются условия грубости.
Заметим, что получившаяся частотная передаточная функция корректирующего устройства (15.21) не может быть реализована, вообще говоря, и в непрерывном варианте. Эта функция соответствует бесконечному подъему усиления при росте частоты до бесконечности. При реализации в дискретном варианте эта функция приводит к не
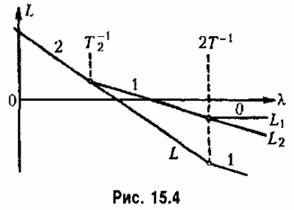
устойчивой программе ЦВМ.
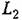 в другом виде (рис. 15.4). Желаемая передаточная функция в другом виде (рис. 15.4). Желаемая передаточная функция
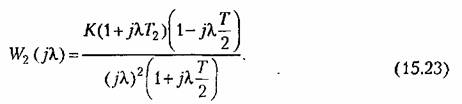
Передаточная функция корректирующего устройства в этом случае имеет вид
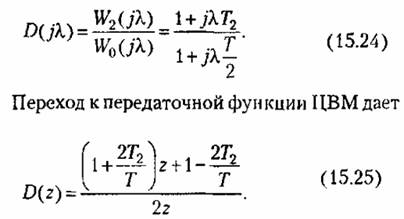
Этой передаточной функции соответствует устойчивая программа ЦВМ, так как условия грубости не нарушаются.
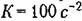 , а показатель колебательности М = 1,5. Дальнейший расчет произведем в соответствии с формулами § 12.6. Базовая частота л. а. х. , а показатель колебательности М = 1,5. Дальнейший расчет произведем в соответствии с формулами § 12.6. Базовая частота л. а. х.
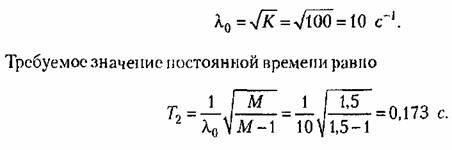
Допустимое значение суммы малых постоянных времени для передаточной функции (15.23) равно периоду дискретности:
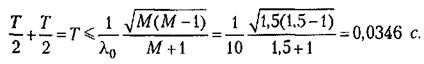
Примем период дискретности Т= 0,0346 с. Передаточная функция ЦВМ (15.25) имеет вид
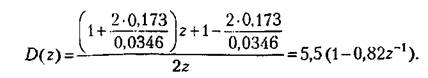
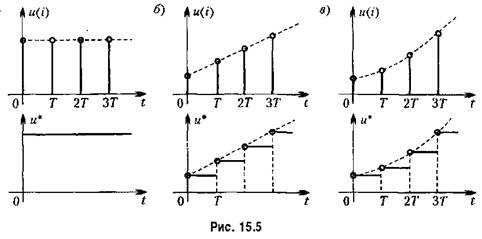
С целью повышения точности ЦВМ может быть использована для повышения порядка астатизма системы или реализации комбинированного управления.
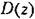 для их дискретных апалогов приведены в табл. 15.1. для их дискретных апалогов приведены в табл. 15.1.
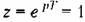 . Поэтому повышение порядка астатизма цифровой системы может быть достигнуто за счет как непрерывных, так и дискретных интеграторов. . Поэтому повышение порядка астатизма цифровой системы может быть достигнуто за счет как непрерывных, так и дискретных интеграторов.
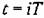 будет иметь пульсации. будет иметь пульсации.
Исследуем вначале возможность появления пульсаций исходя из физических соображений.
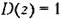 . Тогда в режиме . Тогда в режиме
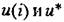 будет изменяться так, как показано па рис. 15.5, а будет изменяться так, как показано па рис. 15.5, а
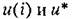 будут такими же по форме, как па рис. 15.5, а, но при пулевой ошибке. будут такими же по форме, как па рис. 15.5, а, но при пулевой ошибке.
 имеет разрывный характер, что приводит к появлению пульсаций. Таким образом, система может воспроизводить линейно изменяющееся задающее воздействие без пульсаций (но с ошибкой) только при наличии в ней непрерывного интегратора. Для устранения скоростной ошибки можно использовать дополнительно как непрерывные, так и дискретные интеграторы. имеет разрывный характер, что приводит к появлению пульсаций. Таким образом, система может воспроизводить линейно изменяющееся задающее воздействие без пульсаций (но с ошибкой) только при наличии в ней непрерывного интегратора. Для устранения скоростной ошибки можно использовать дополнительно как непрерывные, так и дискретные интеграторы.
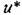 будет изменяться так, как показано на рис. 15.5, б, а при наличии двух дискретных интеграторов — как на рис. 15.5, в. будет изменяться так, как показано на рис. 15.5, б, а при наличии двух дискретных интеграторов — как на рис. 15.5, в.
Для исследования возможности появления пульсаций можно использовать также формулу (14.102). Из нее с учетом выражения (14.67) получим
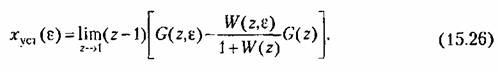
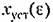 не зависит от е, то пульсации отсутствуют. не зависит от е, то пульсации отсутствуют.
В качестве примера рассмотрим систему, передаточная функция непрерывной части которой
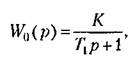
при наличии дискретного аналога интегрирующего звена с передаточной функцией
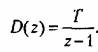
По формулам (14.60) и (14.62) находим:
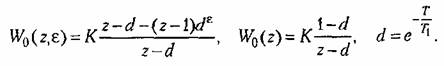
Передаточные функции разомкнутой системы (15.10) и (15.9) имеют вид
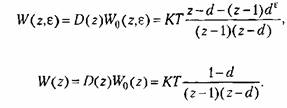
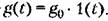 Его изображение Его изображение
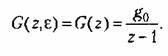
По формуле (15.26) находим установившуюся ошибку системы
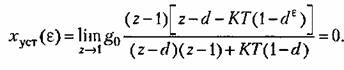
Таким образом, при введении дискретного интегратора статическая ошибка полностью устраняется, что соответствует сделанному ранее выводу.
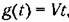 имеем имеем
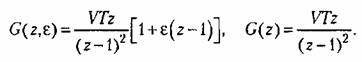
Аналогично предыдущему получаем:
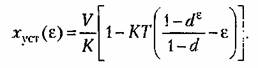
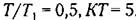
В цифровых системах возможно использование комбинированного управления но задающему или возмущающему воздействиям. При выполнении заданных условий по точности комбинированное управление позволяет снизить требования к основному каналу
Комбинированное управление особенно удобно применять в тех случаях, когда задающее воздействие вычисляется в управляющей ЦВМ. В этом случае на ЦВМ может быть также возложена задача вычисления производных этого воздействия, что
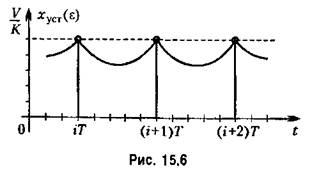
позволяет просто реализовать схемы, аналогичные рассмотренным в § 9.2.Подобное положение возникает, например, при слежении телескопов за планетами, при управлении по счисляемым координатам и т. н. Структурная схема системы комбинированного управления для случая использования дополнительного канала с передаточной функцией Е(г) по задающему воздействию изображена на рис. 15.7.
 Эквивалентная передаточная функция замкнутой системы с учетом дополнительного канала Эквивалентная передаточная функция замкнутой системы с учетом дополнительного канала

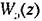 — эквивалентная передаточная функция разомкнутой системы. Эквивалентная передаточная функция по ошибке — эквивалентная передаточная функция разомкнутой системы. Эквивалентная передаточная функция по ошибке
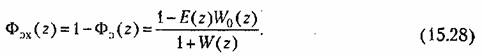
Эквивалентная передаточная функция разомкнутой системы
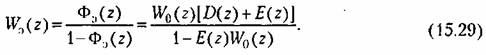
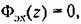 можно получить условие полной можно получить условие полной
инвариантности

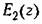 и формула (15.30) может быть приведена к виду и формула (15.30) может быть приведена к виду
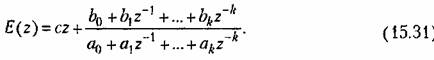 ) )
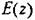 необходимо использовать упрежденное на один такт значение необходимо использовать упрежденное на один такт значение
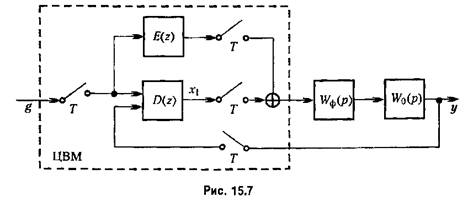
 задающего воздействия. Это связано с необходимостью применения прямых разностей, которые в дискретном плане должны здесь заменить процесс дифференцирования. При этом возможны следующие ситуации. задающего воздействия. Это связано с необходимостью применения прямых разностей, которые в дискретном плане должны здесь заменить процесс дифференцирования. При этом возможны следующие ситуации.
Если ЦВМ вычисляет значение задающего воздействия но некоторым заложенным в нее данным и использует при атом прогнозирование (например, при вычислении текущих координат небесных тел, спутников, ракет и др.), то вычисление будущего значения интересующей величины может быть легко сделано со сдвигом на практически любое число тактов, В этом случае реализация формулы (15.31) в принципе возможна. Однако практические трудности в реализации слишком сложных алгоритмов и ограничения в элементах не дают возможности получить полную инвариантность.
Если ЦВМ вычисляет задающее воздействие не по принципу прогнозирования, а в результате обработки поступающей текущей информации, то точная реализация формулы (15.31) оказывается невозможной. Тогда приходится ограничиться приближенной реализацией формулы (15.30) либо вводить в прямой капал дополнительное запаздывание па один такт. В нервом случае условие полной инвариантности (15.30) нарушается, во втором — вводится постоянное временное запаздывание па один такт в обработку задающего воздействия, что также нарушает условие инвариантности.
Таким образом, при использовании комбинированного управления приходится ориентироваться не на полную инвариантность, а па некоторое, во многих случаях весьма существенное, повышение точности.
Поскольку точность систем управления определяется низкочастотной частью л, а. х., а низкочастотная часть л. а. х. дискретных систем практически сливается ел. а. х. непрерывной части системы, то расчет дискретных систем комбинированного управления осуществляется аналогично непрерывному случаю [9].
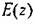
|