Теория систем автоматического управленияМетод последовательных приближений
Рассмотрим уравнение (13.1):
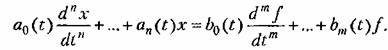
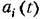 меняются медленно, найдем функцию веса для этого уравнения. меняются медленно, найдем функцию веса для этого уравнения.
Переменные коэффициенты в левой части исходного уравнения представим в виде суммы постоянной и изменяющейся частей:
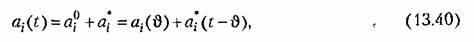

Тогда исходное дифференциальное уравнение (13.1) можно представить в виде
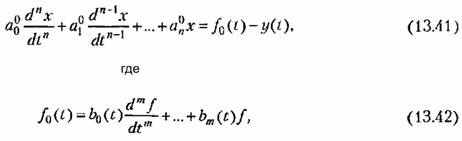

 мала по сравнению с левой частью (13.41). Эту функцию можно рассматривать как возмущение, и тогда к уравнению (13.41) можно применить метод последовательных приближений. мала по сравнению с левой частью (13.41). Эту функцию можно рассматривать как возмущение, и тогда к уравнению (13.41) можно применить метод последовательных приближений.
В уравнении (13.41) можно перейти к изображениям по Лапласу. Тогда получим

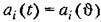 . Тогда первое приближение может быть найдено как решение дифференциального уравнения . Тогда первое приближение может быть найдено как решение дифференциального уравнения
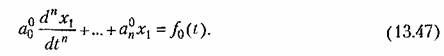
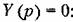

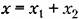 . Тогда получается уравнение с фиксированными коэффициентами для определения поправки: . Тогда получается уравнение с фиксированными коэффициентами для определения поправки:
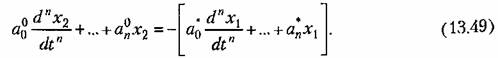
Это уравнение также может быть решено с использованием преобразования Лапласа посредством нахождения оригинала изображения
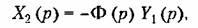
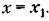
Повторяя этот процесс многократно, можно найти рекуррентное соотношение
для определения к -го члена ряда (13.46):

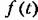
|