Теория систем автоматического управленияТребования к запасу устойчивости
В следящих системах повышение коэффициента передачи разомкнутой системы вызывает приближение к колебательной границе устойчивости. Это проявляется в увеличении колебательности системы. Для оценки запаса устойчивости, т.е. степени удаления от колебательной границы устойчивости, могут использоваться различные критерии, в том числе такие, как, например, перерегулирование при единичном входном возмущении, запас устойчивости но амплитуде и по фазе и т.п.
При использовании частотных критериев качества наиболее удобно оценивать запас устойчивости замкнутой системы по показателю колебательности М, который характеризует склонность системы к колебаниям (см. гл. 8).
В астатических системах для замкнутой системы коэффициент передачи на нулевой частоте равен единице. Поэтому под показателем колебательности понимается абсолютное значение наибольшего максимума
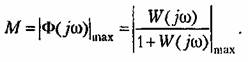
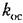 : :

где К - коэффициент передачи разомкнутой системы.
Отсюда находится требуемое значение коэффициента обратной связи:


Необходимым и достаточным условием того, чтобы в устойчивой системе показатель колебательности был не больше заданного, является нахождение фазовой характеристики вне запретной зоны (рис. 8.21). В минимально-фазовых системах это условие может быть выдержано соблюдением определенных правил построения л. а. х. без нахождения фазовой характеристики.
Рассмотрим принципы построения л. а. х. с заданным показателем колебательности. По методическим соображениям рассмотрение начнем со следящих систем с астатизмом второго порядка, хотя эти системы и не относятся к наиболее простым и распространенным.
Как правило, в качестве типовых используются л. а. х„ имеющие в низкочастотной части наклон не более -40 дБ/дек. Это вызвано стремлением избавиться от условий, при которых возможно появление неустойчивости в большом, т. е. при согласовании следящей системы с большого угла.
Типовые л. а, х. систем с астатизмом второго порядка. В системах с астатизмом второго порядка обычно имеются два интегрирующих звена. Такими звеньями могут быть исполнительный и вспомогательный двигатели, например гидромуфта и управляющий двигатель, поворачивающий шпиндель или чашу гидронасоса. В некоторых случаях астатизм второго порядка может появляться вследствие особенностей механических характеристик единственного исполнительного двигателя, у которого вращающий момент не зависит от скорости вращения.
Рассмотрим передаточную функцию разомкнутой системы вида
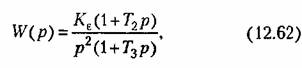
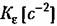 — коэффициент передачи по разомкну- — коэффициент передачи по разомкну-
той системы, называемый добротностью по ускорению.
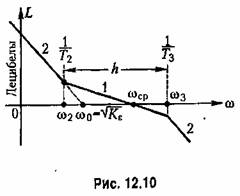
Асимптотическая л. а. х., соответствующая (12.62), изображена на рис. 12.10. В соответствии с наклонами асимптот, кратными -20 дБ/дек, ей
присвоен тип
Положение всей л. а. х. может быть задано точкой пересечения первой асимптоты с осью пуля децибел. Этой точке соответствует частота

которую назовем базовой.
 передаточная функция будет представлена в нормированном виде; передаточная функция будет представлена в нормированном виде;
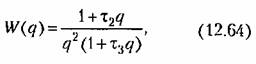
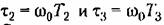 — относительные постоянные времени. — относительные постоянные времени.
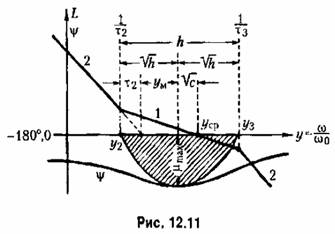
 , изображена на рис. 12.11. Здесь же показаны для иллюстрации фазовая характеристика и запретная область для нее. , изображена на рис. 12.11. Здесь же показаны для иллюстрации фазовая характеристика и запретная область для нее.
Протяженность участка с единичным наклоном, т. е. с отрицательным наклоном 20 дБ/дек, определяется отношением двух постоянных времени (см. § 8.8 и рис. 8.25):

Иод протяженностью участка вдоль оси частот (рис. 12.11) понимается отношение частот конечных точек участка (большей к меньшей). Запас по фазе для функции (12.64)

Максимальный запас по фазе определяется только протяженность асимптоты л. а. х., имеющей единичный наклон.
Приравнивание максимальных запасов по фазе (8.88) и (12.68) дает зависимость между протяженностью участка к и показателем колебательности Мпри оптимальном выборе параметров, т, е. при совпадении максимумов реальной фазовой характеристики и запретной зоны (рис. 12.11):

Эти формулы связывают протяженность участка к с минимальным значением показателя колебательности, который может быть получен при этой протяженности, или величину показателя колебательности М с минимальной протяженностью участка к, обеспечивающей этот показатель колебательности.
Из рис. 12.11 легко найти оптимальнее параметры л. а. х.:
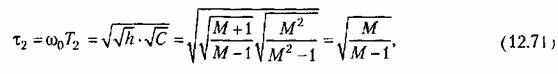
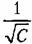 относительной частоте, при которых запас относительной частоте, при которых запас
по фазе (в запретной области) получается максимальным (см. формулу (8.88));

Эти параметры соответствуют минимальному значению показателя колебательности при заданной протяженности участка к.
Следует заметить, что технически реализовать систему тем легче, чем меньше протяженность участка к. Это связано с необходимостью подъема на этом участке верхних частот, что во многих случаях затруднено вследствие наличия в системе внешних и внутренних высокочастотных помех. Поэтому с точки зрения оптимальности инженерного решения необходимо стремиться к реализации желаемых динамических качеств при минимальной требуемой протяженности участка /г.
Для получения заданного показателя колебательности в замкнутой системе при фиксированной базовой частоте л. а. х. необходимо иметь следующие постоянные времени:

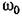 за точку, фиксирующую положение л. а. х. (рис. 12.1 ( и 12.11), можно принять, например, точку пересечения второй асимптоты л. а. х. < за точку, фиксирующую положение л. а. х. (рис. 12.1 ( и 12.11), можно принять, например, точку пересечения второй асимптоты л. а. х. <

 Тогда вместо (12.73) Тогда вместо (12.73)
и (12.74) получим выражения, которые при фиксированной частоте среза, а следовательно, и фиксированном положении запретной зоны для фазовой характеристики можно превратить в неравенства:
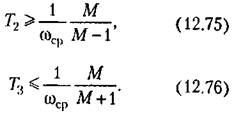
При равенстве левых частей правым показатель колебательности будет равен заданному значению М, При неравенстве левых и правых частей будет вводиться некоторый дополнительный запас устойчивости и показатель колебательности будет снижаться.
Эти формулы легко запоминаются, и они просто связаны с параметрами окружности — запретной зоны па комплексной плоскости (см. рис. 8.22).
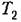 по сравнению с тем, что дает формула, в некоторых случаях может привести к ухудшению запаса устойчивости. по сравнению с тем, что дает формула, в некоторых случаях может привести к ухудшению запаса устойчивости.
При использовании типовой передаточной функции (12.62) может быть предусмотрен дополнительный запас устойчивости для возможности иметь в усилительном канале некоторое количество не учитываемых при расчете малых постоянных времени. Дополнительный запас устойчивости создается уменьшением величины постоянной времени Т-л или, соответственно,
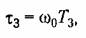
чтобы отодвинуть фазовую характеристику от запретной области (рис. 12.12).
Па малые постоянные времени отводится обычно несколько градусов запаса по фазе. Так, например, в [9] предлагается отводить на эти цели величину, соответствующую сумме малых постоянных,

а число малых постоянных времени принимать равным 4-5-6. Тогда граница малых постоянных времени определяется значением

 которая больше граничной частоты (рис. 12.12) которая больше граничной частоты (рис. 12.12)

го эта постоянная может не учитываться при расчете.
Расчетная формула для определения допустимого значения постоянной времени Т2 (12.73) при этом сохраняется, а вместо формулы (12.74) должно использоваться выражение

В более сложном случае передаточная функция разомкнутой системы может иметь произвольное число постоянных времени, входящих в ее знаменатель:
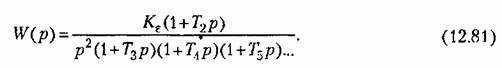
Этой передаточной функции соответствует л. а. х. типа 2-1-2-3-4...
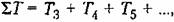 включая малые постоянные времени, должна удовлетворять неравенству включая малые постоянные времени, должна удовлетворять неравенству

 должно выполняться условие (12.75), а для суммы остальных постоянных времени — условие должно выполняться условие (12.75), а для суммы остальных постоянных времени — условие


Возможен случай, когда в передаточную функцию разомкнутой системы входит множитель, соответствующий колебательному звену с комплексными корнями:
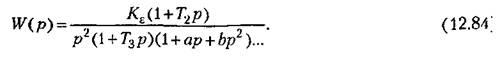
Допустить наличие такого множителя можно в том случае, если частота свободных колебаний звена значительно больше базовой частоты:

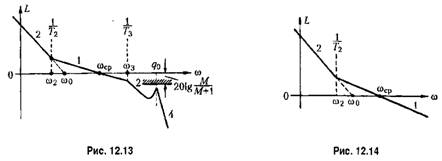
Асимптотическая л. а. х. для этого случая изображена на рис. 12.13.
При выполнении условия (12.85) фазовый сдвиг, вносимый колебательным звеном в районе максимального запаса по фазе, можно принять равным агегд асо. Поэтому коэффициент а должен входить в общую сумму постоянных времени (12.82) или (12.83).
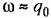 (рис. 12.13), необходимо выполнение дополнительного условия, которое (рис. 12.13), необходимо выполнение дополнительного условия, которое
вытекает из неравенства (8.87):
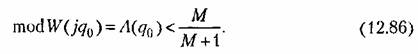
Выполнение этого условия может быть легко проверено при построении л. а. х.
Более подробно этот вопрос рассмотрен для случая гироскопических следящих систем в [9].
 Тогда передаточная функция разомкнутой системы (12.81) приобретает вид Тогда передаточная функция разомкнутой системы (12.81) приобретает вид
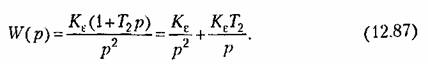
Передаточная функция подобного вида соответствует изодромному управлению. Она может встречаться, например, в сглаживающих системах различного типа, построенных на электромеханических, электронных, гироскопических и тому подобных интеграторах.
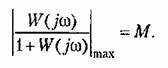
Подстановка (12.87) и исследование пол учившегося выражения на максимум дает следующее условие, которое должно быть выполнено, чтобы показатель колебатель ности не превышал заданного значения:
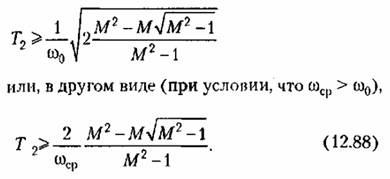
 и не имеет дополнительных корректирующих средств кроме, возможно, жесткой тахометрической обратной связи, передаточная функция разомкнутой системы может быть сведена к виду и не имеет дополнительных корректирующих средств кроме, возможно, жесткой тахометрической обратной связи, передаточная функция разомкнутой системы может быть сведена к виду

Асимптотическая л. а. х. типа 1-2, соответствующая этой передаточной функции, изображена па рис. 12.15.
Определение допустимого значения постоянной времени может быть сделано прямым нахождением максимума амплитудной частотной характеристики замкнутой системы
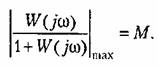
Подставляя (12.89) и исследуя получившееся выражение на максимум, можно найти условие того, чтобы показатель колебательности не превышал заданного значения:

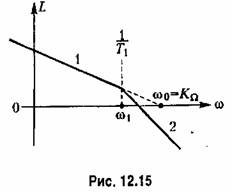
Последняя формула позволяет при заданном значении постоянной времени исполнительного двигателя легко определять максимальное значение добротности по скорости, которое можно иметь в следящей системе при данном значении показателя колебательности.
При заданном значении требуемой добротности по скорости эта же формула позволяет определять допустимое значение постоянной времени исполнительного двигателя и необходимый коэффициент передачи по петле жесткой тахометрической обратной связи, служащей для снижения постоянной времени двигателя. Определение коэффициента передачи для тахометрической обратной связи может производиться по формуле

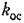 — коэффициент передачи но петле тахометрической обратной связи. — коэффициент передачи но петле тахометрической обратной связи.
В более сложном случае передаточная функция (12.89) может быть представлена в виде
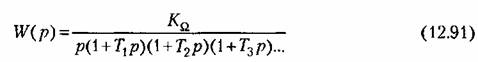
Этой функции соответствует л. а. х. типа 1-2-3-4...
Здесь может быть получена приближенная формула, ориентировочно связыва ющая сумму всех постоянных времени с добротностью по скорости:

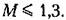
Приближенная формула (12.92) становится точной при М=1и любом числе по стоянных времени либо при наличии только одной постоянной времени и любом зна чении М. В последнем случае она вырождается в формулу (12.90). При значениях М, мало отличающихся от единицы, например при М < 1,3, формула (12.92) является достаточно точной и может использоваться для расчета при наличии любого числа постоянных времени, а также при наличии вре менного запаздывания т, которое должно учи тываться в общей сумме постоянных времени. Л. а. х. рассмотренного типа может исполь зоваться в простейших следящих системах с не высокими требованиями в отношении стати ческой и динамической точности. При невоз можности удовлетворить требованиям технического задания приходится переходить к более сложным тинам л. а. х. На рис. 12.16
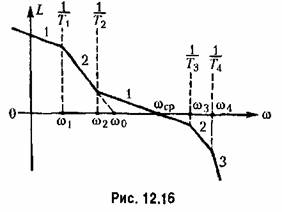
изображена асимптотическая л. а. х. типа 1 -2- 1-2-3... Она может быть получена из соответствующей л. а. х, тина 2-1-2-3... система с астатизмом второго порядка (рис. 12.12)
 . Этой л. а. х. соот- . Этой л. а. х. соот-
ветствует передаточная функция разомкнутой системы

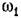 значительно отличается от частоты в зоне максимума требуемого запаса но фазе, то с большой степенью точности расчет можно вести по формулам, полученным для систем с астатизмом второго порядка. В этом случае положение л. а. х., изображенной на рис. 12.16, определяется базовой частотой значительно отличается от частоты в зоне максимума требуемого запаса но фазе, то с большой степенью точности расчет можно вести по формулам, полученным для систем с астатизмом второго порядка. В этом случае положение л. а. х., изображенной на рис. 12.16, определяется базовой частотой
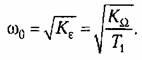
В соответствии с формулами (12.73) и (12.82) имеем
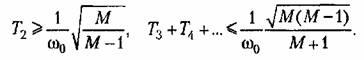
или в соответствии с формулами (12.75) и (12.83)
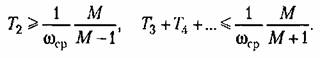
Для уточнения расчета можно учесть то обстоятельство, что по сравнению с системой, имеющей астатизм второго порядка, здесь имеется дополнительный запас но фазе

 (формулы (12.73) и (12.75)). Однако подобное уточнение обычно не имеет практического значения [9] и почти всегда с достаточной степенью точности можно вести расчет параметров л, а. х. тина 1-2-1-2-3... по формулам, которые были получены для системы с астатизмом второго порядка (л. а. х. типа 2-1-2-3...). (формулы (12.73) и (12.75)). Однако подобное уточнение обычно не имеет практического значения [9] и почти всегда с достаточной степенью точности можно вести расчет параметров л, а. х. тина 1-2-1-2-3... по формулам, которые были получены для системы с астатизмом второго порядка (л. а. х. типа 2-1-2-3...).
Типовые л. а. х. статических систем. В простейшем случае передаточная функция разомкнутой статической системы имеет вид

где К— коэффициент передачи разомкнутой системы.
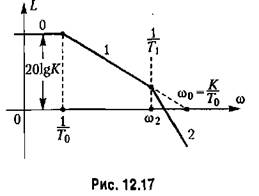
Соответствующая асимптотическая л. а. х. типа 0-1-2 изображена на рис. 12.17.
В районе пересечения л. а. х. оси пуля децибел передаточная функция может быть приближенно сведена к передаточной функции системы с астатизмом первого порядка

Это дает возможность использовать полученную выше формулу (12.90) для л. а. х. типа 1-2 (рис. 12.15) при замене Ка на со0. Тогда можно получить условие обеспечения заданного показателя колебательности

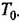
Отклонение передаточной функции (12.96) от более точного выражения (12.95) в области низких частот дает некоторое увеличение запаса устойчивости, т. е. уменьшение колебательности. Учет этого обстоятельства обычно нецелесообразен ввиду незначительности получаемого эффекта [9].
При повышенных требованиях но статической и динамической точности могут применяться л. а. х. типа 0-1-2-1-2-3... (рис. 12.18), образованные из л. а. х. типа 2-1-2-3... (рис. 12.10) систем с астатизмом второго порядка.
Таким л. а. х. соответствует передаточная функция разомкнутой системы
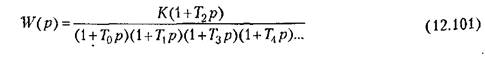
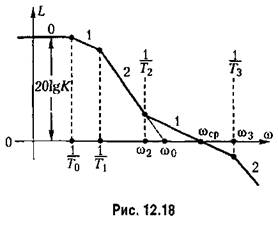
Как и в случае систем с астатизмом первого порядка, здесь можно с достаточной степенью точности пользоваться универсальными формулами (12.73)-(12.76) и (12.82), (12.83).
Учет звеньев постоянного запаздывания и колебательных звеньев, а также введение границы малых постоянных времени может делаться аналогично изложенному выше.
|