Теория систем автоматического управленияКанонические разложения случайных функций
Элементарной случайной функцией называется функция, которая может быть
представлена в виде

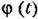 — некоторая известная неслучайная функция времени (синусоида, экспонента, степенная функция и т. н.), х — случайная величина. — некоторая известная неслучайная функция времени (синусоида, экспонента, степенная функция и т. н.), х — случайная величина.
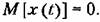 Корреляционная функция в этом случае Корреляционная функция в этом случае
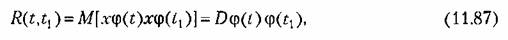
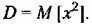
 и элементарных случайных функций: и элементарных случайных функций:

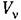 — случайные взаимно некоррелированные коэффициенты с нулевым математическим ожиданием. — случайные взаимно некоррелированные коэффициенты с нулевым математическим ожиданием.
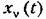 координатных функций. координатных функций.
При использовании канонического разложения значительно упрощается выполнение различных операций над случайными функциями (дифференцирование, интегрирование, решение линейных дифференциальных уравнений и т. п.). Так, например, производная от (11.88) будет
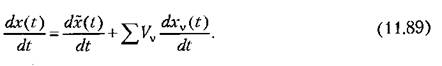
Аналогичным образом интегрирование (11.88) даст
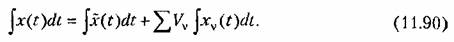
Для нахождения канонического разложения случайных функций существуют различные методы [80].
Из (11.88) может быть найдена корреляционная функция
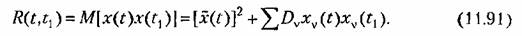
 — дисперсии коэффициентов канонического разложения. — дисперсии коэффициентов канонического разложения.
Таким образом, корреляционная функция может быть выражена через те же координатные функции.
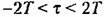 и разложение корреляционной функции может быть задано в виде ряда Фурье: и разложение корреляционной функции может быть задано в виде ряда Фурье:
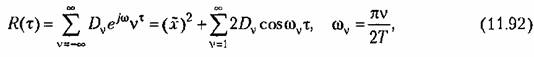
где V — целые числа.
Этому выражению соответствует каноническое разложение самой случайном функции

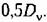 В разложении (11.92) В разложении (11.92)
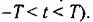
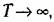 то формулу (11.92) можно представить в виде то формулу (11.92) можно представить в виде
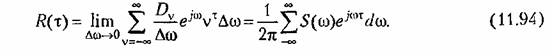
Здесь введена спектральная плотность стационарного процесса (см. § 11.5)
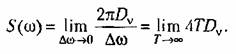
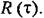
|