Теория систем автоматического управленияПрименение изодромных устройств
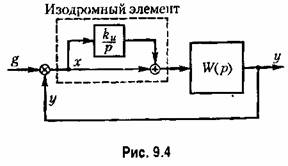
Существует путь повышения порядка ас-татизма системы без заметного или недопустимого ухудшения ее запаса устойчивости. Этот путь заключается в применении изодромных устройств, например таких, как изображенные па рис. 4.19. Структурная схема системы при введении изодром-ного устройства изображена па рис. 9.4. Передаточная функция изодромного устройства может быть представлена в виде

 — постоянная времени изодромного устройства. — постоянная времени изодромного устройства.
 частей, то перемещение чувствительного частей, то перемещение чувствительного

элемента будет пропорциональным отклонению давления от заданного значения:

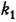 — коэффициент пропорциональности, определяемый жесткостью пружины. — коэффициент пропорциональности, определяемый жесткостью пружины.
 Вместо (5.11) получим Вместо (5.11) получим

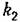 — коэффициент, определяемый скоростным сопротивлением демпфера. — коэффициент, определяемый скоростным сопротивлением демпфера.
Равенство (9.12) соответствует введению интеграла в алгоритм управления.
Наконец, в случае, изображенном на рис. 9.5, в, перемещение чувствительного элемента будет складываться нз деформации пружины и перемещения поршня демпфера:

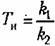 — постоянная времени изодромного устройства. — постоянная времени изодромного устройства.
В качестве второго примера рассмотрим приведенную выше схему следящей системы (рис. 9.2). Переход от введения дополнительного интеграла к введению изодромного устройства может быть сделан добавлением связи, показанной пунктиром. Передаточная функция разомкнутой системы может быть получена умножением (9.1) на передаточную функцию изодромного устройства.
В результате для рассматриваемой схемы получим:

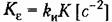 — добротность системы по ускорению. — добротность системы по ускорению.
Коэффициенты ошибки определяются равенствами:

Рассматривая характеристическое уравнение системы

или в ином виде
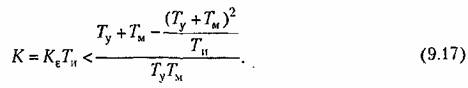
 (это будет при отсутствии интегрирующего (это будет при отсутствии интегрирующего
привода в изодромном механизме) условие устойчивости переходит в неравенство

 дает повышение порядка астатизма на единицу при возможности практически сохранить условия устойчивости в системе, куда этот механизм вводится. дает повышение порядка астатизма на единицу при возможности практически сохранить условия устойчивости в системе, куда этот механизм вводится.
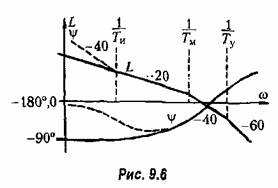
Это обстоятельство можно проиллюстрировать также на логарифмических частотных характеристиках (рис. 9.6). В соответствии с выражением для передаточной функции разомкнутой системы (9.14) можно записать:

 логарифмические характеристики системы с изодромиым устройством логарифмические характеристики системы с изодромиым устройством
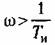
 логарифмические частотные характеристики системы с изодромным устройством практически не отличаются от логарифмических характеристик исходной схемы. В частности, в районе пуля децибел для л. а. х. можно получить одинаковый вид амплитудной и фазовой характеристик для обеих схем, что будет соответствовать одинаковому запасу устойчивости. логарифмические частотные характеристики системы с изодромным устройством практически не отличаются от логарифмических характеристик исходной схемы. В частности, в районе пуля децибел для л. а. х. можно получить одинаковый вид амплитудной и фазовой характеристик для обеих схем, что будет соответствовать одинаковому запасу устойчивости.
На рис. 9.6 сплошными линиями показаны л. а. х. и л. ф. х. для исходной схемы, а пунктирными — изменения, даваемые введением изодромного устройства с относительно большой постоянной времени.
Следует заметить, что введение изодромного устройства с большой постоянной времени образует систему, динамические качества которой могут оказаться сравнительно низкими. Это объясняется тем, что введение такого устройства улучшает вид амплитудной характеристики только в низкочастотной области (рис. 9.6). В результате коэффициенты ошибки, следующие за тем коэффициентом, который обращается в нуль, могут не только не уменьшиться, но даже возрасти.
 .,. сильно возрастают. .,. сильно возрастают.
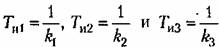 можно сохранить можно сохранить
практически те же условия устойчивости, что и в исходной системе.
Управление но производным от ошибки. В большинстве случаев управление по производным от ошибки имеет целью повысить запас устойчивости системы, что позволяет увеличить

коэффициент передачи разомкнутой системы и тем самым улучшить точность. Это будет рассмотрено более подробно в главе 10.
Однако управление по производным от ошибки может самостоятельно повышать точность системы даже в том случае, когда сохраняется неизменным коэффициент передачи. Физика этого явления заключается в том, что при введении управления но производным система начинает чувствовать не только наличие ошибки, но и тенденцию к изменению ее величины. В результате она более быстро реагирует на появление задающих и возмущающих воздействий, что снижает ошибку.
Структурная схема введения производной по ошибке изображена па рис. 9.8.Не-редаточная функция части прямого канала вместе с включенным дифференцирующим элементом может быть представлена приближенно (в предположении, что дифференцирующий элемент является идеальным) в виде

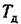 — постоянная времени дифференцирующей цепи. — постоянная времени дифференцирующей цепи.
В качестве дифференцирующих элементов могут, например, применяться устройства, изображенные на рис, 4.20 и 4.21.
Рассмотрим в качестве примера ту же следящую систему (рис. 6.4). При введений производной от ошибки при помощи тахогенераторов, установленных на командно и исполнительной осях, электромеханическая схема будет иметь вид, изображенные па рис. 9.9. Здесь приняты следующие обозначения: СКВТ — синусно-косинуены* вращающиеся трансформаторы, ТГ — тахогеиераторы, Д — двигатель, Р — редуктор
Передаточная функция разомкнутой системы может быть получена умножени ем (9.1) на передаточную функцию (9.21). В результате получим


где постоянная времени 7^ представляет собой отношение передаточного коэффициент тахогеператора к передаточному коэффициенту чувствительного элемента (СКВТ), т. е.

 по ошибке: по ошибке:
 система не будет иметь установившейся ошибки, пропорциональной ускорению. система не будет иметь установившейся ошибки, пропорциональной ускорению.
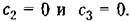 В этом случае можно показать, что в системе, наряду с управлением по первой производной от ошибки, будет использоваться управление по второй производной. Это вытекает из того, что передаточная функция двух дифференцирующих элементов, включенных друг за другом в соответствии с рис. 9.8, будет равна произведению двух передаточных функций типа (9.21): В этом случае можно показать, что в системе, наряду с управлением по первой производной от ошибки, будет использоваться управление по второй производной. Это вытекает из того, что передаточная функция двух дифференцирующих элементов, включенных друг за другом в соответствии с рис. 9.8, будет равна произведению двух передаточных функций типа (9.21):

 представляет собой отношение коэффициентов передачи по первой представляет собой отношение коэффициентов передачи по первой
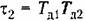 — отношение коэффициентов передачи по — отношение коэффициентов передачи по
второй производной и по ошибке.
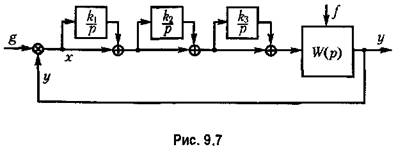
Как видно из рассмотренного, в отличие от случая введения изодромного устройства (см. рис. 9.4), когда обращается в нуль первый, ранее отличный от нуля коэффициент ошибки, введение дифференцирующего элемента (рис. 9.8) не влияет на этот коэффициент ошибки, по зато уменьшает последующие коэффициенты. В связи с этим наиболее эффективное снижение ошибки системы может быть достигнуто при одновременном использовании изодромных устройств и дифференцирующих элементов.
Так как дифференцирование эквивалентно дополнительному усилению верхних частот, то использование более чем двух дифференцирующих элементов оказывается затруднительным вследствие возрастания влияния высокочастотных помех. Число же изодромных устройств ограничивается только получающимся усложнением системы. Однако и оно обычно не превышает трех.
|