Теория систем автоматического управленияДиаграмма вышнеградского
Рассмотрим характеристическое уравнение третьего порядка
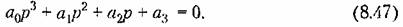
 и введем новую переменную и введем новую переменную

Здесь использовано понятие среднегеометрического корня (8.26):
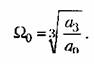
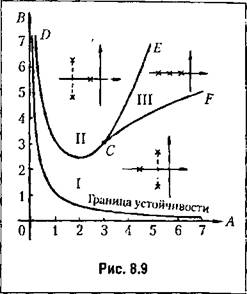
 получим нормированное уравнение где коэффициенты получим нормированное уравнение где коэффициенты

называются параметрами Вышнеградского.

 Это есть равнобокая гипербола, для которой оси координат служат асимптотами (рис. 8.9). Область устойчивости системы, согласно написанным выше условиям, лежит выше этой кривой. Это есть равнобокая гипербола, для которой оси координат служат асимптотами (рис. 8.9). Область устойчивости системы, согласно написанным выше условиям, лежит выше этой кривой.
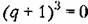


В общем случае возможны два варианта: 1) все три корня вещественные; 2) один корень вещественный и два комплексных.
Граница между этими двумя случаями определяется равенством нулю дискриминанта уравнения третьей степени (8.49), который может быть получен, например, из формулы Кардана для решения кубического уравнения

Это уравнение дает на плоскости параметров Л, В две кривые: СЕ CF (рис. 8.9). Внутри области ЕСF дискриминант положителен. Следовательно, в этой области имеется три вещественных корня (область III). В остальной части плоскости дискриминант отрицателен, что соответствует наличию пары комплексных корней.
 Тогда характеристическое уравнение (8.49) будет Тогда характеристическое уравнение (8.49) будет


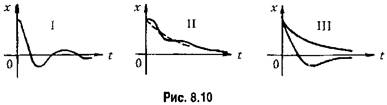
Уравнивание коэффициентов при одинаковых степенях дает
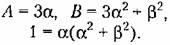
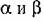 искомое уравнение, соответствующее граничному случаю: искомое уравнение, соответствующее граничному случаю:

Написанное равенство дает на плоскости параметров кривую СП.
В результате область устойчивости разбивается натри части: I, II, III (см. рис. 8.9), Этот график называется диаграммой Вышпеградского. Он построен им в 1876 году в работе, которая положила начало развитию теории автоматического управления. На рисунке показан характер расположения корней внутри каждой из этих частей области устойчивости.
В области III, где все корни вещественные, в зависимости от начальных условий получим апериодический переходный процесс в одной из форм, показанных па третьем графике рис. 8.10. Область III носит название области апериодических процессов.
В областях I и II, где имеется один вещественный корень и два комплексных, переходный процесс будет иметь соответственно формы, показанные на первых двух графиках рис. 8,10. В области I быстрее затухает экспонента и переходный процесс в основном будет определяться колебательной составляющей. Это будет область колебательных процессов. В области II, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов.
Диаграмма Вышнеградского получила дальнейшее развитие. Для более точной оценки характера переходного процесса на ней можно нанести вспомогательные линии, разбивающие области I, II и III на еще более мелкие части, что позволит иметь более полное суждение о быстродействии и запасе устойчивости. Ниже будут рассмотрены наиболее распространенные способы уточнения диаграммы Вышнеградского посредством нанесения линий равной степени устойчивости (для оценки быстродействия) и линий равного затухания (для оценки запаса устойчивости).
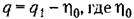 обозначает степень устойчивости для нормированного уравнения. Для исходного уравнения (8.47) согласно (8.48) степень устойчивости будет обозначает степень устойчивости для нормированного уравнения. Для исходного уравнения (8.47) согласно (8.48) степень устойчивости будет



Коэффициенты этого уравнения:

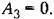 Первое условие при подстановке значений коэффициентов приводит к уравнению Первое условие при подстановке значений коэффициентов приводит к уравнению



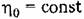 в области I, так как там, согласно рис. 8.9, ближайшими к мнимой оси являются комплексные корни. Кривая г|0 = 0 совпадает с границей устойчивости. Уравнение (8.52) дает прямые, которые нанесены в областях 13 и III. в области I, так как там, согласно рис. 8.9, ближайшими к мнимой оси являются комплексные корни. Кривая г|0 = 0 совпадает с границей устойчивости. Уравнение (8.52) дает прямые, которые нанесены в областях 13 и III.
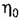 = 0,5. = 0,5.
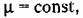 так как колебательность и затухание связаны между собой формулами (8.41) и (8.42). так как колебательность и затухание связаны между собой формулами (8.41) и (8.42).
|