Теория систем автоматического управленияСистемы с амплитудно-импульсной модуляцией
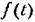 здесь не показано. здесь не показано.
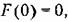 то это всегда возможно. Для преобразованной схемы можно определить передаточную функцию приведенной линейной непрерывной части системы (14.60) или (14.61) то это всегда возможно. Для преобразованной схемы можно определить передаточную функцию приведенной линейной непрерывной части системы (14.60) или (14.61)

и найти соответствующее ей разностное уравнение (4.11), Если его дополнить разностным уравнением нелинейного звена

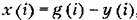 , то получим систему разностных уравнений для замкнутой системы. Решая эти уравнения последовательно шаг за шагом при заданных внешних воздействиях и начальных условиях можно сравнительно просто исследовать процессы в системе. , то получим систему разностных уравнений для замкнутой системы. Решая эти уравнения последовательно шаг за шагом при заданных внешних воздействиях и начальных условиях можно сравнительно просто исследовать процессы в системе.
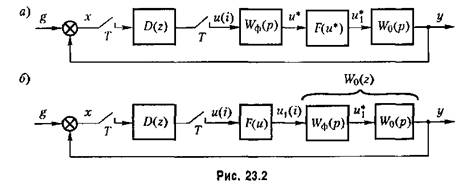
Пример 1. Пусть передаточная функция непрерывной части системы
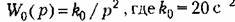 . Период дискретности Т= 0,1 с. Передаточная функция приведенной непрерывной части системы (23.2) имеет вид . Период дискретности Т= 0,1 с. Передаточная функция приведенной непрерывной части системы (23.2) имеет вид
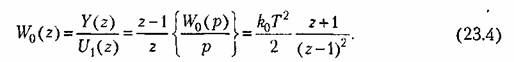
Для коррекции динамических свойств системы применено дискретное корректирующее устройство, передаточная функция которого

Нелинейное звено имеет релейную характеристику с зоной нечувствительности:
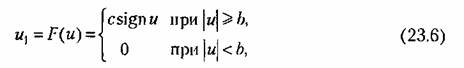
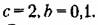
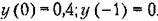
Запишем разностные уравнения, соответствующие (23.4) - (23.6):
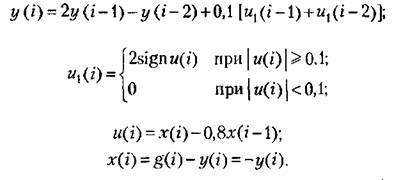
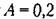 и периодом, равным и периодом, равным
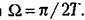
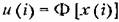
Для исследования устойчивости нелинейных систем с амплитудно-импульсной модуляцией можно использовать частотный метод В. М. Попова и метод гармонической линеаризации.
Первый из них (см. § 17.3) применительно
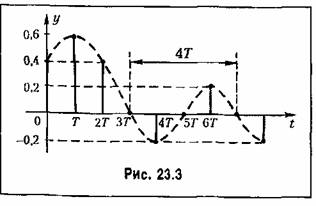
к дискретным системам имеет лишь ту особенность, что передаточной функцией линейной части системы (см. рис. 23.2, б) будет
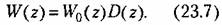 и замену (14.99). Тогда и замену (14.99). Тогда
и условие (17.86) примет вид
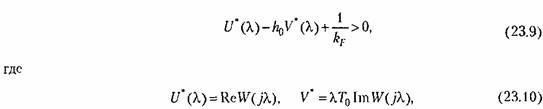
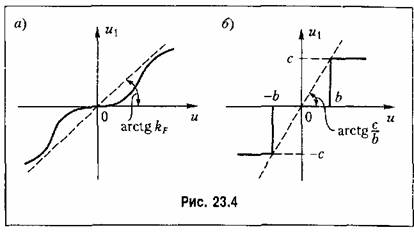
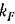 определяет левую границу сектора, к которому принадлежит характеристика нелинейного звена (рис. 23.4). определяет левую границу сектора, к которому принадлежит характеристика нелинейного звена (рис. 23.4).
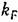 отнести к линейной части системы, то вместо (23.9) получим: отнести к линейной части системы, то вместо (23.9) получим:
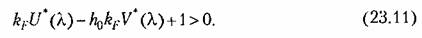
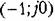 , чтобы вся кривая , чтобы вся кривая
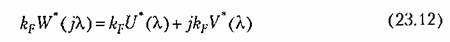
лежала справа от этой прямой.
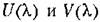 проще находить но известным формулам: проще находить но известным формулам:
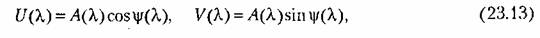
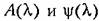 — модуль и аргумент частотной передаточной функции (23.8). В этом — модуль и аргумент частотной передаточной функции (23.8). В этом
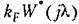 определяется следующим образом: определяется следующим образом:
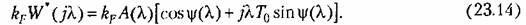
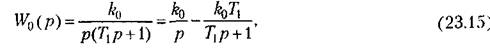
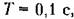 характеристика характеристика
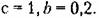
Отметим, что непрерывная система с передаточной функцией линейной части (23.15) и данной характеристикой нелинейного звена устойчива, так как характеристика
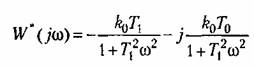
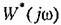 . Этот вывод совпадает . Этот вывод совпадает
с полученным в § 17.1 (пример 3, рис. 17.3, в).
Для исследования дискретной системы находим передаточную функцию (237):
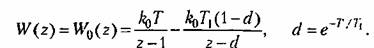
Соответствующая ей частотная передаточная функция (23.8)
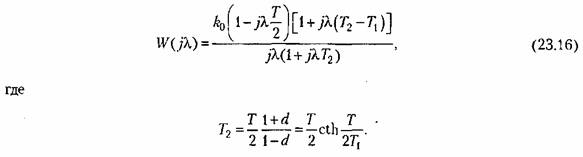
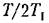 значительно меньше единицы. значительно меньше единицы.
Поэтому приближенно можно принять
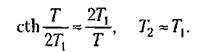
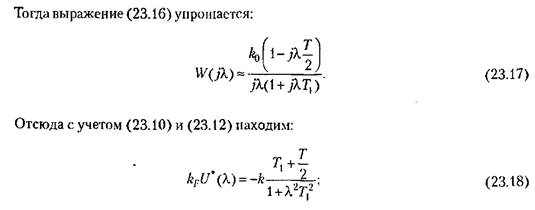
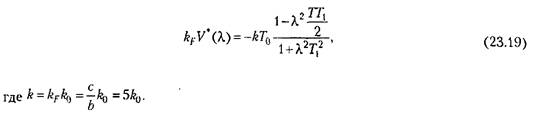
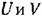 пунктирной пунктирной
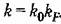 Обе характеристики пересекают ось абсцисс при значении псевдочастоты Обе характеристики пересекают ось абсцисс при значении псевдочастоты
 ) )
на расстоянии кТ/2 от начала координат.
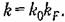
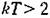 нелинейная дискретная система может стать неустойчивой. Для под- нелинейная дискретная система может стать неустойчивой. Для под-
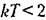 не гарантирует устойчивость системы при наличии внешних воздействий. не гарантирует устойчивость системы при наличии внешних воздействий.
Метод гармонической линеаризации при его применении для исследования нелинейных дискретных систем в значительной степени утрачивает свои ценные качества. Рассмотрим основы этого метода.
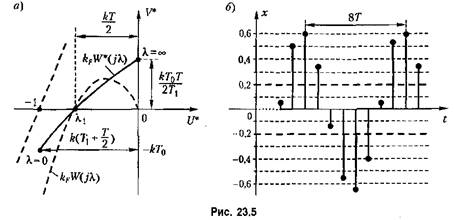
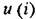 изменяются но гармоническому закону: изменяются но гармоническому закону:
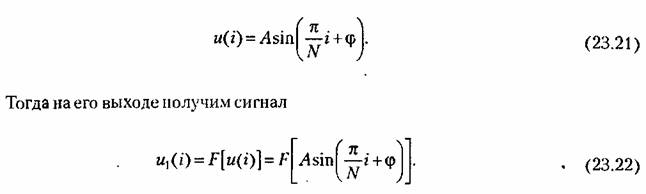
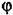 сигнала (23.21). Например, если характеристика нелинейного звена идеальная релейная (см. рис. 23.4, б при Ь = 0), т. е. сигнала (23.21). Например, если характеристика нелинейного звена идеальная релейная (см. рис. 23.4, б при Ь = 0), т. е.

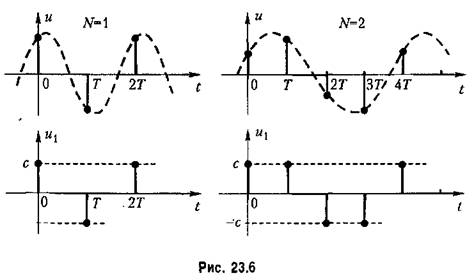
то (рис. 23.6) при N - 1 фаза может изменяться от 0 до я, при N = 2 — от 0 до я/2, а в общем случае

Последовательность (23.22) не может быть представлена рядом Фурье, как это делалось в § 18.1 для непрерывных функций. Поэтому воспользуемся формулами Бесселя для приближенного гармонического анализа. Выделив в получающейся при этом
 тригонометрической сумме слагаемые с частотой (23.1), соответствующие первой гармонике, получим: тригонометрической сумме слагаемые с частотой (23.1), соответствующие первой гармонике, получим:
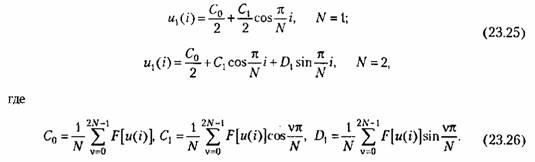
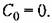 В качестве примера определим коэффициенты гармонической линеаризации для нелинейности (23.23). В соответствии с рис. 23.6 по формулам (23.26) находим: В качестве примера определим коэффициенты гармонической линеаризации для нелинейности (23.23). В соответствии с рис. 23.6 по формулам (23.26) находим:

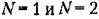 выражение (23.29) является точным. выражение (23.29) является точным.
Из (23.21) и (23.29), используя символическую запись
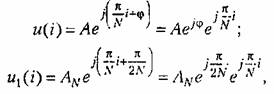
с учетом (23.24) определяем коэффициент гармонической линеаризации
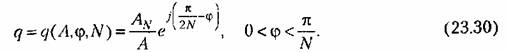
В отличие от (18.18) он зависит не только от амплитуды Л, пои отфи N.
Далее для определения периодических режимов можно было бы использовать способы, аналогичные рассмотренным в § 18.2. Однако даже в данном случае при простейшей характеристике нелинейного звена этот процесс оказывается трудоемким. Кроме того, для других и ел инейиостей при получении коэффициентов гармонической линеаризации возникают большие сложности.
Вместе с тем в ряде случаев исследование периодических режимов можно произвести более простым способом.
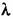 (14.100), значения которой на фиксированных частотах (23.1) (14.100), значения которой на фиксированных частотах (23.1)
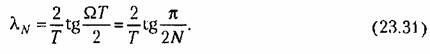
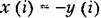 и на входе нелинейного звена образуется сигнал и на входе нелинейного звена образуется сигнал
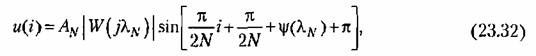
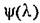 ■- ее ■- ее
аргумент.
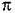 вносится сравнивающим устройством. Сопоставив (23.32) с(23.21) сразу получим : вносится сравнивающим устройством. Сопоставив (23.32) с(23.21) сразу получим :
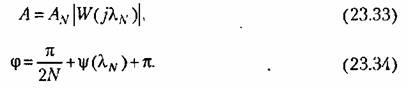
Так как фаза ф может изменяться в пределах (23.24) то
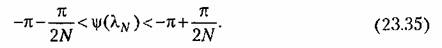
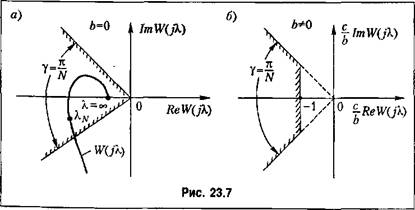
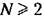 может существовать, если может существовать, если
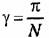
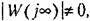 т. е. если АФХ закапчивается на оси абсцисс. т. е. если АФХ закапчивается на оси абсцисс.
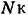 другому. другому.
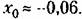
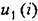 может принимать лишь два фиксированных значения: +сили -с. может принимать лишь два фиксированных значения: +сили -с.
 кроме фазового условия (23.35) должно выполняться дополнительное амплитудное условие кроме фазового условия (23.35) должно выполняться дополнительное амплитудное условие

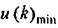 — минимальная из ординат последовательности (23.21): — минимальная из ординат последовательности (23.21):
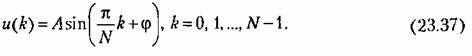
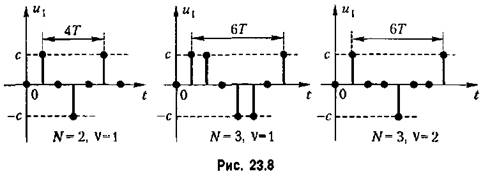
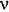 из ординат (23.37) при V < N - 1 условие (23.36) не выполняется, то соответствующие значения последовательности и} (г) становятся равными нулю (рис. 23.8). из ординат (23.37) при V < N - 1 условие (23.36) не выполняется, то соответствующие значения последовательности и} (г) становятся равными нулю (рис. 23.8).
Тогда по формулам (23.25) и (23.26) вместо (23.28) получим:
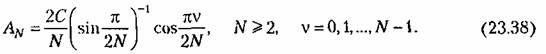
Выражение (23.28) представляет собой частный случай (23.38) при V - 0. , Последовательность па выходе пел инейиого звена
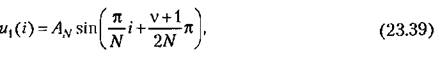

совпадающие с (23.35).
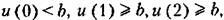 где ординаты и (к) определяются по где ординаты и (к) определяются по
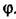
Во многих случаях вопрос об отыскании периодических режимов не ставится. Наоборот, может быть поставлена задача так синтезировать систему чтобы исключить возможность появления этих режимов, что часто (см. гл. 18) гарантирует обеспечения устойчивости системы.
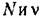 невозможны, если не невозможны, если не
выполняются фазовое условие (23.42) или сформулированные выше амплитудные условия. Можно показать, что это с некоторым запасом обеспечивается, если АФХ
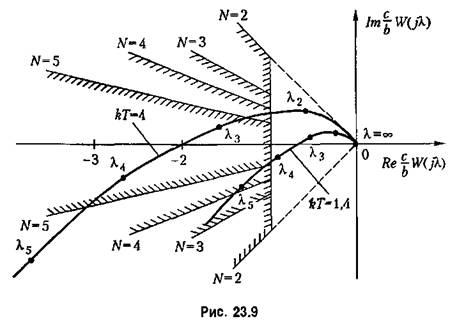
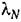 не попа дает в запретную область, изображенную на рис. 23.7, б. не попа дает в запретную область, изображенную на рис. 23.7, б.
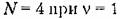 показан на рис. 23.5, б. показан на рис. 23.5, б.
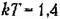 периодические режимы отсутствуют, а система устойчива. периодические режимы отсутствуют, а система устойчива.
Методы исследования нелинейных дискретных систем с амплитудно-импульсной модуляцией рассмотрены также в работах [8.27,49,73,79, 97] и др.
|