Теория систем автоматического управленияЧастотная передаточная функция и частотные характеристики
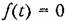 , а на входе имеется гармоническое воздействие , а на входе имеется гармоническое воздействие
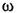 — угловая частота этого воздействия. — угловая частота этого воздействия.
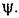 Таким образом, для выходной величины можно записать Таким образом, для выходной величины можно записать
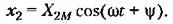
Воспользуемся формулой Эйлера и представим входную и выходную величины в виде суммы экспоненциальных функций:
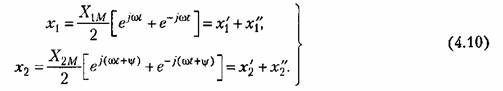
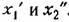 . Кроме того, можно легко показать, . Кроме того, можно легко показать,
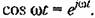 Тогда Тогда
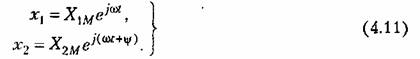
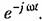
Для нахождения соотношения между входной и выходной гармоническими величинами звена воспользуемся его дифференциальным уравнением в виде
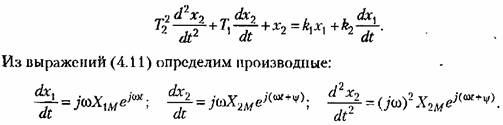
Подставив значения входной и выходной величин и их производных в дифференциальное уравнение, получим:
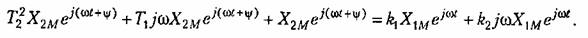
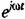 найдем: найдем:
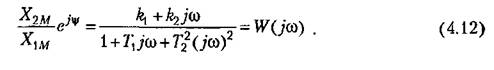
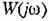 представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент — сдвигу фаз выходной величины по отношению к входной: представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент — сдвигу фаз выходной величины по отношению к входной:
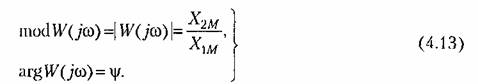
В более общей формулировке для входного сигнала любого вида частотную передаточную функцию можно представить как отношение изображений (частотных изображений) выходной и входной величии:
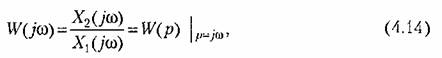
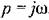
Частотная передаточная функция звена есть изображение Фурье его функции веса, т. е. имеет место интегральное преобразование

Частотная передаточная функция может быть представлена в следующем виде:
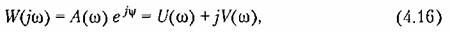
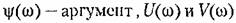
вещественная и мнимая составляющие частотной передаточной функции.
Модуль частотной передаточной функции находится как отношение модулей числителя и знаменателя. Для рассмотренного выше выражения (4.12)
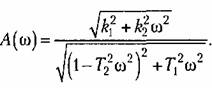
Аргумент или фаза частотной передаточной функции находится как разность аргументов числителя и знаменателя. Для (4.12) имеем:
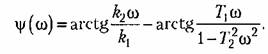
Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе путем умножения числителя и знаменателя на комплексную величину, сопряженную знаменателю, и затем произвести разделение на вещественную и мнимую части. Для (4.12)
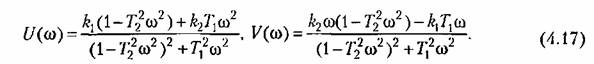
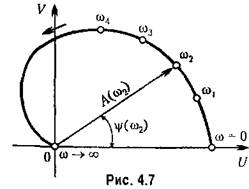
Для наглядного представления частотных свойств звена используются так называемые частотные характеристики.
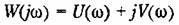
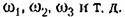
Длина вектора, проведенного из начала координат в точку а. ф. х., соответствующую какой-то выбранной частоте, равна модулю частотной передаточной функции. Угол между вектором и положительным направлением вещественной оси, отсчитываемый против часовой стрелки, равен аргументу или фазе частотной передаточной функции. Таким образом, а. ф. х, дает возможность наглядно представить для каждой частоты входного воздействия звена отношение амплитуд выходной и входной величин и сдвиг фаз между ними.
Построение а. ф. х. по вещественной и мнимой частям частотной передаточной функции, как правило, является трудоемкой работой, так как умножение частотной передаточной функции на комплексную величину, сопряженную ее знаменателю, повышает в два раза степень частоты в знаменателе. Обычно гораздо проще строить а. ф. х., используя полярные координаты, т. е. вычисляя непосредственно модуль и фазу. Зная модуль и фазу, можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости при известных модуле и фазе легко вычислить вещественную и мнимую части умножением модуля па направляющий косинус между вектором и соответствующей осью.
Вместо а. ф. х. можно построить отдельно амплитудно-частотную характеристику (а. ч. х.) и фазочастотпую характеристику (ф, ч. х.).
Амплитудно-частотная характеристика показывает, как пропускает звено сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин. Фазочастотиая характеристика показывает фазовые сдвиги, вносимые звеном па различных частотах,
Как следует из сказанного выше, модуль частотной передаточной функции представляет собой четную функцию частоты, а фаза— нечетную функцию частоты.
 Логарифмические частотные характеристики Логарифмические частотные характеристики
Логарифмические частотные характеристики ( л. ч. х.) включают в себя построенные отдельно на одной плоскости логарифмическую амплитудную характеристику (л. а. х.) и логарифмическую фазовую характеристику (л. ф. х.). Для построения л. а. х. находится величина
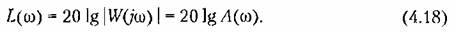
Эта величина выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Один Бел соответствует увеличению мощности в 10 раз, 2 Бела — в 100 раз, 3 Бела — в 1000 раз и т. д.
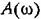 представляет собой отношение не мощностей, а выходной и входной величин (перемещений, скоростей, напряжений, токов и т. п.), то увеличение этого отношения в десять раз будет соответствовать увеличению отношения мощностей в сто раз, что соответствует двум Белам или двадцати децибелам. Поэтому в правой части (4.19) стоит множитель 20. представляет собой отношение не мощностей, а выходной и входной величин (перемещений, скоростей, напряжений, токов и т. п.), то увеличение этого отношения в десять раз будет соответствовать увеличению отношения мощностей в сто раз, что соответствует двум Белам или двадцати децибелам. Поэтому в правой части (4.19) стоит множитель 20.
Необходимость логарифмировать модуль частотной передаточной функции (4.18) приводит к тому, что, строго говоря, л. а. х. может быть построена только для тех звеньев, у которых передаточная функция представляет собой безразмерную
величину. Это возможно при одинаковых размерностях входной и выходной величин звена. В дальнейшем изложении будет подразумеваться именно этот случай.
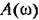 понимается отношение модуля частотной передаточной функции к этой исходной единице. понимается отношение модуля частотной передаточной функции к этой исходной единице.
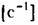 и которую приходится логарифмировать в соответствии с изложенным. и которую приходится логарифмировать в соответствии с изложенным.
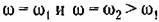
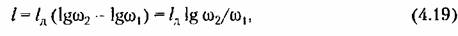
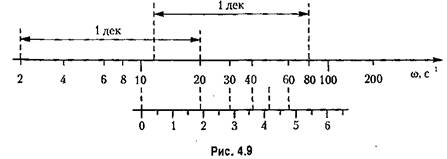
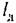 — желаемая длина одной декады. — желаемая длина одной декады.
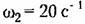
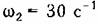 на расстоянии 60 1§ 3 - 29 мм и т. д. на расстоянии 60 1§ 3 - 29 мм и т. д.
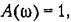 так как логарифм единицы равен нулю. так как логарифм единицы равен нулю.
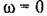 лежит на оси частот слева в бесконечности, так как лежит на оси частот слева в бесконечности, так как
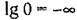 , Поэтому ось ординат проводят так, чтобы справа от нее можно было показать весь ход л. а. х. Как будет показано ниже, для этой цели необходимо провести ось ординат левее самой малой сопрягающей частоты л. а. х. , Поэтому ось ординат проводят так, чтобы справа от нее можно было показать весь ход л. а. х. Как будет показано ниже, для этой цели необходимо провести ось ординат левее самой малой сопрягающей частоты л. а. х.
Для построения л. ф. х. используется та же ось абсцисс (ось частот). По оси ординат откладывается фаза в градусах в линейном масштабе. Для практических расчетов, как это будет ясно ниже, удобно совместить точку нуля децибел с точкой, где фаза равна -180°. Отрицательный сдвиг но фазе откладывается по оси ординат вверх, а положительный — вниз.
Главным достоинством логарифмических амплитудных частотных характеристик является возможность построения их во многих случаях практически без вычислительной работы. Это особенно проявляется в тех случаях, когда частотная передаточная функция может быть представлена в виде произведения сомножителей. Тогда результирующая л, а. х. может быть приближенно построена в виде так называемой асимптотической л. а. х представляющей собой совокупность отрезков прямых линий с наклонами, кратными величине 20 дБ/дек. Это будет показано ниже при рассмотрении конкретных звеньев.
Для иллюстрации простоты построения л. а. х. рассмотрим несколько важных примеров.
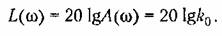
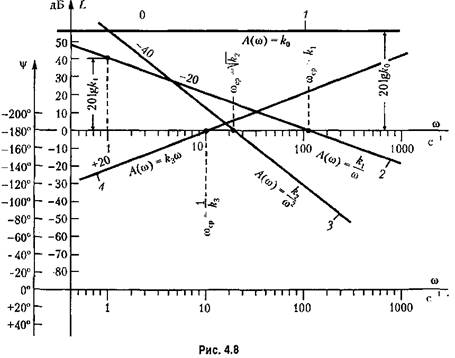
Л. а. х. представляет собой прямую, параллельную оси абсцисс (прямая 1 на рис. 4.8).
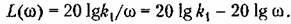
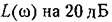 (прямая 2 на рис. 4.8). (прямая 2 на рис. 4.8).
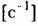
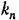 должна быть [с n]. должна быть [с n].
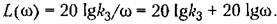
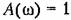 (прямая 4 на рис. 4.8). (прямая 4 на рис. 4.8).
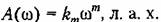 представляет собой прямую линию с положительным наклоном т 20 дБ/дек. Эта прямая также может быть построена но одной какой-либо точке, например по точке представляет собой прямую линию с положительным наклоном т 20 дБ/дек. Эта прямая также может быть построена но одной какой-либо точке, например по точке
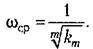
|