Теория систем автоматического управленияПрохождение медленно меняющихся сигналов в автоколебательных системах
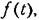 которое может быть либо возмущающим, либо управляющим (задающим), в автоколебательной системе является не постоянным, а медленно меняющимся. Медленно меняющейся будем называть такую функцию времени, которая сравнительно мало изменяется за период автоколебаний, т. с, соблюдается условие в виде одного из неравенств которое может быть либо возмущающим, либо управляющим (задающим), в автоколебательной системе является не постоянным, а медленно меняющимся. Медленно меняющейся будем называть такую функцию времени, которая сравнительно мало изменяется за период автоколебаний, т. с, соблюдается условие в виде одного из неравенств

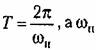 — частота автоколебаний, — частота автоколебаний,
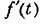 будет такая, для которой выполняется условие будет такая, для которой выполняется условие
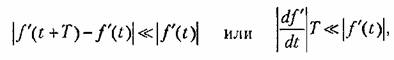
Указанными свойствами почти всегда обладают полезные сигналы управления, проходящие через автоматическую автоколебательную систему (в том числе в переходных процессах).
Условие медленного изменения любой функции времени можно выразить также и в частотной форме, а именно: медленно меняющейся считается такая функция, возможные частоты изменения которой во времени значительно ниже возможной частоты возникающего в системе периодического решения (автоколебаний).
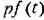
считать постоянной за время каждого периода исследуемых автоколебаний и искать решение в той же форме (19.4):

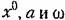 будут не будут не
 будет медленно меняющимся сигналом на входе нелинейности. будет медленно меняющимся сигналом на входе нелинейности.
В связи со сказанным здесь остается в силе разложение (19.5) - (19.7). Но подстановка его в заданное уравнение нелинейной автоматической системы (19.1) дает

 , данное уравнение может быть , данное уравнение может быть
разделено на два отдельных уравнения:

соответственно для медленно меняющейся составляющей и для колебательной составляющей. При этом разделении уравнений, как и прежде, сохраняются существенно нелинейные свойства системы.
 (на фоне автоколебаний системы) в виде (на фоне автоколебаний системы) в виде

Таким образом, получается, что для определения медленно меняющихся процессов функцию смещения


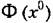 представляет собой как бы статическую характеристику (обычно криволинейную), которая определяет зависимость между выходной и входной величинами заданной нелинейности для постоянных или медленно меняющихся сигналов в автоколебательной системе. представляет собой как бы статическую характеристику (обычно криволинейную), которая определяет зависимость между выходной и входной величинами заданной нелинейности для постоянных или медленно меняющихся сигналов в автоколебательной системе.
 может получать при определенных условиях вид весьма плавной кривой. Этот может получать при определенных условиях вид весьма плавной кривой. Этот

 можно называть сглаженной нелинейной характеристикой. можно называть сглаженной нелинейной характеристикой.
Так, в примере § 19.1 согласно (19.40) функция смещения будет иметь вид рис. 19.6, а, т, е. для медленно меняющегося сигнала в данной релейной системе нелинейная характеристика будет в определенных пределах иметь плавный вид (рис. 19.6, а) вместо скачкообразного (рис. 19.6, б) — за счет сглаживающего влияния автоколебательных вибраций.
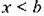 при отсутствии при отсутствии
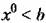
 без зоны нечувствительности (рис. 19.7, б). Эффект вибрационного сглаживания нелинейностей в этих примерах является положительным (ликвидация зон нечувствительности и петель). без зоны нечувствительности (рис. 19.7, б). Эффект вибрационного сглаживания нелинейностей в этих примерах является положительным (ликвидация зон нечувствительности и петель).
 будет меньше, чем само значение F, соответствующее линейному начальному участку. Поэтому постоянный или медленно меняющийся сигнал будет при наличии автоколебаний проходить через данную нелинейность с меньшим коэффициентом усиления, чем без автоколебаний, что может в известных случаях отрицательно сказаться на качестве автоматической системы в целом. будет меньше, чем само значение F, соответствующее линейному начальному участку. Поэтому постоянный или медленно меняющийся сигнал будет при наличии автоколебаний проходить через данную нелинейность с меньшим коэффициентом усиления, чем без автоколебаний, что может в известных случаях отрицательно сказаться на качестве автоматической системы в целом.


 будет будет
необходимо только с точки зрения проверки выполнения условий вибрационного сглаживания нелинейности и допустимости таких вибраций в данной конкретной автоматической системе. Основными же для качества работы автоматической системы при этом будут являться медленно меняющиеся процессы, определяемые уравнением (19.68). С точки зрения упрощения их определения весьма важными являются следующие два обстоятельства.
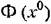 зависит от формы нелинейности, от структуры и от параметров системы. зависит от формы нелинейности, от структуры и от параметров системы.
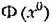 при любых частных упрощающих предположениях относительно внешних воздействий. Можно, например, пользоваться более простым вторым методом из описанных в § 19.1 методов и проиллюстрированных там на примере, взяв любое одно постоянное по величине внешнее воздействие. при любых частных упрощающих предположениях относительно внешних воздействий. Можно, например, пользоваться более простым вторым методом из описанных в § 19.1 методов и проиллюстрированных там на примере, взяв любое одно постоянное по величине внешнее воздействие.
 получает вид плавной кривой. получает вид плавной кривой.
Поэтому, в отличие от первоначально заданной нелинейности, ее легко можиолинеа ризовать обычным способом (по касательной или по секущей в начале координат или в другом начале отсчета). Имея в виду это свойство, часто вместо термина вибрационное сглаживание употребляют термин вибрационная линеаризация (будем придерживаться первого из них).
Итак, в определенном диапазоне можно считать

 зависит от соотношения, вообще говоря, от всех параметров системы. зависит от соотношения, вообще говоря, от всех параметров системы.
Например, для системы, описываемой уравнениями (19.20) - (19.23), согласно (19.53) и (19.50) имеем

Поэтому для расчета медленно протекающих процессов в данной системе па основании (19.20) - (19.22) и (19.70) получаем линейные уравнения:

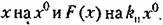
 определяется согласно (19.13) и определяется согласно (19.13) и
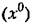 , то , то
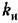 можно представить в виде можно представить в виде
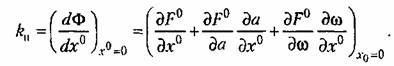
 не зависит от со и, кроме того, согласно (19.6) не зависит от со и, кроме того, согласно (19.6)

 как однозначных, так и петлевых, как однозначных, так и петлевых,
 можно вычислять по формуле можно вычислять по формуле

 . Во многих задачах это будет существенным упрощением решения. . Во многих задачах это будет существенным упрощением решения.
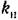 приходится определять не по касательной, а по секущей. приходится определять не по касательной, а по секущей.
Итак, с подстановкой (19.70) уравнение (19.68) для определения медленно протекающих процессов становится обыкновенным линейным уравнением
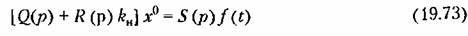
и, как таковое, легко решается.

 чем чем
 ). ).
Особенно важно использовать свойство вибрационного сглаживания нелинейностей с последующей их обычной линеаризацией при расчете сложных автоматических систем.
 не удается сделать малой (тогда руль будет колебаться), то необходимо, чтобы указанная частота практически не воспринималась корпусом самолета в процессе его движения вокруг центра тяжести. не удается сделать малой (тогда руль будет колебаться), то необходимо, чтобы указанная частота практически не воспринималась корпусом самолета в процессе его движения вокруг центра тяжести.
Тогда расчет автоматической системы будет выглядеть следующим образом.
 При этом следим затем, чтобы частота автоколебаний системы (зависящая от параметров системы) лежала за пределами частот возможных колебаний самолета (чтобы она практически не воспринималась корпусом самолета). При этом следим затем, чтобы частота автоколебаний системы (зависящая от параметров системы) лежала за пределами частот возможных колебаний самолета (чтобы она практически не воспринималась корпусом самолета).
 . .
 , зависящим от автоколебаний, т. е. от параметров внутреннего контура системы). Если необходимо учесть неременные коэффициенты и нелинейности самого самолета, то уравнения системы в целом не будут уже столь простыми. Однако и в этом случае полностью сохраняет смысл предварительный отдельный расчет внутреннего контура системы, так как влияние нелинейностей самого самолета будет распространяться обычно только нате процессы движения, которые по сравнению с автоколебаниями внутреннего контура являются медленными. , зависящим от автоколебаний, т. е. от параметров внутреннего контура системы). Если необходимо учесть неременные коэффициенты и нелинейности самого самолета, то уравнения системы в целом не будут уже столь простыми. Однако и в этом случае полностью сохраняет смысл предварительный отдельный расчет внутреннего контура системы, так как влияние нелинейностей самого самолета будет распространяться обычно только нате процессы движения, которые по сравнению с автоколебаниями внутреннего контура являются медленными.
Известно, что и само движение самолета, например по тангажу, можно, разделить на два, одно более быстрое — движение относительно центра масс (угловое движение) и другое более медленное — движение центра масс (движение но траектории). Оба они являются медленными по сравнению с автоколебаниями внутреннего контура системы управления. Однако их тоже можно рассматривать отдельно. Следовательно, в этом случае, кроме обычно применяемого пространственного разбиения движения самолета по каналам (тангажа, курса, крена), расчет системы по каждому каналу (например, тангажа) разбивается еще натри этапа по степени медленности движения во времени.
Аналогичное разделение расчета по крайней мере на два этапа по степени медленности во времени бывает целесообразным и для многих других нелинейных автоматических систем (слежения, стабилизации и т. п.). В сложных системах такие приемы, существенно упрощающие все исследование, оказываются единственными, которые могут сделать расчет системы практически осуществимым. Важно иметь в виду, что при этом принципе разделения движений сохраняется существенная нелинейная взаимосвязь между ними.
|