Теория систем автоматического управленияМедленно меняющиеся процессы в автоколебательных системах
Статические и скоростные ошибки автоколебательных систем
В предыдущих главах исследовались симметричные автоколебания, как результат свободного движения системы (т. е. без внешнего воздействия) при симметричных нелииейностях. Однако, как будет показано, важное практическое значение имеет также рассмотрение несимметричных автоколебаний.
Несимметрия автоколебаний может вызываться различными причинами: 1) несимметричностью нелинейной характеристики как при наличии, так и при отсутствии внешних воздействий;
, 2) наличием постоянного или медленно меняющегося внешнего воздействия при симметричных пелинейностях;
3) наличием постоянной или медленно меняющейся скорости изменения внешнего воздействия при симметричных нелииейностях (для тех случаев, когда постоянное воздействие не вызывает смещения центра колебаний; обычно это имеет место в следящих системах и вообще в астатических системах).
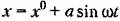 , вследствие чего колебания переменной F становятся несимметричными по амплитуде и но времени (рис. 19.2, а) или только по времени (рис. 19.2, б). , вследствие чего колебания переменной F становятся несимметричными по амплитуде и но времени (рис. 19.2, а) или только по времени (рис. 19.2, б).
Пусть задай а автоматическая система, динамика которой описывается уравнением


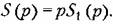
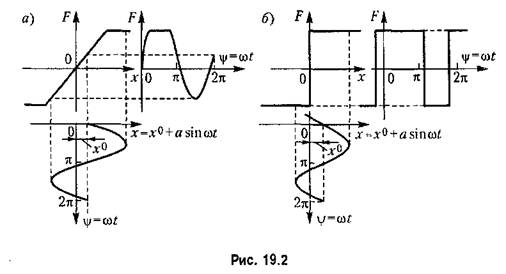
Поэтому запишем уравнение (19.1) в виде

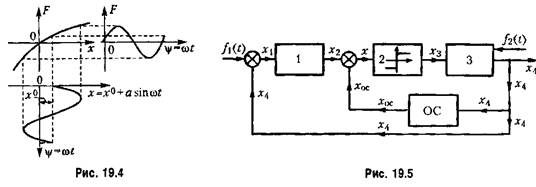
При этом решение нелинейного уравнения (19.1), в отличие от прежнего (§ 18.2), ищется в форме

 со являются неизвестными постоянными. со являются неизвестными постоянными.
С учетом величины смещения х первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде
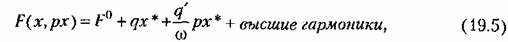
где при обозначении у = сог

Отсюда видно, что в общем случае все три коэффициента являются функциями трех неизвестных:
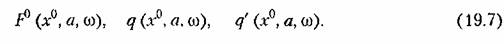
В частных случаях эти зависимости могут быть более простыми. Подстановка выражений (19.4) и (19.5) в заданное дифференциальное уравнение (19.1) с учетом свойства фильтра (см. § 18.2) дает
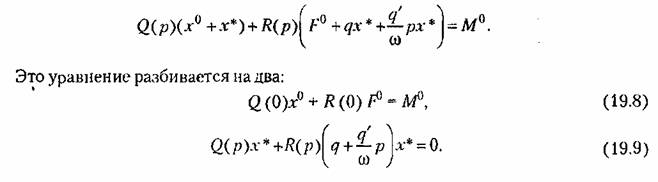
При таком разделении сохраняются существенно нелинейные свойства и отсутствие суперпозиции решений, так как остается нелинейная взаимосвязь обоих уравнений через соотношения (19,7).
Можно предложить два метода решения задачи.
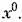 Поэтому, написав как прежде характеристическое уравнение Поэтому, написав как прежде характеристическое уравнение
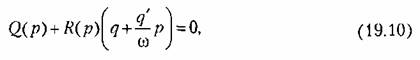
 и выделив вещественную и мнимую части, в отличие от (18.36), полу- и выделив вещественную и мнимую части, в отличие от (18.36), полу-
чим здесь два алгебраических уравнения стремя неизвестными:

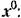

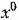 (рис, 19.3). (рис, 19.3).
После того как из уравнений (19.11) определены зависимости (19.12), можно, воспользовавшись первым из выражений (19.7), найти функцию смещения

Подставив ее в (19.8), получим алгебраическое уравнение
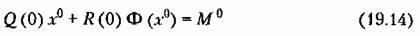
Указанную зависимость (19.12) амплитуды и частоты автоколебаний от величины смещения центра колебаний надо всегда иметь в виду. При одних нелинейностях она может быть весьма существенной, при других — менее существенной.
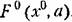


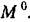
 и является искомой статической или скоростной ошибкой соответственно для статической и астатической систем. и является искомой статической или скоростной ошибкой соответственно для статической и астатической систем.
 вместо (19.14) получаем уравнение вместо (19.14) получаем уравнение


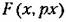 , для которой , для которой
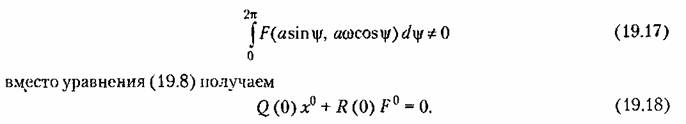
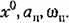

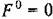 ), как показано, например, па рис. 19.4 в отличие от рис. 19.1,(5. ), как показано, например, па рис. 19.4 в отличие от рис. 19.1,(5.
Приведем пример исследования совместного влияния двух внешних воздействий, причем из дальнейшего будет видно, что, в отличие от линейных систем, здесь нельзя просто складывать статические ошибки от отдельно взятых воздействий.
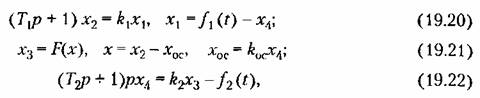 системы (рис. 19.5) заданы в виде системы (рис. 19.5) заданы в виде
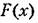 — простейшая симметричная релейная характеристика показанная на рис. 19.5: — простейшая симметричная релейная характеристика показанная на рис. 19.5:

Чтобы воспользоваться выведенными выше общими формулами/надо сначала привести заданную систему уравнений (19.20) - (19.22) к одному уравнению типа (19.1). В результате получаем
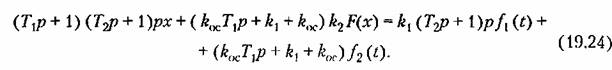

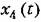
 является возмущающим и является возмущающим и
имеет постоянную величину (например, постоянная нагрузка на выходном валу системы):

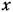 с учетом автоколебаний следует искать в виде с учетом автоколебаний следует искать в виде
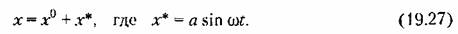
Гармоническая линеаризация нелинейности (19.23) при этом согласно (19.6) дает
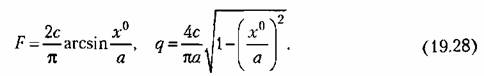

а уравнение (19.8) для постоянных составляющих будет

где согласно (19.24) --.(19.26)

Выше были указаны два метода решения задачи. Для иллюстрации обоих методов решим данную задачу каждым из них.
Характеристическое уравнение здесь будет
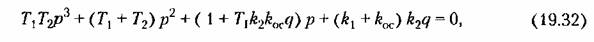
и уравнения (19.11) поэтому примут вид

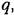 находим частоту автоколебаний находим частоту автоколебаний

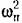 из (19.34), получаем биквадратное уравнение для отыскания зависимости амплитуды автоколебаний ап от смещениях0: из (19.34), получаем биквадратное уравнение для отыскания зависимости амплитуды автоколебаний ап от смещениях0:
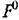 , откуда с использованием (19.39) , откуда с использованием (19.39)
найдем функцию смещения
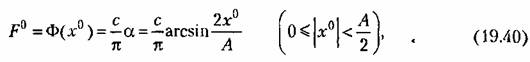
где Л определяется через параметры системы формулой (19.36).
Подставив величину (19.40) в уравнение (19.30) для постоянных составляющих, с учетом (19.31) и (19.36) получим
Из формулы (19.43) видно, что автоколебания существуют до тех пор, пока величины внешних воздействий удовлетворяют условию

 автоколебаний при наличии внешних воздействий. автоколебаний при наличии внешних воздействий.
Проиллюстрируем также и второй метод. Согласно второму методу сначала решается уравнение (19.30). По (19.30) и первой из формул (19.28) находим

Для отыскания входящей сюда амплитуды а воспользуемся уравнением (19.29). Характеристическое уравнение для него будет (19.32), и уравнения (19.11) поэтому
примут вид:

Исключая из уравнений (19.46) величину ц, находим частоту автоколебаний

 в первое из уравнений (19.46), найдем в первое из уравнений (19.46), найдем
амплитуду автоколебаний

является амплитудой автоколебаний при отсутствии внешних воздействии (при
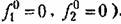 найденное выражение амплитуды (19.49) в формулу (19.45), получим окончательно величину смещения найденное выражение амплитуды (19.49) в формулу (19.45), получим окончательно величину смещения
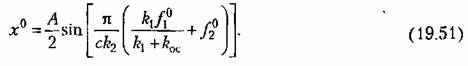
Как видно, второй метод в данной задаче приводит к тем же самым результатам значительно более коротким путем, чем первый, что очень важно для практических расчетов (принципиально же оба метода эквивалентны друг другу). По-видимому, большая простота второго метода будет иметь место и в большинстве других задач.
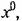
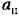 зависящей от них. Подставив значение квадратной скобки из (19.51) в (19.45), получим зависящей от них. Подставив значение квадратной скобки из (19.51) в (19.45), получим

а подставив это в первую из формул (19.28), сразу получим искомую функцию смешения

где Л выражается только через параметры системы согласно (19.50).
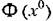 не зависит ни от числа внешних воздействий, ни от характера их изменения (если они постоянные или медленно меняющиеся), что наиболее наглядно было видно из первого метода решения задачи. не зависит ни от числа внешних воздействий, ни от характера их изменения (если они постоянные или медленно меняющиеся), что наиболее наглядно было видно из первого метода решения задачи.
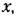 которая уже известна, из заданных уравнений системы (19.20) и (19.21) получаем которая уже известна, из заданных уравнений системы (19.20) и (19.21) получаем
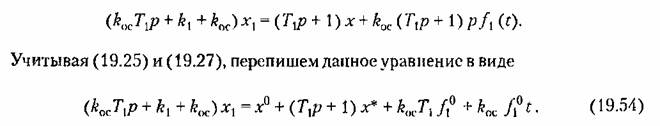
В соответствии с видом правой части установившееся решение этого линейного уравнения следует искать в виде

 — периодическая составляющая. — периодическая составляющая.
Подставив это в (19.54), получим три уравнения для отыскания указанных величин;
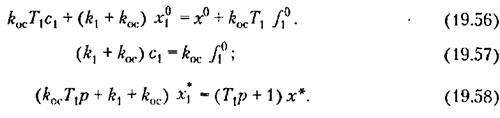
Второе из них дает

Тогда из (19.56) находим
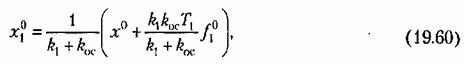
 определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной.: определяется формулой (19.51) через внешние воздействия. Наконец, из уравнения (19.58) получаем амплитуду автоколебаний переменной.:
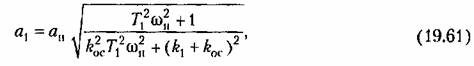
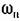 — формулой (19,48). — формулой (19,48).
 согласно (19.59) будет согласно (19.59) будет
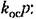
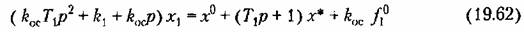
 в отличие от (19.55), будет в отличие от (19.55), будет

При этом из (19.62) находим:
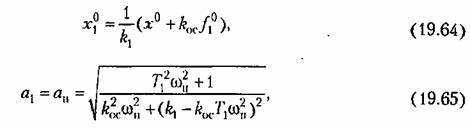
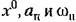 (их можно получить таким же (их можно получить таким же
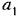 можно сделать весьма малой. можно сделать весьма малой.
|