Вязкость и пластичность нефтепродуктовДвижение жидкости между вращающимся и неподвижным коаксиальными цилиндрами
Большой интерес представляет движение вязкой жидкости, помещенной между двумя вертикальными цилиндрами, имеющими параллельную общую центральную ось и различный диаметр (коаксиальные цилиндры), один из которых вращается, а второй неподвижен (фиг. 26). На этом виде движения жидкости основан второй класс вискозиметров — ротационные вискозиметры или вискозиметры с коаксиальными цилиндрами. Рассмотрим случай, когда вращается внутренний цилиндр, имеющий
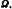 а внешний цилиндр, имеющий радиус г2, а внешний цилиндр, имеющий радиус г2,
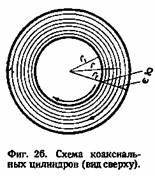
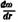 , а , а
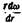 . Если длина рассматриваемого цилиндра Л, то его боковая поверхность 5=2 nrh. Силу трения о соседний, более медленно движущийся цилиндрический слой, найдем подстановкой соответствующих значений в формулу Ньютона: . Если длина рассматриваемого цилиндра Л, то его боковая поверхность 5=2 nrh. Силу трения о соседний, более медленно движущийся цилиндрический слой, найдем подстановкой соответствующих значений в формулу Ньютона:
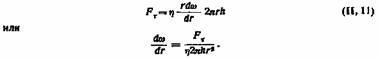
Градиент скорости пропорционален приложенной тангенциальной силе сдвига и обратно пропорционален вязкости, длине цилиндра и квадрату его радиуса.
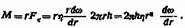 г, находим, что г, находим, что
Поскольку г выбрано произвольно, это выражение равно моменту внешних сил, поддерживающих вращение цилиндра. Интегрируя и перенося г в левую часть равенства, находим
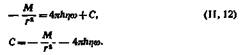
Для r=srx o> = Q и для г = г2 о) = 0, откуда константа интегрирования
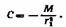
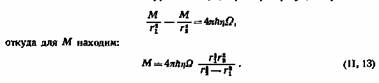 ее значение в уравнение (II, 12) и преобразуя, получаем: ее значение в уравнение (II, 12) и преобразуя, получаем:
Формула (II, 13) применима для вычисления вращательного момента М и для того случая, когда вращается наружный цилиндр, а внутренний неподвижен (например, подвешен на упругой нити). Очевидно
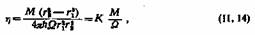
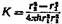 постоянно для каждой пары коаксиальных цилиндров. постоянно для каждой пары коаксиальных цилиндров.
Формулы (II, 13) и (II, 14) справедливы до начала турбулентности. Число Рейнольдса для прибора с коаксиальными цилиндрами
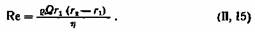
Куэтт нашел для прибора, в котором вращался наружный цилиндр, что турбулентность наступает при Re ~ 1900. В противоположность этому Тэйлор пользуясь установкой аналогичной конструкции, но выполненной более совершенно, не обнаружил турбулентности до Re = 12500. При вращении внутреннего цилиндра турбулентность маловязких жидкостей, по-видимому, наступает значительно раньше, чем при вращении внешнего цилиндра.
При рассмотрении внутреннего трения жидкости между коаксиальными цилиндрами не учитывалось влияние дна цилиндра и его концов. Между тем практически всегда приходится иметь дело с концевыми эффектами. Для устранения или учета этих эффектов предложены различные способы f7, 8]. М- П. Воларович разработал остроумный принцип, заключающийся в присоединении к нижнему концу обоих вертикальных цилиндров полушарий.
Теория движения вязкой жидкости в зазоре между двумя полушариями неодинакового радиуса разработана достаточно подробно и позволяет связывать вязкость жидкости, вращательный момент и угловую скорость . В последнее время созданы специальные ротационные вискозиметры, состоящие из двух полушарий с общим центром и разной длиной радиуса. Испытуемая жидкость помещается в зазор между полушариями .
3. Движение шарика в жидкости. Из других видов движения твердых тел в жидкости мы остановимся на наиболее простом случае—движении недеформируемого шарика под влиянием силы тяжести. Этот случай представляет значительный интерес для вискозиметрии, а также для описания подъема (или падения) шариков эмульсии и газа, падения твердых шарообразных частиц при седимометрическом анализе и т. д.
Математическая теория сопротивления движению шариков малого диаметра в жидкости разработана Стоксом . Он нашел, что шарик радиусом г, движущийся с постоянной скоростью (стационарно) и, испытывает в вязкой жидкости сопротивление
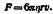
Если движение совершается под влиянием силы тяжести, то сила, приложенная к шарику, равна:
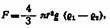
где g — ускорение силы тяжести, g = 981 см/сек2,
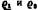 — соответственно плотности шарика и жидкости. подставляя в формулу Стокса, получим: — соответственно плотности шарика и жидкости. подставляя в формулу Стокса, получим:
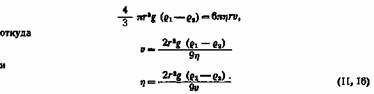
Если движение шарика обусловлено центробежной силой, возникающей, например, при центрифугировании, то
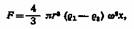
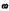 — угловая скорость; — угловая скорость;
х — расстояние частицы от центра вращения.
Приравнивая приложенную силу к силе сопротивления движению частицы, получим
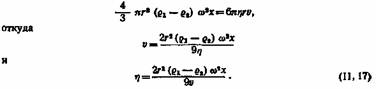
Закон сопротивления Стокса соблюдается при следующих условиях: 1) шарики обладают правильной сферической формой, гладки и не деформируются: 2) шарики двигаются на достаточном расстоянии от дна и стенок сосуда, в противном случае последние оказывают тормозящее действие; 3) количество шариков настолько мало, что их взаимодействие исключено; практически при вискозиметрии наблюдают движение одного шарика; 4) жидкость гомогенна (однородна) или неоднородности (например, частицы коллоидной взвеси) значительно меньше двигающихся шариков; 5) в жидкости нет никаких посторонних движений (конвекционных токов, течения жидкости, движения пузырьков газа и т. д.); 6) между шариком и жидкостью отсутствует скольжение; 7) скорость движения шариков настолько мала, что вокруг них устанавливается ламинарное течение жидкости; по этой же причине радиус шарика должен быть мал.
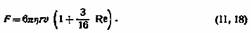
Уравнение Озеена при малых скоростях незначительно отличается от уравнения Стокса. Так, до Re < 1 разница не превышает 1%. С увеличением скорости роль поправки возрастает. Уравнение (II, 18) применимо с достаточным приближением до Re = 10. Существуют формулы и для более высоких скоростей движения, например, соотношение Аллена:

Оно пригодно в интервале от^е=10до^е^ 200.
Однако эти уравнения имеют частное значение и не всегда достаточно обоснованы. Вязкость с помощью падающих шариков измеряют при Re <Ю, а, как правило, при Re < 0,2 — 0,5, когда применимо уравнение Стокса.
Были предложены многочисленные поправки для учета других условий применимости уравнения Стокса, которые на практике часто трудно выполнимы. Так, Ладенбург ввел поправку на влияние стенок сосуда, его формула для вычисления вязкости имеет вид
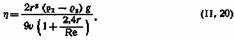
Если движутся шарики эмульсии, необходимо учитывать свойства не только внешней, но и внутренней фазы. Рибчинский и Гадамар ввели поправку на влияние вязкости жидкости шарика эмульсии. Формула Стокса с их поправкой имеет такой вид:
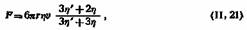
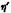 — вязкость капель эмульсии (внутренней фазы). — вязкость капель эмульсии (внутренней фазы).
А. Н. Фрумкин и В. Г. Левич нашли, что поправка Рибчинского и Гадамара недостаточна, так как не учитывает поляризации, возникающей на границе капли, и других электрохимических эффектов. Они вывели следующую формулу скорости движения капли эмульсии в жидкой дисперсионной среде под влиянием силы тяжести:
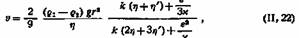
где £ — величина заряда капелек эмульсий; ж — электропроводность раствора;
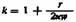 , где w— величина, зависящая от природы электрохимического , где w— величина, зависящая от природы электрохимического
процесса.
Формула Стокса позволяет не только вычислить вязкость из скорости движения и размера шариков, но и найти последнюю из скорости и вязкости. На этом основан седиментационный анализ размеров частиц суспензий и коллоидов .
М. М. Кусаков и А. Н. Кислинский показали, что при высокой вязкости формулой Стокса с достаточной для практики точностью можно пользоваться при измерении падения шариков в среде с переменной вязкостью . Это заключение нашло применение для измерения вязкости при низких температурах (см. главу III).
Единицы измерения и способы выражения вязкости
Коэфициент вязкости или динамическая вязкость в физико-химической литературе обозначается принятой в этой книге буквой rjt в гидродинамической литературе — буквой /.

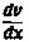 равными единице, то из уравнения Ньютона имеем равными единице, то из уравнения Ньютона имеем
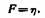
Единица вязкости в системе CGS равна силе, способной поддерживать между двумя параллельными плоскостями, имеющими площадь 1 см2 и находящимися друг от друга на расстоянии 1 см, градиент скорости, равный 1 сек."1. Она называется пуазом. 1 пуаз = 1 г/см сек.
Вязкость, равная 1 пуазу, — довольно большая величина, поэтому часто •пользуются сотой частью пуаза—сантипуазом (вязкость воды при 20° очень близка к 1 сантипуазу). Динамическую вязкость газов обычно выражают в тысячных долях пуаза, т. е. в миллипуазах.
Иногда в технической литературе вместо пуаза пользуются единицей динамической вязкости в системе MTS, названной мириапуазом (обозначение Мп). 1 мириапуаз — 1 т/м сек = 1 стен сек/м = 10000 пуаз.
В отдельных редких случаях выражают динамическую вязкость в системе MKS (табл. 2).
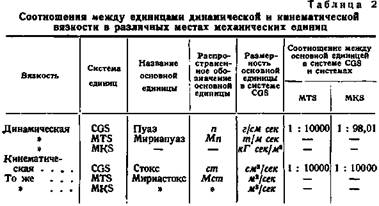
В выражение для числа Рейнольдса входят две величины, связанные с природой жидкости; вязкость и плотность. Первая характеризует внутреннее трение, вторая — массу единицы объема. Их отношение носит название кинематической вязкости и обозначается буквой v:
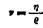
Эта величина получила широкое распространение в нефтяной вискозиметрии. Помимо своего теоретического значения она удобна благодаря простым формулам, связывающим ее с техническими единицами вязкости.
Размерность динамической вязкости ML~iT,~~l, размерность плотности М1Г следовательно, размерность кинематической вязкости LiT~i- Единица кинематической вязкости в системе CGS носит название стоке. 1 стоке равен 1 см2/сек. Чаще пользуются сотой долей стокса — сантистоксом.
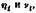 например, т)го = 0,01 пуаза. например, т)го = 0,01 пуаза.
Стандартных обозначений для пуаза и стокса нет. Нередко сокращенно пишут: пуаз — п, сантипуаз — сп, стоке—cm, сантистоск — ест,
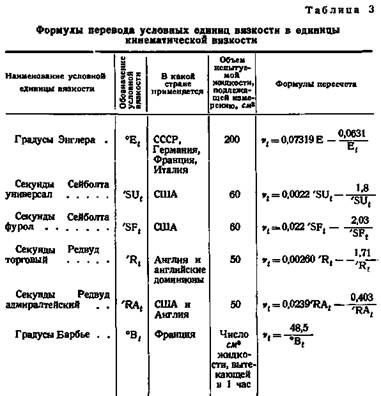
Часто в технике вязкость условно оценивается временем протекания определенного объема жидкости через трубу в стандартных условиях или количеством жидкости, протекающей за определенное время в этих же условиях. Из формулы Пуазейля следует, что вязкость прямо пропорциональна первой величине и обратно пропорциональна второй. Для таких измерений разработаны многочисленные приборы. Из них в нефтяной практике находят применение вискозиметры Энглера, Сейболта (в двух модификациях: универсал и фурол), Редвуда (в двух модификациях: торговый и адмиралтейский) и Барбье. Все эти приборы выражают вязкость в условных единицах, носящих название градусов (для вискозиметров Энглера и Барбье) или секунд (для вискозиметров Сейболта и Рудвуда).
Условные единицы неудобны, и применение их нецелесообразно, так как отрывает технические измерения от научно-обоснованных. Вязкость, выраженная в технических единицах, не является физической характеристикой жидкости. К тому же приборы, с помощью которых они определяются, не всегда удовлетворяют требованиям точной вискозиметрии и не позволяют охватывать достаточно широкий диапазон вязкостей. В Советском Союзе технические методы вискозиметрии нефтепродуктов и соответственно условные технические единицы почти полностью вытеснены единицами кинематической или динамической вязкости. Однако условные единицы пока еще сохраняются для отдельных видов нефтепродуктов. В Западной Европе и США устаревшие технические единицы широко распространены и часто встречаются в зарубежной литературе.
Связь между динамической вязкостью, плотностью и градусами Энглера выражается формулой
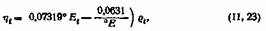
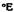 — градусы Энглера. — градусы Энглера.
Формулы для перевода условных единиц вязкости в единицы кинематической вязкости сведены в табл. 3. В ГОСТ 33-46 приведены таблицы для перевода кинематической вязкости в условную вязкость по Энглеру и обратно.
На основе уравнений Пуазейля, Стокса и формулы (II, 14) вязкость может быть вычислена по скорости течения и размерам прибора. Таким путем измеряют абсолютную вязкость. Однако точные измерения размеров вискозиметра довольно сложны, поэтому обычно сравнивают скорость течения (например, времени протекания через капилляр) исследуемой жидкости и жидкости, вязкость которой известна. При течении через капилляр вычисление производят с помощью формулы (II, б). Отношение одной вязкости к другой дает относительную вязкость:
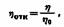
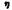 — вязкость исследуемой жидкости; — вязкость исследуемой жидкости;
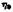 — вязкость известной жидкости. — вязкость известной жидкости.
Относительной вязкостью удобно пользоваться при сравнении вязкости растворов (в качестве щ принимают вязкость растворителя), для оценки влияния давления (щ вязкость при атмосферном давлении) и температуры на вязкость жидкостей и при других физико-химических исследованиях.
Терминами абсолютная и относительная вязкость часто пользуются в близком, но несколько другом смысле, чем изложено выше. Абсолютной называют вязкость, которую можно выразить в абсолютных единицах (динамическую и кинематическую), а относительной — вязкость, выраженную в условных или относительных единицах.
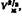 где VM — молекулярный объем. где VM — молекулярный объем.
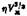 равна произведению молекулярной поверхности на силу, необходимую для поддержания градиента скорости течения жидкости, равного единице. Величину rjV . V lz = qV иногда называют молекулярной работой вязкости. равна произведению молекулярной поверхности на силу, необходимую для поддержания градиента скорости течения жидкости, равного единице. Величину rjV . V lz = qV иногда называют молекулярной работой вязкости.

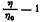 к концентрации раствора — удельной приведенной вязкости. к концентрации раствора — удельной приведенной вязкости.
В нефтяной литературе не всегда достаточно отчетливо различают относительную и удельную вязкость. Между тем они не только отличаются по величине (на единицу), но, как было показано нами совместно с Н. Г. Пучковым , функциональная зависимость этих двух выражений вязкости от концентрации растворов и температуры может быть существенно различной.
Предел, к которому стремится удельная приведенная вязкость растворов высокополимеров, при приближении концентрации к нулю некоторыми авторами не совсем удачно назван эффективной вязкостью или истинной вязкостью. Наконец, отношение натурального логарифма относительной вязкости к концентрации иногда называют логарифмической вязкостью.
Выражения вязкости, принятые в учении о высокомолекулярных соединениях, вводились в течение последних 15—20 лет, и пока еще, к сожалению, не существует общепринятой терминологии и обозначений. Так, например, С. М. Липатов , А. В. Думанский и др. обозначают удельную вязкость r)s. М. П. Воларович, В. Б. Маргаритов и др. пользуются обозначением д, а В. В. Коршак и С. Р. Рафиков и Б. А. Догадкин
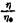 — 1 специфической вязкостью с обозначением ее через у . Последним обозначением также пользуется Штаудингер. — 1 специфической вязкостью с обозначением ее через у . Последним обозначением также пользуется Штаудингер.
В общем удачная унификация терминологии и обозначений была недавно предложена Г. Л. Слонимским, С. С. Воюцким и Ю. А. Марголиной (23).
Вызывает лишь сомнение одинаковый термин для
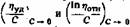 характер функциональной зависимости у них разный, и если сохранить последний способ выражения вязкости, то его следует называть иначе, например, логарифмическая приведенная относительная вязкость. характер функциональной зависимости у них разный, и если сохранить последний способ выражения вязкости, то его следует называть иначе, например, логарифмическая приведенная относительная вязкость.
Сводка терминов и способов обозначений вязкости, принятых в литературе, дана в табл. 4.
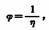
 — текучесть. — текучесть.
Единицы текучести обратны единицам вязкости. Величина, обратная пуазу, носит название ре (от греческого get — течь). В системе CGS 1 ре = = 1 см сек/г = 1 см2/ дн сек. По аналогии с вязкостью введены относительная текучесть, удельная текучесть и т. д. В пользу применения текучести существуют и некоторые теоретические соображения, однако этот термин не вытеснил более привычный — вязкость.
|