Вязкость и пластичность нефтепродуктовЗависимость деформации от нагрузки. Реологические кривые консистенции. Аномалия вязкости
Особенности механических свойств аморфных и дисперсных
тел. Минеральные масла при низких температурах, высоковязкие мазуты, консистентные смазки, битумы и некоторые другие нефтепродукты являются аморфными телами или дисперсными системами. По механическим свойствам такие тела занимают промежуточное положение между жидкостями и твердыми телами. Зависимость деформации от нагрузки у них неодинакова при различных нагрузках, так, например, консистентные смазки некоторых марок под малыми нагрузками ведут себя как упругие твердые тела, а под большими — как жидкости. Их механические свойства зависят от времени действия деформирующих сил и скорости нагрузки. Примером могут служить высокоплавкие битумы, которые при малой скорости нагрузки деформируются как жидкости, а при больших скоростях —как хрупкие твердые тела. Некоторые кривые зависимости деформации от нагрузки представлены на фиг. 3.
Упомянутые особенности механических свойств не специфичны для аморфных и дисперсных тел. Они могут обнаруживаться и у реальных жидкостей и у твердых тел (см. фиг. 3), но если они наблюдаются у этих тел при больших нагрузках или в особых, иногда исключительных, состояниях, то для многих аморфных и дисперсных тел они присущи обычным деформациям. При изучении твердых и жидких тел часто можно не учитывать изменения их механических свойств с возрастанием величины нагрузки или времени ее действия. Для большинства аморфных и дисперсных тел роль этих факторов так велика, что ими нельзя пренебречь.
Учение о деформациях таких тел составляет предмет нового раздела физической механики, получившего название реологии.
Основы реологии были заложены классическими исследованиями Ф. Н. Шведова. На примере разбавленных золейжелатины он экспериментально показал, что жидкости могут обладать модулем упругости и периодом релаксации1. Таким образом, им впервые были описаны несовершенные жидкости, совмещающие в себе свойства жидкостей и твердых тел. Такие тела с равным основанием можно назвать несовершенными твердыми телами. В современной реологии существует два направления: одно стремится разработать законы деформации таких тел, исходя из законов течения жидкостей, другое —из законов деформации твердых тел.
Понятие о периоде релаксации было введено в науку Максвеллом. Рассматривая соотношение между относительной деформацией тела Ае и действующей на него внешней силой F, он пришел к следующему уравнению:

где Е — модуль Юнга; — время действия силы F; ц — вязкость.
Первое слагаемое правой части уравнения учитывает упругость тела,
второе — его вязкость. Отношениеимеет размерность времени и носит
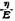
Из уравнения (I, 13) можно получить следующее соотношение:
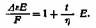
Подставляя время релаксации Т, имеем:

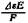 больше единицы даже при малом больше единицы даже при малом
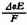 близко к единице, т. е. де- близко к единице, т. е. де-
формация будет упругой.
Впрочем и в этом случае деформация может быть необратимой, если сила F действует продолжительное время (t велико). Известно свойство многих твердых упругих тел медленно деформироваться под длительным действием нагрузок. Это свойство получило название ползучести или криппа.
Графики зависимости деформации от нагрузки. Реологические тела. Для характеристики деформации в реологии широко применяются графики, изображающие зависимость деформации от нагрузки, в частности, графики зависимости градиента скорости течения 5 от напряжения сдвига т. Такие кривые носят название реологических кривых консистенции.
Понятие консистенция не имеет вполне четкого физического смысла. В реологии оно означает свойство материалов сопротивляться необратимым изменениям формы и измеряется отношением величины деформации (в частности, расхода жидкости) к напряжению. Неопределенность этого понятия зависит от различных видов зависимости S от т.
Часто для изображения кривой консистенции вместо градиента скорости пользуются расходом Q в капиллярном вискозиметре или числом оборотов цилиндра в ротационном вискозиметре Л. Вид функций S = /(т), Q = f(p) и N = /(G) (р —разность давлений в капиллярном вискозиметре; G—вес груза, вращающего цилиндр в ротационном приборе) одинаков, но первая существенно отличается от остальных тем, что она выражает зависимость диференциальной величины, в то время как Q и N являются интегральными величинами.
 откуда видно, что уменьшению угла а соответствует увеличение вязкости. откуда видно, что уменьшению угла а соответствует увеличение вязкости.
Кривая 6 отвечает телу, обладающему свойствами, противоположными свойствам ньютоновской жидкости. Она характеризует идеально хрупкое твердое тело. До некоторого предела напряжения деформации нет (здесь не градиент скорости, а относительная деформация), но после достижения критической величины тело разрушается и деформация его уже не зависит от напряжения.
Все остальные кривые консистенции укладываются между этими двумя крайними типами.

Кривая 2 характеризует реологическое тело, в котором деформация начинается лишь после того, как напряжение достигнет некоторого предела, получившего название предельного напряжения сдвига 0. Выше предельного напряжения сдвига величина деформации пропорциональна напряжению, как и у ньютоновской жидкости. В литературе это тело часто называют бингамовым телом. М. П. Вола-рович развил теорию деформации этого тела и приложил ее ко многим объектам, поэтому правильнее называть его телом Бингама-Воларовича.
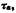 то может оказаться, что вязкость тела / больше, чем вязкость тела 2 (угол аг < угла а2), а при напряжении г в вязкость тела 2 больше вязкости тела / то может оказаться, что вязкость тела / больше, чем вязкость тела 2 (угол аг < угла а2), а при напряжении г в вязкость тела 2 больше вязкости тела /

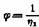 — текучесть; в — предельное напряжение сдвига. — текучесть; в — предельное напряжение сдвига.
Это уравнение иногда записывают в следующей форме:
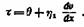
г]х в отличие от ньютоновской вязкости называется пластической вязкостью или бингамовской вязкостью.

Исследуя в капиллярных вискозиметрах расход суспензий глин в воде, красочных пигментов в маслах и некоторых других объектов, Бинтам нашел, что уравнение (I, 15) с достаточным приближением описывает их деформацию. Аналогичные результаты получены М. П. Воларовичем в ротационном вискозиметре.
Фиг. 10. Схема кривой, выражающая аномалию вязкости.
Одновременно этими и многими другими авторами были изучены тела, не подчиняющиеся такому простому уравнению. Так течение значительного числа коллоидных растворов и суспензий начинается при весьма малых напряжениях, но градиент скорости непропорционален
напряжению (кривая J, фиг. 8). Такие тела являются жидкостями, так как у них нет предела текучести, но при напряжениях выше Tj (фиг. 8, 3) они ведут себя как пластичные тела, и если ограничиться исследованиями выше этой области, то их можно принять за тела Бингама-Воларовича. Следует, однако, отметить, что исследовать течение при малых напряжениях затруднительно, поэтому во многих случаях нет полной уверенности в том, что кривая консистенции проходит через начало координат. Эти тела называются псевдопластичными.
Псевдопластичные тела являются не ньютоновскими жидкостями. У этих тел при увеличении градиента скорости течения вязкость уменьшается (отрезок кривой фиг. 10 между SminH Si) до некоторого предела. Когда этот предел достигнут, вязкость становится постоянной до наступления турбулентности при St, когда она опять начинает возрастать. Снижение вязкости с повышением градиента скорости течения противоречит закону Ньютона и носит название аномалии вязкости.
Кривые, подобные изображенной на фиг. 10, были получены в разнообразных вискозиметрах. Для капиллярного вискозиметра признаком псевдопластичности служит снижение вязкости с повышением разности давлений, обусловливающей протекание жидкости. В ротационном вискозиметре вязкость уменьшется с увеличением груза, вращающего цилиндр вискозиметра.
Величина вязкости псевдопластичных тел зависит не только от разности давлений или груза, но и от размеров прибора1, а часто также от предварительных механических и термических воздействий на исследуемое тело. Было показано, что на вязкость рассматриваемых тел влияет способ получения напряжения, при котором измеряется вязкость, а именно путем наложения или снятия нагрузки.
Таким образом вязкость псевдопластичных тел зависит не только от свойств тела, но и от условий опыта. Ее называют кажущейся или эффективной вязкостью. Мы будем обозначать ее ?7а. С возрастанием напряжения г?а падает от ^тахДо ymin (фиг. 10). Режим течения, при котором кажущаяся вязкость остается постоянной при различных напряжениях, носиг название псевд о ламинарного течения. г}тщ иногда называют остаточной вязкостью. Необходимо отметить, однако, что установление псевдоламинарного режима еще не означает, что 7jmin действительно является наименьшей вязкостью, так как может оказаться, что в других приборах или при повторных нагрузках будет достигнуто более низкое значение вязкости.
Очень интересен вопрос о характере течения при градиентах скорости между S0 и Smin (фиг. 10). По мнению Филиппова и Рейнера , в этой области может иметь место ньютоновская вязкость. Область постоянной вязкости при весьма малых градиентах скорости получила название рейнеровской или филиппов-ской области. Существование этой области было показано на примере вязких минеральных масел при низких температурах. Все же можно думать, что линейный участок кривой щ = f(S) для S < 5ш1пПолучается не у всех псевдопластичных тел, а главное, не во всех опытах.
Полная реологическая кривая консистенции псевдопластичных тел изображена на фиг. 8 (кривая 4). Она называется ост-вальдовской реологической кривой. Весь отрезок а — область аномалии вязкости, отрезок 6 — псевдоламинарная область и отрезок в—область турбулентного режима. Оствальдовская кривая является не единственным видом реологической кривой псевдопластичного тела. Так, у некоторых золей продолжение отрезка б в сторону оси абсцисс не проходит через начало координат. Наиболее простая не ньютоновская жидкость получила название максвелловской жидкости. Ее сопротивление течению складывается из внутреннего трения и упругости. Она может служить примером упруго-вязкой жидкости. Для описания течения такой жидкости необходимо знать ее вязкость и модуль упругости.
Теория деформации псевдопластичных тел мало разработана. Эйзен-1ПИТЦ построил теорию аномалии вязкости, основанную на предположении, что при малых напряжениях каждый элементарный объем жидкости не успевает релаксировать во время деформации, т. е. перейти от напряженного состояния в деформированное со скоростью, соответствующей скорости течения. В области высоких напряжений релаксация протекает быстрее и поспевает за скоростью течения. Сохранение напряженного состояния в жидкости означает малую деформацию по отношению к приложенному напряжению, что на опыте будет регистрироваться как высокая вязкость. Вследствие уменьшения потери напряжения при высоких значениях последнего т)а падает с ростом т. Он вывел следующее уравнение:

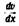 —градиент скорости; т — напряжение; у— модуль упругости. —градиент скорости; т — напряжение; у— модуль упругости.
Из теории вытекает, что с повышением напряжения сдвига вязкость должна неограниченно падать. Это противоречит опыту, вследствие чего уравнение Эйзеншитца не нашло практического применения, хотя идеи, использованные при его выводе, представляют интерес.
Филиппов в своей теории аномальной вязкости исправил уравнение . Согласно Филиппову
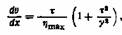
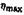 — вязкость в филипповской области. — вязкость в филипповской области.
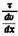 является кажущейся вязкостью. является кажущейся вязкостью.
Обозначая ее через а и подставляя в уравнение, получим
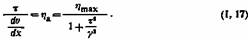
Рассматривая tja как сумму аномального и истинно вязкого компонентов, Филиппов приводит свое уравнение к следующему виду:

Проверка этого уравнения показала, что оно применимо для некоторых коллоидных растворов. В. П. Варенцов пытался использовать его для характеристики течения консистентных смазок, но А. А. Константинов обнаружил, что оно непригодно для этих целей.
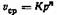 и уравнение, полученное автором совместно с Т. А. Мечков- и уравнение, полученное автором совместно с Т. А. Мечков-
ской : lgj/a = Kj—Ка lg Re (Кг и Ка не зависят от геометрических размеров капилляра вискозиметра). Однако первое из этих уравнений дает неудовлетворительные результаты, так как скорость течения vcp зависит не
только от давления, но и от размеров капилляра, а второе применимо для ограниченного круга дисперсных систем и в специальных условиях.
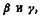 кривая 4, фиг. 8). Это отношение кривая 4, фиг. 8). Это отношение
имеет определенный физический смысл для тела, обладающего оствальдовской кривой, рейнеровской областью и в том случае, когда rain является остаточной вязкостью. Перечисленные условия не всегда соблюдаются, и проверка их представляет значительные, иногда непреодолимые, трудности. Тем не менее отношениев определенном интервале градиентов скорости, при
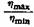 что измерения вязкости проводятся в одном приборе, представляет значительный интерес для качественной оценки аномалии вязкости. Для этой же цели может оказаться целесообразным воспользоваться градиентом падения вязкости что измерения вязкости проводятся в одном приборе, представляет значительный интерес для качественной оценки аномалии вязкости. Для этой же цели может оказаться целесообразным воспользоваться градиентом падения вязкости
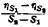 ниже предела текучести пластичное тело не деформируется. Между тем у реальных тел это не соответствует действительности. В наиболее простом случае при напряжении, меньшем 0St тело деформируется по закону Гука. Такие тела будут упруго-пластичными. Их механические свойства ниже предела текучести оцениваются модулем упругости. Таким образом, для полного описания наиболее простого упруго-пластичного тела необходимы по крайней мере три параметра: модуль упругости, вязкость и предельное напряжение сдвига, определяющее переход от упругой деформации к вязкому течению. ниже предела текучести пластичное тело не деформируется. Между тем у реальных тел это не соответствует действительности. В наиболее простом случае при напряжении, меньшем 0St тело деформируется по закону Гука. Такие тела будут упруго-пластичными. Их механические свойства ниже предела текучести оцениваются модулем упругости. Таким образом, для полного описания наиболее простого упруго-пластичного тела необходимы по крайней мере три параметра: модуль упругости, вязкость и предельное напряжение сдвига, определяющее переход от упругой деформации к вязкому течению.
Аномалия вязкости может иметь место не только у жидкости, но и у пластичного тела (кривая 5, фиг.8). Одно из тел этого класса получило название тела Шведова. Оно отличается от тела Бингама-Воларовича тем, что обладает двумя упругостями: одной выше предельного напряжения сдвига, т. е. при течении, и второй ниже этой точки.
У таких тел существует два предела текучести. Первый, отвечающий напряжению, при котором начинается течение, назван статическим предельным напряжением сдвига 6S. Второй предел текучести обнаруживается подобно пределу текучести псевдопластичного тела путем экстраполяции прямолинейного участка кривой, отвечающего пластической вязкости, до пересечения с осью абсцисс. Напряжение, соответствующее отсеченному отрезку, получило название динамического предельного напряжения сдвига и обозначается да (кривая 5, фиг. 8). У тела Бингама-Вола-ровича 9S и О совпадают, а у псевдопластичного тела есть только Od.
Необходимо отметить существенное отличие всякого реального тела от реологического, заключающееся в том, что оно может деформироваться по различным законам в зависимости от условий
Реологические тела собственно соответствуют не реальным телам, а их состояниям и описывают реологические явления.
Для практических целей обычно нет необходимости в полном описании деформации тела. Например, если производится прокачивание высоковязкого мазута, то его упругость ниже предела текучести не представляет интереса, а если оценивается несущая способность битума, то его вязкость выше предела текучести не измеряется. Это очень упрощает частное описание реальных тел и позволяет для отдельных случаев применения
нефтепродуктов ограничиваться одним-двумя параметрами. Следует лишь иметь в виду, что другие виды применения могут потребовать и другие параметры. Например, когда оценивается вяжущая способность битума, имеет значение не модуль упругой деформации, а параметры, характеризующие течение выше предельного напряжения сдвига.
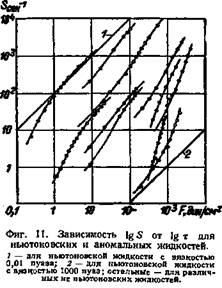
Для решения некоторых задач реологии удобно пользоваться графиком зависимости gS от lg т. Б. А. Догадкин с успехом применил этот метод для анализа деформации растворов каучука в бензоле. Для ньютоновских жидкостей зависимость gS от lg r линейна. Угол наклона прямой равен 45°. Возрастание вязкости смещает прямые в правую часть графика (фиг. 11). Для псевдопластичных и других не ньютоновских жидкостей зависимость gS от lg т нелинейна и наклоны отдельных отрезков кривой по отношению к оси абсцисс отличны от 45°.
Разработан также принцип количественной характеристики реологических явлений, основанный на оценке превращений энергии при деформации. В треугольных координатах (фиг. 12) в
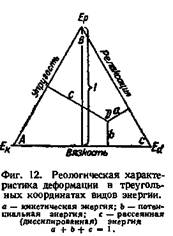
качестве одной оси выбрана вязкость, второй — упругость, третьей —релаксация. В точке А вся работа, совершаемая внешними силами, переходит в кинетическую энергию; в точке В в потенциальную энергию, что соответствует идеально упругому телу; точка С соответствует нормальной вязкой жидкости в условиях ламинарного потока. Гуково тело в рассматриваемых координатах представлено точкой на оси ЛЯ, ньютоновская жидкость — точкой на оси АС.
Все деформации характеризуются точками внутри треугольника ABC. Для деформации D длина отрезка а отвечает величине кинетической энергии, длина отрезка Ь —потенциальной энергии, длина отрезка с —диссипированной энергии.
Энергетическое описание деформации представляет значительный теоретический интерес, но пока оно еще мало применяется в реологии нефтепродуктов. Следует ожидать, что его значение будет возрастать при дальнейшей разработке учения о вязкости я пластичности.
|