Влияние концентрации и объема растворенного вещества на вязкость раствора

При количественной трактовке зависимости вязкости растворов от концентрации различают разбавленные и концентрированные растворы. Для первых существуют теоретически обоснованные закономерности, связывающие вязкость растворов с концентрацией и физико-химическими свойствами растворенного вещества. Для вычисления вязкости концентрированных растворов пользуются преимущественно эмпирическими уравнениями, рассмотренными выше.

Закон вязкости разбавленных растворов установлен А. Эйнштейном , который показал, что вязкость раствора или взвеси шарообразных частиц зависит от отношения объема растворенного вещества v к объему раствора V и не зависит от размера частиц растворенного вещества:

;

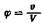а—константа, равная для шарообразных частиц 2,5.

При выводе этого уравнения Эйнштейн исходил из следующих предпосылок: 1) молекулы растворенного вещества значительно больше молекул растворителя и очень невелики по сравнению с линейными размерами вискозиметра; 2) молекулы растворенного вещества не деформируются при течении и полностью удерживают растворитель; 3) концентрация раствора настолько незначительна, что частицы или молекулы не взаимодействуют между собой;

частицы распределены в растворе беспорядочно и равномерно;

молекулы или частицы растворенного вещества имеют достаточно правильную шарообразную форму; 6) течение раствора стационарно и происходит настолько медленно, что число Рей-нольдса меньше единицы. Инерционные силы могут не учитываться.

Только при соблюдении этих условий полностью справедлив закон вязкости Эйнштейна.

Если выразить концентрацию раствора в г/л, удельный вес раствора обозначить через q и ввести удельную вязкость

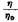— 1, то уравнение (IV, 34) можно переписать в виде

Если нет сольватации, то для растворенных частиц независимо от их размера К = 0,0025. Постоянство этой величины было установлено с достаточным приближением для ряда коллоидных и истинных растворов (гуммигут, латекс каучука, гликоген), что послужило экспериментальным подтверждением уравнения Эйнштейна.

Растворы и суспензии, содержащие вытянутые и другие нешарообразные частицы, не подчиняются закону Эйнштейна. В частности, ему не подчиняются растворы парафиновых углеводородов.

На основании многочисленных измерений Штаудингер пришел к заключению, что вязкость растворов нитевидных, линейных молекул может быть выражена уравнением

где с —концентрация; М —молекулярный вес; К —постоянная величина. Величина К зависит от типа соединения, но внутри гомологического ряда она должна быть постоянной. Значения К для отдельных классов соединений приведены в табл. 25.

Штаудингер принимает, что действующий объем растворенной нитеобразной молекулы вследствие вращения последней больше ее истинного объема и возрастает пропорционально квадрату длины молекулы. По С. М. Липатову сферу действия такой молекулы можно представить в виде объема шара, диаметр которого равен длине молекулы. Эйзеншитц дал теоретическое обоснование зависимости вязкости раствора нитеобразных молекул от квадрата их длины.

Таким образом, удельная вязкость представляет собой функцию строения отдельного члена цепи и числа структурных единиц, входящих в состав молекул. У нормального парафинового углеводорода она аддитивно складывается из инкрементов отдельных групп СН2, составляющих молекулу. Для низших членов многих гомологических рядов эта закономерность хорошо соблюдается. Уравнение (IV, 35) не имеет универсального значения. В последнее время Штаудингер и другие авторы обнаружили поли-мергомологические рзды, внутри которых значение величины К меняется в два и большее число раз (полиметилметакрилаты, поливинилхлориды и др.). Значительные отклонения от закона Штаудингера наблюдались у крупных молекул с числом членов цепи больше 500—1000. По мнению большинства авторов, эти отклонения объясняются деформацией длинных молекул. Изгибание длинных молекулярных цепей было обнаружено рентгенографическими и другими методами. При скручивании молекул в растворе увеличивается количество связанного (иммобилизованного) ими растворителя, что также отражается на действующем объеме.

Измерения Мейера показали, что и у молекул с очень короткими цепями величина К несколько изменяется, что, пови-димому, объясняется влиянием концевых групп. По мере удлинения цепи величина К становится более постоянной.

Исходя из тех или иных представлений о причинах отклонений от закона Штаудингера, были предложены поправки к его уравнению. Принимая изогнутую форму цепеобразных молекул, приводящую к повышенной иммобилизации растворителя и соответственно к более быстрому нарастанию удельной вязкости с повышением молекулярного веса, Марк ввел добавочный член в это уравнение.

где а—вторая постоянная величина, близкая к 0,2. Фордис, Ловел и др. ввели добавочный член Д, связанный, по их мнению, с сольватацией

Крэмер нашел линейную зависимость между внутренней, или истинной, вязкостью и молекулярным весом.

Необходимо отметить, что на удельную вязкость влияет не только природа растворенного вещества, но в меньшей степени и свойства растворителя. Данные, приведенные в табл. 25, показывают, что прежде всего имеет значение полярность растворителя. У растворителей с одинаковой полярностью заметную роль играет их вязкость . Для растворов, содержащих удлиненные частицы, наряду с эмпирическими формулами типа уравнения Штаудингера были разработаны теоретические уравнения, основанные на гидродинамических предпосылках. Так,Кун пришел к уравнению следующего вида

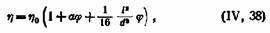
где I —длина частиц; d —толщина частиц; а —константа, равная 2,5.

Как легко видеть, уравнение (IV, 38) отличается от уравнения Эйнштейна членом, характеризующим степень асимметрии частицы.

Эйзеншиц математически более обоснованным способом получил уравнение, отличающееся от уравнения Куна численным значением коэфициента этого члена (1/30 вместо Vie)

Для растворов длинных палочкообразных частиц Бургерс вывел следующее уравнение:

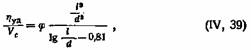
где 9?—ориентационный фактор, зависящий от броуновского движения. При интенсивном броуновском движении 9?=7i5

Практическое значение уравнения Штаудингера заключается в том, что оно позволяет вычислить молекулярный вес растворенных веществ по вискозиметрическим данным. Как видно из вышеизложенного, им можно пользоваться в ограниченных пределах. Для соединений с молекулярным весом, превышающим несколько десятков тысяч, оно вовсе непригодно. Величина эмпирической постоянной К должна тщательно определяться не только для выбранного типа соединения, но и для выбранного растворителя и диапазона молекулярных весов. При пользовании значениями /С, приведенными в литературе, следует обращать внимание на число членов молекулярной цепи, для которой оно определялось. Детальное описание факторов, влияющих на величину /С, дано в монографии В. В. Коршака и С. Р. Рафикова .

С помощью уравнения Эйзеншица, Куна и Бургерса, исходя из вискозиметрических данных, можно вычислить отношение длины частиц к их толщине, т. е. определить форму частиц. Следует иметь в виду, что первое и особенно второе уравнение дает несколько завышенное значение ljd. В работе А.Г. Пасынского приведена таблица для определения формы молекул, составленная на основании уравнений рассмотренного типа