Паровые турбины. Часть 2Расход пара через суживающиеся решетки
 для рабочей решеток. В ряде случаев удобно вместо (2.19) пользоваться приближенным уравнением эллипса (2.21), которое при соответствующем выборе масштаба заменяется уравнением дуги окружности. для рабочей решеток. В ряде случаев удобно вместо (2.19) пользоваться приближенным уравнением эллипса (2.21), которое при соответствующем выборе масштаба заменяется уравнением дуги окружности.
 перед, так и давления р1 за ней. перед, так и давления р1 за ней.
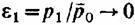 , то расход пара через решетку является , то расход пара через решетку является
критическим, т. е. наибольшим при данных параметрах перед решеткой (параметрах торможения) и согласно (2.18) и (2.36) равен
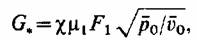 (7.1) (7.1)
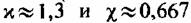
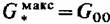 . Согласно (7.1) отношение . Согласно (7.1) отношение
критического расхода пара при начальном давлении
 , составит при неизменных коэффициенте расхода и показателе изоэнтропы (7.2) , составит при неизменных коэффициенте расхода и показателе изоэнтропы (7.2)
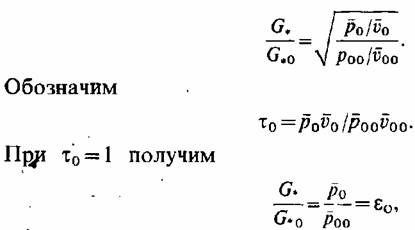 (7.3) (7.3)
 сохраняется сохраняется
постоянным.
В противном случае отношение удельных объемов будет зависеть не только от отношения давлений, но и от этого произведения (или от температуры пара), и относительный пропуск пара должен Определяться непосредственно по формуле (7.2), которая после преобразований приобретает вид
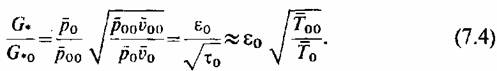
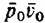 температурой температурой
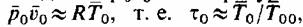
что допустимо при приближенных расчетах, а также для перегретого пара в определенной зоне параметров. Отметим, что на некоторых тепловых диаграммах проведены линии
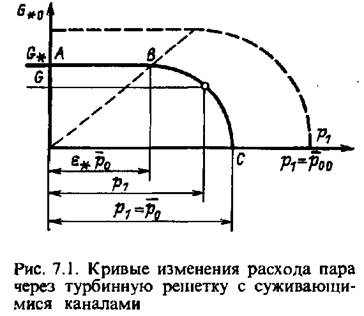
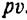
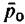 перед решеткой, менять давление за ней, то закон изменения расхода пара изобразится линией ЛВС (рис. 7.1), причем критическое отношение давлений для перегретого перед решеткой, менять давление за ней, то закон изменения расхода пара изобразится линией ЛВС (рис. 7.1), причем критическое отношение давлений для перегретого
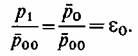
Таким образом, три основные точки А, В, С кривой рис. 7.1 (точка критического расхода пара, точка критического отношения давлений и точка нулевого расхода пара) при изменении давления перед решеткой сдвигаются пропорционально этому давлению.
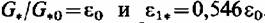
Воспользуемся формулой (2.21), представляющей связь между расходами и давлениями в докритической области,
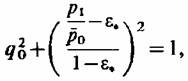 и, произведя простые преобразования, и, произведя простые преобразования,
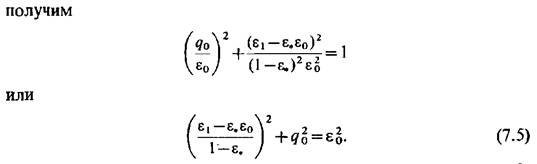
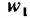 часто весьма значительна, следует пользоваться параметрами торможения. часто весьма значительна, следует пользоваться параметрами торможения.
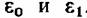
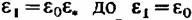
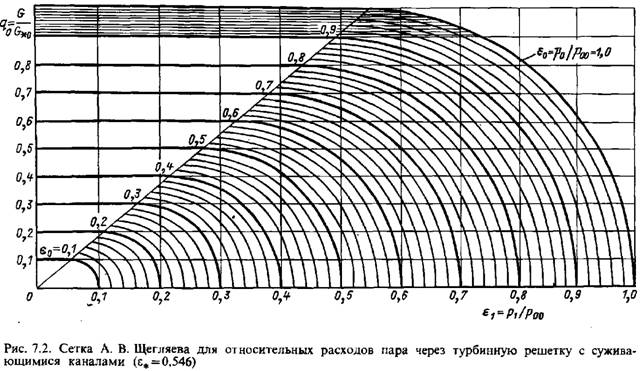
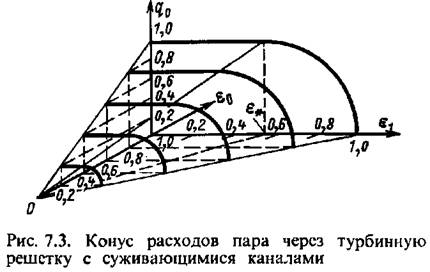
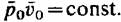 Касательный к поверхности конуса плоский треугольник соответствует области критических расходов пара. Касательный к поверхности конуса плоский треугольник соответствует области критических расходов пара.
Сетка расходов на рис. 7.2 была предложена А. В. Щегля-евым и носит его имя.
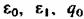 , определить третью. Так, например, если , определить третью. Так, например, если
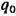 , найдем , найдем
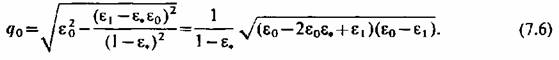
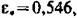 получим получим
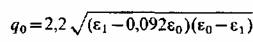
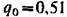
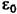 , получим , получим

что для перегретого пара может быть представлено в виде
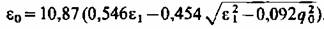
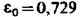 получим (с точностью до третьего знака), используя точную формулу, базирующуюся на зависимостях, представленных в приложении 2: получим (с точностью до третьего знака), используя точную формулу, базирующуюся на зависимостях, представленных в приложении 2:
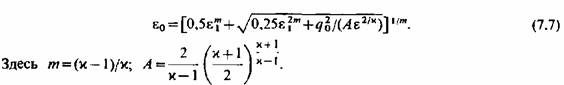
|