Паровые турбины. Часть 1Законы закрутки решеток
 задается косвенным пу- задается косвенным пу-
тем - через изменение по радиусу скоростей потока или их составляющих, или удельного расхода, или степени реактивности.
Рассмотрим некоторые законы закрутки из встречающихся в практике паротурбостроения.
 , получим , получим
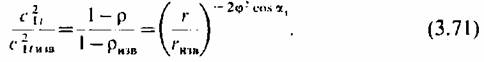
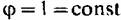
Использовав уравнение (3.65) в виде

 заменив соз а,= заменив соз а,=
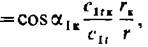 получим уравнение получим уравнение

Интегрируя его от гк до /-, получим выражение для скорости си:
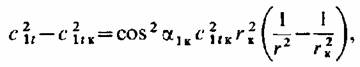
которое после простых преобразогний принимает вид
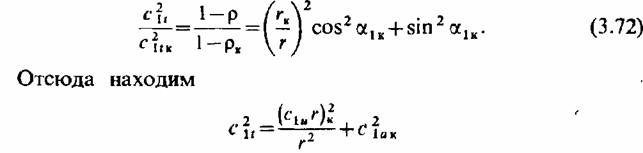
и, принимая во внимание, что

 , т. е. осевая со- , т. е. осевая со-
ставляющая скорости неизменна по радиусу.
 определяется выражением определяется выражением

Если и для потока за рабочей решеткой с2иг = соп81, то это означает, что удельная работа не меняется по высоте:
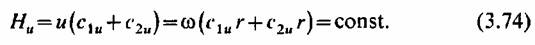
После преобразований уравнения радиального равновесия для состояния пара за рабочей решеткой, аналогичных выполненным выше, находим, что при коэффициенте скорости |/ = 1 осевая составляющая выходной скорости также остается неизменной по радиусу:

Для частного случая с2и = 0 получим

Для несжимаемой жидкости, т.е. при М,->0, условие с1а=соп§1 означает постоянство по радиусу удельного расхода, т. е. массового расхода пара на единицу площади. На рис. 3.17 сплошными линиями представлены результаты расчета для ступени с ^1//1 = ^2//2 = 3 в предположении несжимаемой жидкости.
3. Так называемый закон постоянства удельного расхода. Под удельным расходом в случае |Л = 1 и дозвуковых скоростей понимается величина:
для сопловой решетки
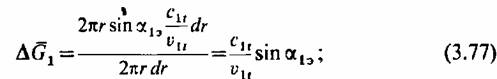
для рабочей решетки
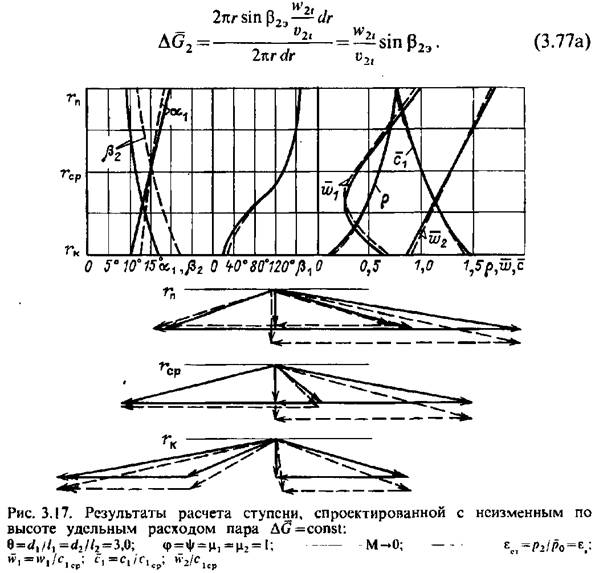
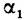 определяется в этом случае числами Мх. определяется в этом случае числами Мх.
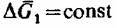 означает означает


 , т. е. меньше, чем по , т. е. меньше, чем по
 скорости становятся сверх- скорости становятся сверх-
 удельный расход удельный расход
подсчитывается по формуле
 I I
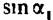 по радиусу для случаев М1-*0; Мг =0,6 по радиусу для случаев М1-*0; Мг =0,6
 означает, что при ф2/^г = 0 исрц2=1 означает, что при ф2/^г = 0 исрц2=1
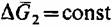 означает означает

 (см. рис. 3.8). Следовательно, и в этом случае угол (см. рис. 3.8). Следовательно, и в этом случае угол
Р2э к периферии падает.
 и большого и большого
теплоперепада: е=р2 /р0 = е+.
 , которые , которые
имеются в атласах профилей и для примера показаны на рис. 2.9. Как углы а1э, так и Р2э обычно с увеличением I несколько увеличиваются.
Если ступень с лопатками постоянного профиля рассчитать по упрощенному уравнению (3.70) в предположении
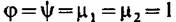 , то степень реактивности в ней по высоте будет меняться примерно так же, как и для ступеней, специально спроектированных с учетом пространственного изменения параметров. Однако детальный расчет по полным уравнениям с учетом искривления меридиональных линий тока и потерь при обтекании решеток и опыты, проведенные , то степень реактивности в ней по высоте будет меняться примерно так же, как и для ступеней, специально спроектированных с учетом пространственного изменения параметров. Однако детальный расчет по полным уравнениям с учетом искривления меридиональных линий тока и потерь при обтекании решеток и опыты, проведенные

с такими ступенями, показывают, что обычно реактивность от корня к периферии меняется существенно меньше, чем по упрощенному расчету. Это объясняется главным образом двумя причинами:
во-первых, сказывается существенное отклонение от цилиндрических и искривление поверхностей тока (рис. 3.19);
во-вторых, в сечениях рабочей решетки, удаленных от среднего, угол входа потока р! заметно отличается от расчетного угла (рис. 3.20), что приводит к повышенным потерям.
Анализ результатов расчетов нескольких видов ступеней и основных уравнений этого параграфа, более подробно выполненный в специальной литературе, позволяет сделать следующие выводы.
Расчет ступени по упрощенному уравнению (3.70) может быть использован как первое приближение. Полученное по нему изменение реактивности близко к истинному для ступени с цилиндрическими меридиональными обводами и постоянством по радиусу удельного расхода через обе решетки.
 слабо влияют на распределение но радиусу степени реактивности. Однако при расчете по полным уравнениям формы меридиональных обводов решеток и изменение профилей по радиусу могут существенно повлиять на распределение реактивности, в частности в ступенях с уменьшением к периферии угла а, уменьшается разница в реактивности у корня и периферии. слабо влияют на распределение но радиусу степени реактивности. Однако при расчете по полным уравнениям формы меридиональных обводов решеток и изменение профилей по радиусу могут существенно повлиять на распределение реактивности, в частности в ступенях с уменьшением к периферии угла а, уменьшается разница в реактивности у корня и периферии.
|