Схемы однослойных обмоток

Схемы и их классификация

После того как мы выяснили правила образования обмотки, перейдем к рассмотрению практического выполнения их схем.

Отметим, что схемы обмоток асинхронных и синхронных машин совершенно одинаковы.

Обозначим через Z — число пазов статора, 2р — число полюсов, т — число фаз.

Число пазов на фазную зону, или, как обычно называют, число пазов на полюс и фазу, будем обозначать через q.

В однослойных обмотках число пазов на полюс и фазу обычно бывает целым числом, хотя имеются однослойные обмотки и с дробным q. Ввиду того, что последние встречаются редко, мы их подробно рассматривать не будем. Двухслойные обмотки с дробным q будут рассмотрены ниже.

Так как в однослойных обмотках сторона катушки занимает весь паз, то число сторон катушек на фазной зоне будет равно числу пазов на фазную зону, т. е. q. Например, для обмотки, показанной на рис. 2-24, q = 2.

В целях облегчения производства, экономии меди на лобовых частях и уменьшения длины вылета обмотки остановились на двух основных видах ее изготовления.

Первый вид характеризуется тем, что все катушки катушечной группы имеют различную ширину и концентрически входят одна в другую. Такие обмотки обычно называют обмотками с концентрическими катушками (рис. 2-40, 6 и б).

Второй, вид изготовления характеризуется тем, что все катушки обмотки одинаковы (рис. 2-40, а и а , в ж в). Поэтому такие обмотки называют симметричными или шаблонными обмотками. Каждый из этих двух основных видов обмоток в свою очередь разделяется на типы, о которых будет сказано ниже.

Обмотки с концентрическими катушками

В однослойных обмотках на каждую пару полюсов и фазу приходится по одной катушечной группе. Таким образом, в общем случае обмотка имеет Зр катушечных групп.

Если р равно четному числу, то обмотка будет иметь четное число катушечных групп. В этих случаях можно поступить следующим

образом: лобовые части одной половины катушечных групп поместить в одной плоскости, а второй половины — в другой (рис. 2-41).

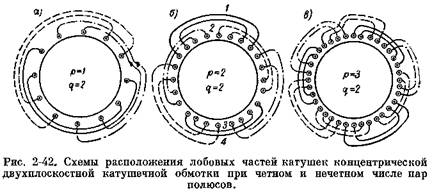
Если р равно нечетному числу, то обмотка будет иметь нечетное число катушечных групп. В этих случаях одна катушечная группа получается кривой или переходной. На рис. 2-42 изображены схемы концентрической обмотки при четном (рис. 2-42, б) и нечетном (рис. 2-42, а л в) числе пар полюсов с расположением лобовых частей в двух плоскостях. Обмотки такого типа носят название двухплоскостных концентрических катушечных обмоток.

На рис. 2-43 приведены торцовая (рис. 2-43, а) и развернутые (рис. 2-43, б) схемы обмотки с 2р = 4, 2 = 36, q — 3, соединение фаз — звездой. На рис. 2-43, б показана схема обмотки при а = 1, а на рис. 2-43, в — при а = р = 2.

Если лобовые части одной половины катушек каждой катушечной группы отогнуть в одну сторону, а второй половины в другую, то получим две полугруппы (рис. 2-45). Тогда число катушечных полугрупп в каждой фазе будет равно числу полюсов, и лобовые части их займут на торцовой поверхности статора всю окружность.

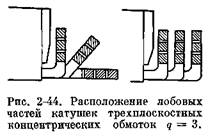
В этом случае лобовые части катушек одной фазы располагаются в одной плоскости, а лобовые части катушек трех фаз — в трех плоскостях (рис. 2-44). Такие обмотки носят название трех-плоскостных концентрических обмоток. Часто их называют концентрическими обмотками вразвалку, показывая этим, что катушки катушечной группы отгибаются в разные стороны. Полная схема такой обмотки изображена на рис. 2-45. Так как лобовые части каждой фазы располагаются в одном слое, то в этих обмотках удается избежать кривых катушек при нечетном числе пар полюсов р.

Характерной особенностью концентрических обмоток является то, что катушки имеют различную форму и длину. Это надо иметь в виду при образовании параллельных ветвей, так как нам необходимо не только равенство э. д . с параллельных ветвей, но и равенство активных и индуктивных сопротивлений ветвей. В противном случае при равных э. д. с. токи в ветвях могут получиться неравными.

Для того чтобы активное и индуктивное сопротивления ветвей (в двухплоскостных обмотках) были одинаковыми, необходимо,

чтобы в каждую параллельную ветвь вошло по одинаковому числу катушечных групп из обеих плоскостей. Обозначая число параллельных ветвей каждой фазы через а, получим, что число катушечных групп из каждой плоскости в параллельной ветви будет равно р/2а.

Поэтому только в том случае, когда р/2а равно целому числу, мы сможем получить обмотку с равными сопротивлениями. При а = 2 это возможно только при р = 4, 8,12 и т. д. Во всех остальных случаях сопротивления параллельных ветвей получаются не одинаковыми. Чтобы избежать этого (при четном числе пазов на полюс и фазу), можно образовывать параллельные ветви не из целых катушечных групп, а из полугрупп. Предположим, что р = 2 и q — 2 (рис. 2-42, б). Катушка 1 наиболее длинная, а катушка 3 наиболее короткая. Поэтому включая катушки 1 и 3 в одну параллельную ветвь и катушки 2 и 4 в другую, получим значительно меньшее расхождение в сопротивлениях ветвей.

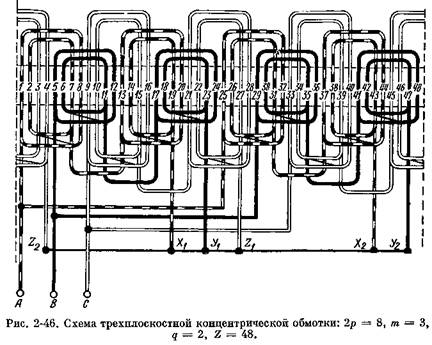
В трехплоскостных обмотках катушечные группы фазы лежат

в одной плоскости (рис. 2-46). Поэтому образование параллельных ветвей в них не встречает затруднений в смысле неравенства сопротивлений ветвей. Сопротивления же фаз получаются неодинаковыми

так как форма и размеры катушечных групп различны. Чтобы избежать этого, можно катушку, длинную с одной стороны

статора, сделать короткой с другой, что, конечно, усложняет производство.

Таким образом, двух- и трехплоскостные обмотки по существу являются обмотками несимметричными.