Кузнечно-штамповочное оборудованиеТермомеханический расчет паровоздушных молотов
Термомеханическая система тепловой машины
Для тепловых машин типично взаимное преобразование термической и механической энергии, поэтому эти машины можно считать термомеханическими или системами с двумя степенями свободы.
У большинства тепловых машин, в том числе у паровоздушных и газовых молотов, термомеханическая система в качестве поверхностей раздела содержит цилиндр и поршень, а в качестве рабочего тела - находящийся в цилиндре газ или водяной пар (далее пар). Подвижность поршня определяет механическую внешнюю степень свободы, а ввод (отвод) газом или паром теплоты (термическая работа) в систему (из системы) - термическую внешнюю степень свободы. В этом смысле газ или пар исполняет функции переносчика энергии, поэтому его часто называют энергоносителем.
Если энергоносителю (газу) придают идеальные свойства: 1) силы взаимодействия между молекулами газа отсутствуют, а сами молекулы - это материальные точки, не имеющие геометрического объема и 2) свойства идеального газа в любой точке термомеханической системы идентичны, то равновесную систему считают идеальной. Равновесное состояние такой системы описывается уравнением Клапейрона
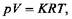
где р - давление газа в системе, Па; V - объем газа, м ; К - масса газа, кг; R -газовая постоянная, Дж/(кгК); Т- абсолютная температура, К.
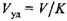 принимает вид принимает вид
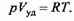
Преобразование энергии в системе, безусловно, подчинено закону сохранения энергии (первый закон термодинамики):

согласно которому поступившая в систему теплота dQ расходуется на изменение внутренней энергии (dU и совершение механической работы в связи с изменением объема системы: АрdV (где А - тепловой эквивалент механической работы). В удельных величинах уравнение (17.1) примет вид

В общем случае в координатах р - V произвольный термодинамический процесс можно представить в виде политропы с показателем степени п:
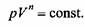
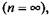 изотермический (п = 1). Процесс без теплообмена с внешней средой (dQ = 0) совершается по модифицированной политропе, называемой адиабатой, уравнение которой имеет вид изотермический (п = 1). Процесс без теплообмена с внешней средой (dQ = 0) совершается по модифицированной политропе, называемой адиабатой, уравнение которой имеет вид
 ) )
Показатель адиабаты к равен отношению удельных теплоемкостей при изобарном и изохорном процессах:
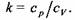
Для двухатомных газов и их смесей (воздух) к= 1,4.
Разность указанных теплоемкостей определяет другую термодинамическую константу:
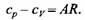
Сообщение термомеханической системе двух связанных между собой степеней свободы само по себе не делает процесс преобразования одной энергии в другую определенным. Например, нельзя без конца подогревать газ в цилиндре, повышая его давление - рано или поздно поршень выйдет из цилиндра или произойдет поломка. Для того чтобы преобразование энергии продолжалось неопределенно долго, систему необходимо периодически возвращать в исходное состояние.
Такое повторяющееся состояние термомеханической системы можно осуществить, если подвод и отвод теплоты, вызывающие соответствующие изменения объема газа, производить при различных положениях системы. Графики, отображающие эти процессы в координатах p - V или Т-S, образуют замкнутые кривые (рис. 17.1). Подобные процессы называют круговыми или циклами. В зависимости от направления цикла термомеханическую систему можно использовать в качестве теплового двигателя либо холодильной машины.
Понятие энтропии S ясно из определения теплоты Q как термической работы, совершенной системой:
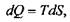

где Q - в Дж; S - в Дж/К. Температура Т здесь - качественный фактор интенсивности протекания процесса теплового взаимодействия между системой и средой (сравните с понятием силы, перемещающей тело в пространстве), а элементарное изменение энтропии dS является количественной мерой (фактором экстенсивности) состояния взаимодействующей системы (сравните с длиной пути, пройденного телом под действием силы).
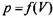 . Для выполнения этого условия формально необходимо, чтобы на координатной плоскости линия расширения цикла лежала выше линии сжатия. В этом случае работа расширения, соответствующая площади abcfga, превышает работу сжатия edfge (см. рис. 17.1, а), и в целом система совершает положительную работу против сил внешней среды. . Для выполнения этого условия формально необходимо, чтобы на координатной плоскости линия расширения цикла лежала выше линии сжатия. В этом случае работа расширения, соответствующая площади abcfga, превышает работу сжатия edfge (см. рис. 17.1, а), и в целом система совершает положительную работу против сил внешней среды.
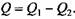 Значит, должен существовать не только источник (нагреватель), передающий теплоту рассматриваемой термомеханической системе, но и определенная система, воспринимающая неиспользованную в процессе преобразования энергии теплоту (холодильник). Значит, должен существовать не только источник (нагреватель), передающий теплоту рассматриваемой термомеханической системе, но и определенная система, воспринимающая неиспользованную в процессе преобразования энергии теплоту (холодильник).
Поскольку в круговом процессе не должно быть приращения внутренней энергии (все параметры и функции состояния системы в конце цикла равны первоначальным), по закону сохранения энергии теплота Q эквивалентна механической работе. Тогда термический КПД цикла

|