Кузнечно-штамповочное оборудованиеСиловой расчет балок и валов на упругом основании
Балка на упругом основании. Опора главного вала кривошипного пресса претерпевает упругие деформации в зависимости от действующей на вал нагрузки и свойств опоры. Это обстоятельство в сочетании с тем, что, во-первых, пролет опоры соответствует длине цапфы и, во-вторых, долевые и поперечные размеры цапфы соизмеримы, вносит значительные изменения в распределение сил.
Известно, что призматическая балка на упругом основании, нагруженная внешними силами, испытывает реактивное сопротивление со стороны основания. Установлено, чем больше прогиб балки, тем больше реакция основания. Для определения зависимости реакции от прогиба воспользуемся гипотезой Фусса-Винклера, согласно которой реакция основания пропорциональна прогибу оси балки в рассматриваемом поперечном сечении, т. е. упругое основание можно моделировать как множество пружин, перпендикулярных основанию и работающих независимо одна от другой. В этом случае реакцию основания на единицу площади призматической балки постоянной ширины можно определить по формуле
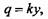
где к - коэффициент податливости основания, или коэффициент постели, МН/м ;
у - прогиб основания.
Коэффициент податливости характеризует силу, которую необходимо приложить к единице площади основания, чтобы дать ему осадку, равную единице длины. Коэффициент податливости зависит от материала и конструктивного оформления опоры. В частности, в расчете валов КШМ рекомендуется принимать к = 125 ГН/м3.
Помимо гипотезы о соотношении между реакцией и прогибом основания при расчете балок на упругом основании принимают два допущения: 1) основание оказывает равные реакции при прогибах балки как вниз, так и вверх, т. е. неразрывно связано с балкой; 2) балка является достаточно жесткой и не подвержена поперечному сжатию или растяжению.
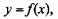 а затем составляют уравнения моментов и сил. а затем составляют уравнения моментов и сил.
Дифференциальное уравнение моментов для изогнутой балки под действием сосредоточенных сил имеет вид
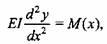
где Е - модуль упругости материала балки; /-момент инерции сечения балки.
Поскольку М(х) неизвестно, необходимо связать прогиб с нагрузкой. Для этого продифференцируем дважды уравнение моментов:
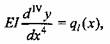
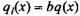 - интенсивность распределенной нагрузки по длине балки, т. е. - интенсивность распределенной нагрузки по длине балки, т. е.
сила, действующая на единицу длины; Ъ - ширина балки.
Реакция основания всегда направлена противоположно прогибу:

Дифференциальное уравнение прогиба при заданной интенсивности нагрузки имеет вид
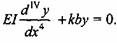
Если провести подстановку z = хт, обозначив
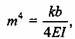
то дифференциальное уравнение прогиба примет вид

Общий интеграл уравнения (3.17), т. е. уравнение линии прогиба, имеет следующее выражение:
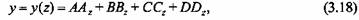

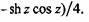
Остальные уравнения получаем дифференцированием (3.18). Для угла поворота оси балки имеем
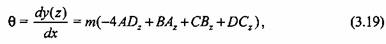
для изгибающего момента с учетом знаков нагрузки и прогиба находим
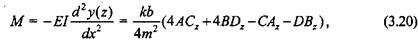
а для поперечной силы получаем
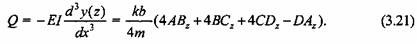
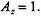 Тогда из уравнений (3.18)-(3.21) получаем Тогда из уравнений (3.18)-(3.21) получаем
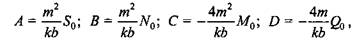
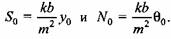
Таким образом, общее решение для балки на упругом основании имеет вид
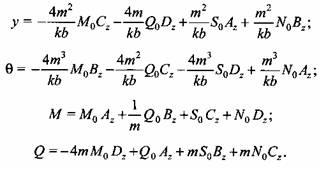
Коленчатый вал. Расчет коленчатого вала представляет сложную задачу. Необходимо принять ряд допущений с тем, чтобы свести задачу к решению призматической балки постоянного сечения на упругом основании. Следуя А.Ф. Нистратову, впервые предложившему расчет валов КШМ, будем рассматривать коленчатый вал как ступенчатую балку, а цапфы вала в опорах скольжения - как раздельные балки постоянного сечения, заделанные в сплошное упругое основание и нагруженные по концам сосредоточенными силами и изгибающими моментами.
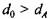 для соблюдения условия равной жесткости пролет между опорами несколько занижают и принимают равным расстоянию по средним линиям щек. для соблюдения условия равной жесткости пролет между опорами несколько занижают и принимают равным расстоянию по средним линиям щек.
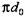 . Для опорных цапф валов кривошипных прессов следует принимать меньшее значение в связи с тем, что края вкладышей подшипника скруглены во избежание защемления вала. Следовательно, на единицу длины цапфы действует сила . Для опорных цапф валов кривошипных прессов следует принимать меньшее значение в связи с тем, что края вкладышей подшипника скруглены во избежание защемления вала. Следовательно, на единицу длины цапфы действует сила
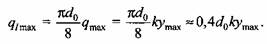
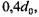 а в случае, когда в опоре отсутствует а в случае, когда в опоре отсутствует
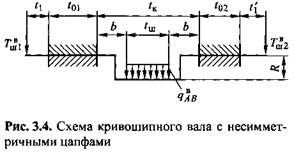
Сделанные допущения позволяют выбрать схему, являющуюся расчетным аналогом одноколенчатого вала с двусторонним зубчатым приводом и маховиком на приемном валу. Решение балки-аналога проведем для вертикальной плоскости с присвоением верхнего индекса в вертикальным составляющим сил и изгибающих моментов.
 -длины вкладышей опорных подшипников. -длины вкладышей опорных подшипников.
Если теперь действие внешних сил заменить изгибающими моментами и поперечными силами, то получим расчетную схему балки-аналога, состоящую из трех участков (рис. 3.5):
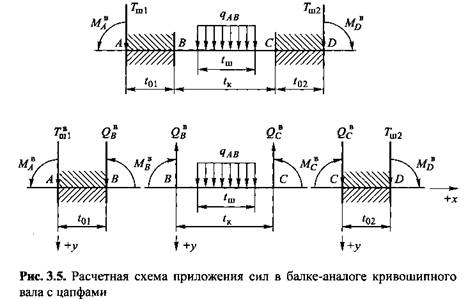
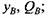
участок ВС - балка с заделанными концами и пролетом между опорами
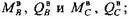
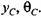
Рассмотрим часто встречающуюся конструкцию одноколенчатого вала с односторонним зубчатым приводом и маховиком на приемном валу. В соответствии с расчетной схемой (см. рис. 3.5) принимаем
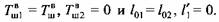
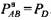 , а нормальная сила, приложенная к зубу колеса, , а нормальная сила, приложенная к зубу колеса,
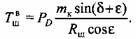
Распределение изгибающих моментов и поперечных сил по участкам одно-коленчатого вала с односторонним зубчатым приводом характеризуют следующие уравнения:
1) консольная часть балки:
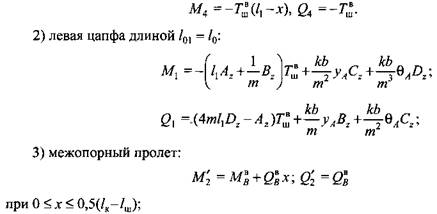

Прогибы и углы поворота, входящие в эти уравнения, можно определить по формулам
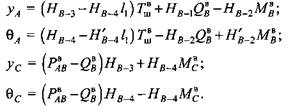
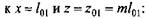
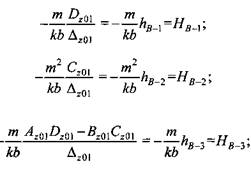
Коэффициенты при силовых факторах в уравнениях для прогибов и углов поворота зависят от параметров первого участка балки-аналога и отнесены
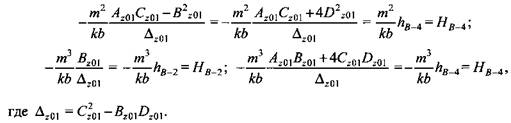
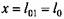 (см. рис. 3.4), (см. рис. 3.4),
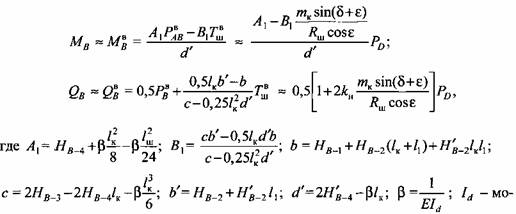

 (см. рис. 3.4), (см. рис. 3.4),
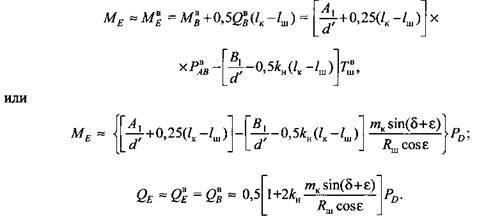
Наконец, в сечении РР, расположенном посредине межопорного пролета, т. е. при х = 0,5/к (см. рис. 3.4),
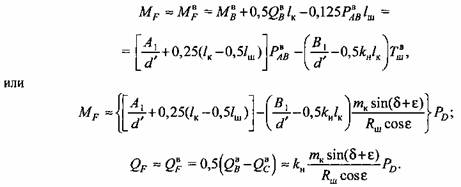
Распределение крутящих моментов по участкам одноколенчатого вала с односторонним зубчатым приводом характеризуют следующие уравнения:
1) по длине консоли и правой цапфы -
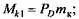
2) по длине левой щеки -
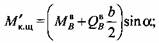
3) по длине коленной шейки -
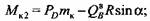
4) по длине правой щеки -
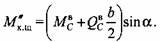
Правая цапфа коленчатого вала свободна от скручивания.
|