Кузнечно-штамповочное оборудованиеПроектирование кузнечно-штамповочных машин
Кривошипные прессы
Проектирование многозвенных исполнительных механизмов.
Проектирование многозвенных исполнительных механизмов кривошипных прессов включает в себя:
синтез кинематической схемы;
предварительное назначение ее параметров, т. е. размеров элементов и их исходных положений;
корректировку параметров кинематической схемы до получения желательных значений параметров закона движения ползуна.
Решение двух первых задач носит творческий характер и опирается на существующий опыт проектирования, общетехнические представления и интуицию проектировщика (см. § 2.5). Решение третьей задачи поддается формализации, а подходы к нему одинаковы для механизмов с любой кинематической схемой. При этом к результатам проектирования на первых двух этапах не предъявляют высоких требований в отношении их качества. Нужно получить лишь работоспособный вариант, который будет улучшен при решении третьей задачи.
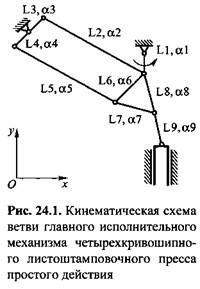
Список значений параметров закона движения ползуна определяется назначением механизма. Исполнительные механизмы прижимных ползунов листоштамповочных прессов должны обеспечивать необходимые значения хода ползуна, угла опережения прижимного ползуна, продолжительности выстаивания в нижнем положении, отхода ползуна от крайнего нижнего положения во время выстаивания, а многозвенные главные исполнительные механизмы самих прессов - необходимый ход и минимальную скорость ползуна при деформировании заготовки.
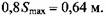
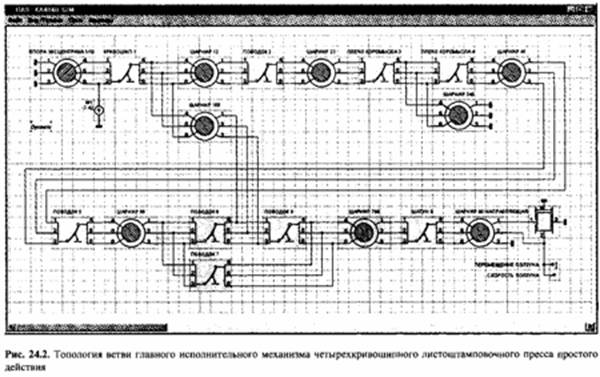
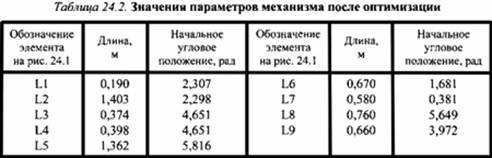
Предварительно назначенные параметры кинематической схемы и обозначения элементов на топологии (рис. 24.2) приведены в табл. 24.1. Угловые положения элементов L6, Ь7 и L8 являются зависимыми от других параметров и вычисляются через них по тригонометрическим зависимостям. Вращение кривошипа механизма воспроизводится источником фазовой переменной типа потенциала (элемент W1), в данном случае угловой скорости (см. рис. 24.2). Вывод результатов моделирования осуществляется индикаторами ПЕРЕМЕЩЕНИЕ ПОЛЗУНА и СКОРОСТЬ ПОЛЗУНА. Согласно результатам моделирования (рис. 24.3, а), максимальная скорость ползуна на этапе рабочего хода равна 0,542 м/с, минимальная - 0,425 м/с. Задачу корректировки параметров кинематической схемы можно поставить и решить как задачу безусловной оптимизации. Критериями оптимизации приняты максимальная скорость ползуна на участке рабочего хода и отклонение его полного хода от заданного. Целевую функцию формируют как аддитивный критерий со следующими весовыми коэффициентами при частных критериях: 0,00001 для максимальной скорости ползуна на участке рабочего хода и 0,99999 для отклонения полного хода ползуна от заданного. В качестве параметров оптимизации принимают длины элементов кинематической схемы и их начальные угловые положения. Оптимизацию осуществляют методом Нелдера-Мида. Согласно результатам моделирования (рис. 24.3, б), максимальная скорость ползуна на этапе рабочего хода стала 0,416 м/с, что в 1,3 раза
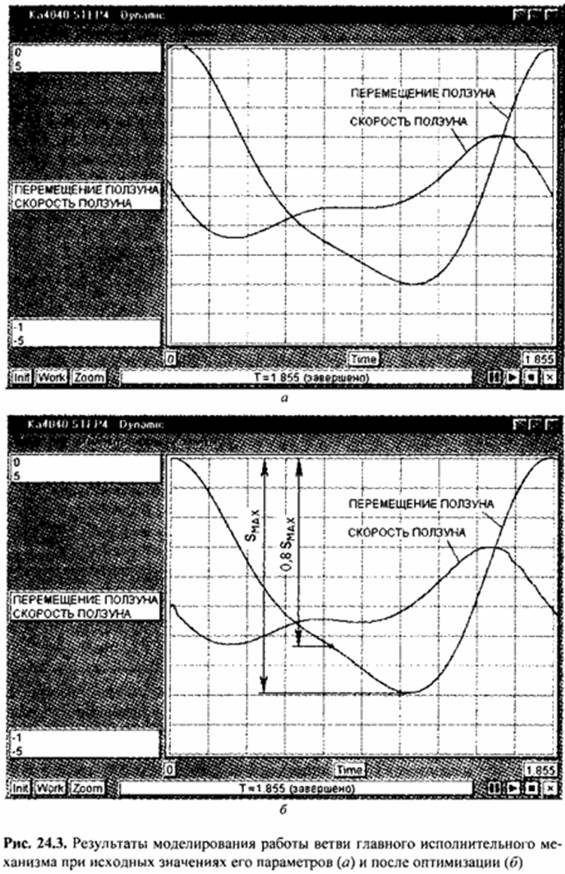
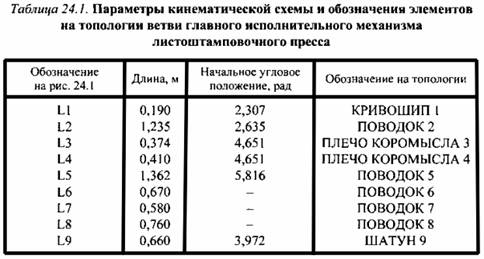
меньше исходной. Оптимизация выполнена за 139 шагов. Значения параметров механизма, которые получены в результате оптимизации, приведены в табл. 24.2.
Описанный подход сохраняется для многозвенных исполнительных механизмов любой структуры и сложности. Отличия в решении третьей задачи проектирования многозвенных исполнительных механизмов иной структуры будут связаны с формированием целевой функции в соответствии с требуемыми служебными свойствами механизма и назначением прямых и функциональных ограничений.
Основной задачей при проектировании исполнительных механизмов относительно простой структуры (кривошипно-ползунных, кривошипно-коленных, кривошипно-шарнирных и др.) является кинематический анализ. Ее решение является составной частью решения задачи проектирования многозвенных исполнительных механизмов кривошипных прессов, которое рассмотрено выше.
Проектирование кулачковых механизмов. Математическое моделирование позволяет отказаться от поиска наилучшего закона движения толкателя кулачкового механизма среди ограниченного множества таких законов и решить задачу синтеза профиля кулачка в общей постановке: найти оптимальный профиль ку-
лачка по выбранному критерию или их совокупности. Для этого конструктивный профиль кулачка задают в полярной системе координат значениями угловых координат, которые отсчитывают от точки, принятой в качестве начальной, и их радиусов-векторов. Координаты вводят как параметры математической модели кулачкового механизма KULMD. Участки профиля между точками, задающими конструктивный профиль кулачка, определяются кубическими сплайнами:
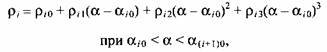
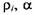 - текущий радиус-вектор и угловая координата какой-либо точки про- - текущий радиус-вектор и угловая координата какой-либо точки про-
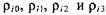 - коэффициенты сплайна; i - порядковый номер - коэффициенты сплайна; i - порядковый номер
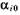 - начальная точка /-го участка профиля. - начальная точка /-го участка профиля.
Сплайны рассчитываются в математической модели кулачкового механизма из условия непрерывности функции, описывающей весь профиль кулачка, а также первой и второй ее производных по угловой координате и используются для вычисления в модели координат точек контакта (при его наличии) ролика с кулачком. Весь профиль кулачка в общем случае состоит из участков постоянного радиуса и рабочих участков. Основой методики синтеза профиля кулачка является его оптимизация на каждом из рабочих участков по одному или нескольким критериям. Первоначально каждый из оптимизируемых участков задают крайними точками. Затем выполняют моделирование.
Оптимизируемый участок делится в угловом отношении пополам с получением при этом новой точки участка. По коэффициентам сплайна вычисляется радиус-вектор этой дополнительной точки. Проводится оптимизация профиля по выбранному критерию с принятием новой точки в качестве управляемого параметра. Каждый из участков, полученных при делении рабочего участка, вновь делится пополам с образованием новых точек профиля - второй этап оптимизации. На этом и последующих этапах радиус-векторы всех новых точек принимаются в качестве управляемых параметров. Каждый следующий этап оптимизации выполняется после очередного деления участков. Синтез профиля кулачка проиллюстрируем на трех примерах.
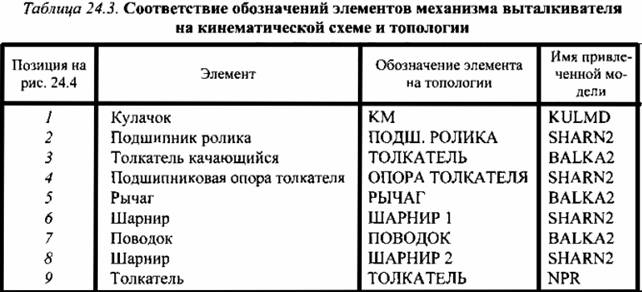
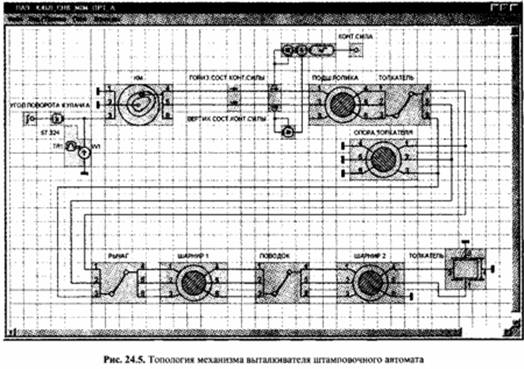
1. Найти профиль кулачка привода механизма выталкивателя штамповочного автомата, обеспечивающий минимальное значение контактных сил в паре кулачок - ролик и повышающий долговечность механизма. Кинематическая схема механизма приведена на рис. 24.4.
Синтез профиля кулачка выполним с помощью математической модели механизма. Соответствие элементов кинематической схемы и топологии механизма (рис. 24.5) показано в табл. 24.3. Для оптимизации профиля кулачка используем метод Гаусса-Зейделя.
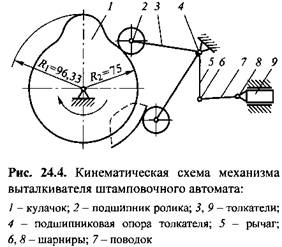
На рис. 24.6 приведены результаты моделирования рабочего хода механизма выталкивателя до и после оптимизации профиля. Максимальное значение контактной силы в паре кулачок - ролик для найденного профиля кулачка составило 518,09 Н.
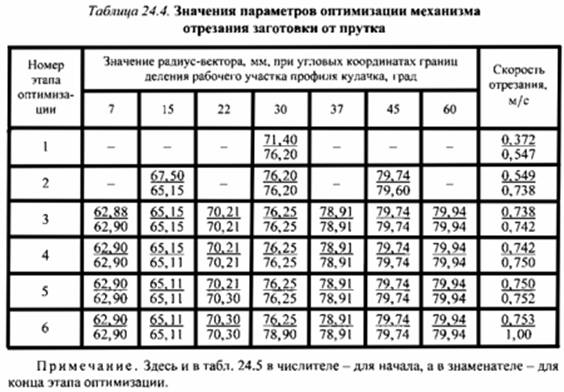
2. Найти профиль кулачка привода штамповочного автомата для механизма отрезания заготовки от прутка, обеспечивающий максимальную скорость ножа отрезного инструмента втулочного типа при его перемещении от исходного положения на 2,9 мм. Радиусы участков постоянного радиуса равны 62,5 и 80 мм; угол рабочего участка профиля кулачка 60°.
Постановка задачи связана с тем, что с повышением скорости отрезания повышается качество торца заготовки, а втулочный типа отрезного инструмента ограничивает ход ножа до начала отрезания.

Оптимизацию выполним методом Гаусса-Зейделя. Данные процесса оптимизации приведены в табл. 24.4. В таблице опущены промежуточные данные для каждого этапа, а указаны значения для его начала (числитель) и конца (знаменатель). Видно, что в результате синтеза профиля кулачка с использованием математического моделирования удалось достичь скорости отрезания 1 м/с при ходе разгона 2,9 мм.
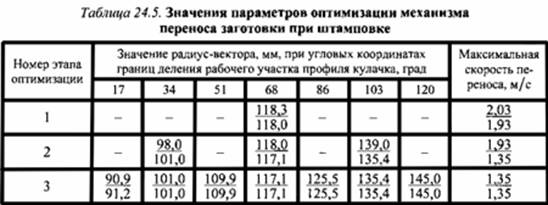
3. Найти профиль кулачка привода механизма переноса заготовки между позициями штамповки, обеспечивающий минимальное значение максимальной скорости переноса. Радиусы участков постоянного радиуса равны 87,353 и 150 мм; угол рабочего участка профиля кулачка 137°.
Постановка задачи связана с тем, что движение заготовки происходит по дуге окружности с действием на нее центробежных сил, которые могут привести к выбросу заготовки из захвата.
Оптимизацию выполним методом Гаусса-Зейделя. Ее результаты приведены в табл. 24.5, причем данные указаны для начала (числитель) и конца (знаменатель) каждого этапа оптимизации. Видно, что в результате синтеза профиля кулачка с использованием математического моделирования удалось снизить скорость переноса заготовки с 2,03 м/с до 1,35 м/с, т. е. в 1,503 раза, а нормальное ускорение и центробежную силу - в 2,26 раза.
Расчеты элементов пресса на прочность и жесткость
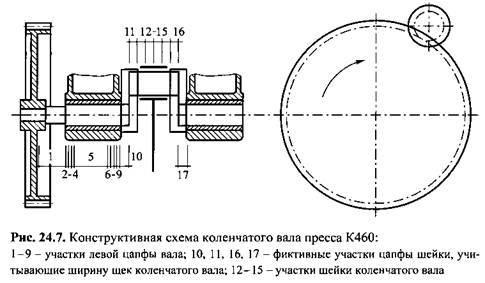
Расчет допускаемой силы на ползуне по усталостной прочности коленчатого вала. Рассмотрим этот расчет на примере коленчатого вала пресса К460 с номинальным усилием 0,63 МН и максимальным ходом ползуна 0,4 м. Его конструктивная схема показана на рис. 24.7.
Вал выполнен из стали 40Х. Для расчета допускаемой силы на ползуне необходимо создать математическую модель коленчатого вала и смежных устройств, влияющих на его прочность: зубчатой передачи и главного исполнительного механизма. Топология вала приведена на рис. 24.8. Для полноценного учета упругих свойств вала с подшипниками цапфы и шейку вала в зоне их контакта с подшипниками разделим на 15 участков. Это позволит также определить закон, по которому сила распределяется по длине опор и шейки коленчатого вала.

В топологии модели участки вала представлены элементами РКЛ-РК25 (модель FRVL, см. табл. 23.1), а прилегающие к ним участки подшипников элементами SН1-SН25 (модель SНАRN2). В зонах участков 2-4, 6-9, 12-15 сосредоточиваются рабочие нагрузки, и поэтому их протяженность меньше остальных. Щеки вала представлены элементами ВЬ и ВК (модель ВАЬКАЬШ). Ширину щек учитываем фиктивными участками 10, 11, 16, 17 цапф и шейки вала. Зубчатая передача представлена элементом 2Р (модель 2АСРСЫ), главный исполнительный механизм - моделями шатуна (ВАЬКАЬШ), направляющих (NPR) и технологической нагрузки ( TNGK ) или постоянной силы (ТЫ). Враще ние вала воспроизводим с помощью модели источника фазовой переменной ти па потенциала (элемент W ), в данном случае угловой скорости.
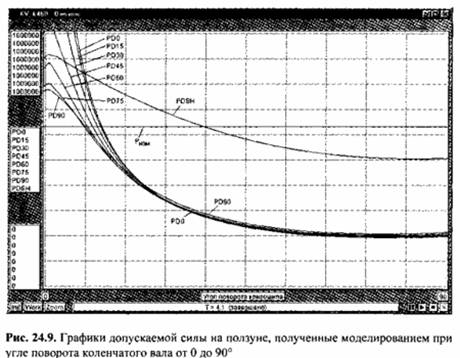
Модель однородного цилиндрического участка вала FRVL дает возможность определить допускаемую силу на ползуне по прочности коленчатого вала. Для расчета допускаемой силы на ползуне введем постоянную нагрузку на пол зуне, равную номинальному усилию пресса и направленную вверх. Приложение постоянной нагрузки воспроизводим с помощью модели источника фазовой переменной типа потока (элемент ТС). При этом в полюсах модели FRVL на каж дом шаге интегрирования вычисляются в виде фазовых переменных типа потока поперечные силы, изгибающие и крутящие моменты, осевые силы сжатия. В модели FRVL по формулам (3.22) и (3.25) вычисляются нормальные и полные касательные напряжения, а по формуле (3.26) - запас прочности коленчатого вала в выбранных сечениях. Допускаемая сила на ползуне определяется как расчетная переменная путем умножения номинального усилия пресса на вычислен ный запас прочности и деления полученного значения на требуемый запас прочности с учетом коэффициента долговечности аналогично его учету в (3.27). Все названные вычисления выполняются для углов координации ф, рав ных 0, 15, 30, 45, 60, 75 и 90° одновременно. Вывод графиков допускаемой силы на ползуне по прочности коленчатого вала для каждого из указанных углов ко ординации осуществляется с помощью универсальных индикаторов РБ0, Р D 15, Р D 30, Р D 45, Р D 60, Р D 75, Р D 90 для сечения В-В и Р DS Н для сечения Е-Е (рис. 24.8; см. также рис. 3.4).
Графики допускаемой силы на ползуне, полученные моделированием при угле поворота коленчатого вала от 0 до 90°, представлены на рис. 24.9. Горизон тальная прямая соответствует номинальному усилию пресса. Как видно на графиках, на различных этапах работы исполнительного механизма прочность вала в сечении В-В определяется точками вала с различными значениями угла координации. Так, при угле поворота коленчатого вала от 0 до 6,17° точка сечения В-В, определяющая прочность вала, имеет угол координации ф = 90°; от 6,17 до 17,34° - ф = 75°; от 17,4 до 26,4° - ср = 60°; от 26,4 до 33,1° - ср = 45°; от 33,1 до 38,9° - ф = 30° и от 38,9 до 90° - ф = 0°. График допускаемых сил на ползуне представляет собой огибающую полученных кривых, составленную из указанных участков.
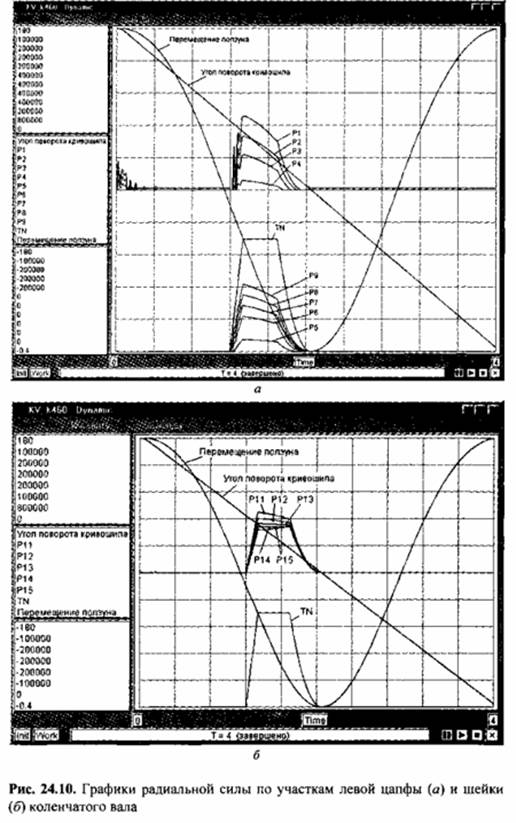
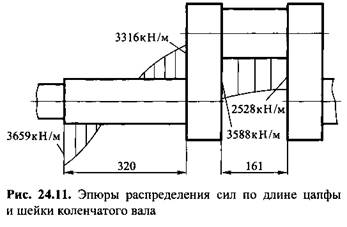
Для нахождения распределения нагрузки в цапфах и шейке выводятся значения радиальной силы на участках цапф и шейки при помощи универсальных индикаторов Р1 - Р15. Нагружение исполнительного механизма осуществляется с использованием модели технологической нагрузки ТТЧОК (элемент ТЖ}). Полученные при моделировании графики распределения радиальной силы по участкам левой цапфы и шейки вала приведены на рис. 24.10.
Эти графики позволяют построить эпюры распределения сил по длине цапфы и шейки. Для момента их максимального значения (7 = 1,34 с) они приведены на рис. 24.11. Радиальные силы определены через их горизонтальные и вертикальные составляющие и условно показаны в вертикальной плоскости.
При решении задач о допускаемой силе на ползуне пресса по прочности коленчатого вала полноценно учитывается влияние как вертикальных, так и горизонтальных составляющих радиальных сил, форма, размеры и упругие свойства коленчатого вала, упругие свойства подшипниковых опор вала и кривошипной головки шатуна, нормальные силы в зубчатой передаче и сил трения в зацеплении, моменты сил трения в подшипниковых опорах и шарнирах исполнительного механизма, силы трения в направляющих, силы тяжести всех элементов,
представленных в модели коленчатого вала и смежных элементов, фактическое распределение радиальной силы вдоль осей цапф и кривошипной головки шатуна, зазоры в опорах и кривошипной головке шатуна.
В случае получения результата, не удовлетворяющего проектировщика, он имеет возможность быстро и оперативно изменить по своему усмотрению параметры элементов математической модели, например диаметры цапф или шейки, прочностные свойства материала коленчатого вала, другие параметры.
Рассмотренный подход к решению задачи о допускаемой силе на ползуне пресса по прочности коленчатого вала применим к случаям любых конструктивных разновидностей коленчатых валов, схем привода, вариантов размещения маховика пресса.
Расчет допускаемой силы на ползуне по прочности зубчатой передачи. В качестве примера рассмотрим тихоходную зубчатую передачу пресса К460 (см. рис. 24.7). Для расчета допускаемой силы на ползуне по прочности зубчатой передачи будем использовать модель, приведенную на рис. 24.8, которая содержит элемент 2Р (модель зубчатого эвольвентного внешнего зацепления 2АСРСК).
Модель 2АСРСК дает возможность определить допускаемую силу на ползуне по прочности зубчатой передачи. Для расчета этой силы, как и при расчете допускаемой силы на ползуне по усталостной прочности коленчатого вала, введем постоянную нагрузку на ползуне, равную номинальному усилию пресса и направленную вверх. Приложение постоянной нагрузки воспроизводится с помощью модели источника фазовой переменной типа потока (элемент ТО). В полюсах модели 2АСРСК на каждом шаге интегрирования вычисляются радиальные силы и крутящие моменты в виде фазовых переменных типа потока. При этом учитываются упругие свойства контакта зубьев, силы трения в зацеплении, их распределенность по длине рабочей части линии зацепления, изменения направлений сил и моментов при реверсировании передачи, возможные радиальные перемещения центров шестерни и элементов.
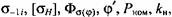 вводимых в качестве вводимых в качестве
параметров модели.
Допускаемая сила на ползуне пресса по каждому виду прочности зубчатой передачи определяется как расчетная переменная путем умножения номинальной силы пресса на вычисленный запас прочности и деления на требуемый запас прочности, вводимый как параметр.
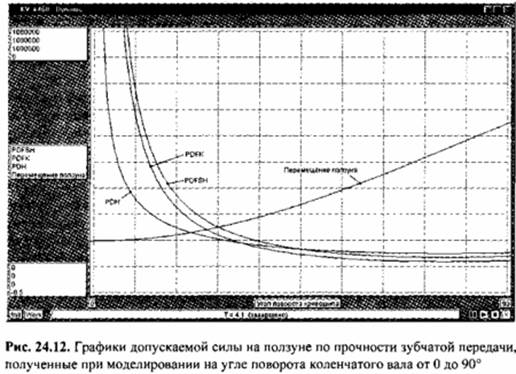
Графики допускаемой силы на ползуне, рассчитанные по прочности зубчатой передачи при моделировании на угле поворота коленчатого вала от 0 до 90°, приведены на рис. 24.12.
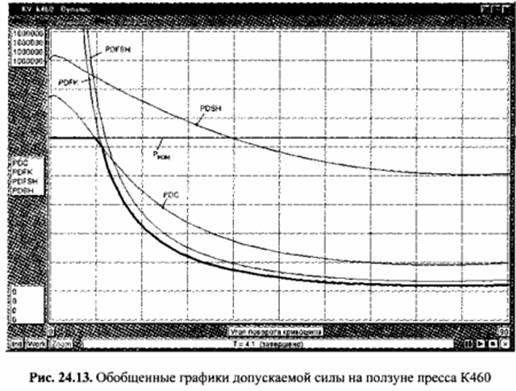
На рис. 24.13 показаны графики допускаемой силы на ползуне пресса К460, построенные с учетом представленных на рис. 24.9 и 24.12 данных. На рис. 24.12 и 24.13 обозначены: РБР8Н, РБРК - графики допускаемой силы на ползуне, рассчитанные по изгибной прочности зуба шестерни и колеса соответственно; РБН -график допускаемой силы на ползуне, определенный по контактной выносливости
 - номинальное усилие пресса. - номинальное усилие пресса.
Согласно полученным результатам, допускаемая сила на ползуне на разных участках графика определяется номинальным усилием пресса, прочностью цапфы коленчатого вала и изгибной прочностью колеса зубчатой передачи.
Поскольку зубчатая передача открытая, при построении графика допускаемой силы на ползуне не принят во внимание график РDН. Степень учета различных факторов при расчете допускаемой силы на ползуне по прочности зубчатой передачи факторов такой же, что и при расчете допускаемой силы по прочности коленчатого вала.
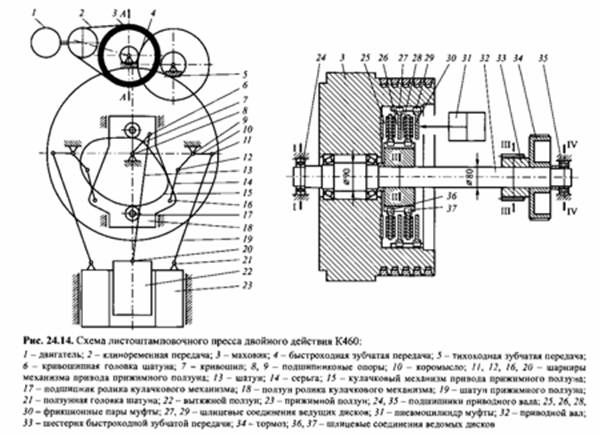
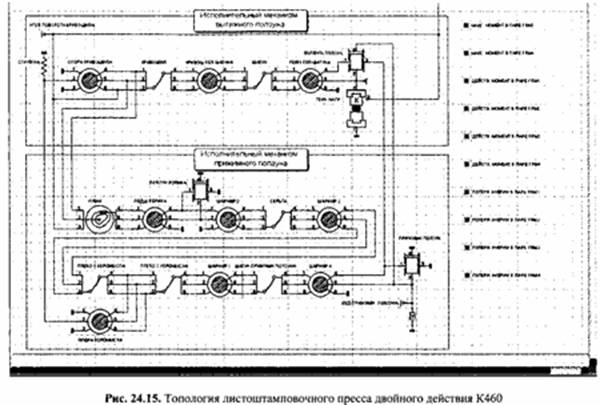
Расчет валов, подшипников, зубчатых передач кривошипных прессов. В качестве примера рассмотрим листоштамповочный пресс двойного действия К460 с номинальной силой 0,63 МН, полным ходом вытяжного ползуна 0,4 м и числом ходов в минуту 15. Его кинематическая схема показана на рис. 24.14. Особенностью пресса является привод прижимного ползуна от кулачкового механизма.
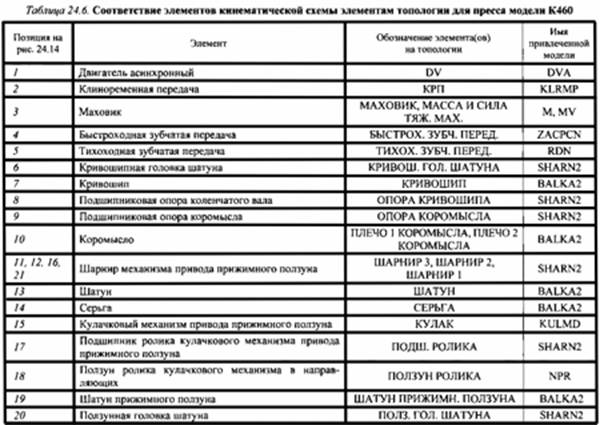
Топология пресса (рис. 24.15) представлена во фрагментах: Привод, Исполнительный механизм вытяжного ползуна, Исполнительный механизм прижимного ползуна, Система управления. Соответствие элементов кинематической схемы элементам топологии показано в табл. 24.6.
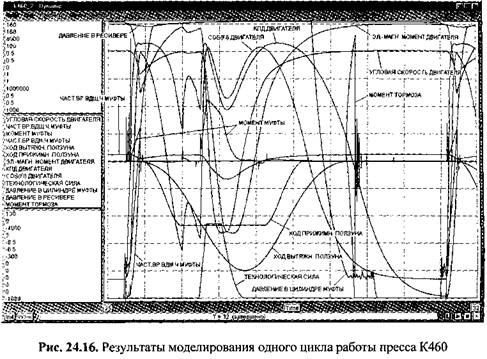
Моделирование работы пресса осуществляется в два периода - разгон маховика и один или несколько циклов работы пресса. На рис. 24.16 показаны результаты моделирования одного цикла работы пресса.
Расчет вала. Для выполнения расчета в модели пресса необходимо представить сам вал, его подшипниковые опоры и нагружающие элементы. Вал моделируется однородными участками, расположенными между его опорами и нагружающими элементами. В качестве примера рассмотрим расчет приводного вала (материал - сталь 40Х) пресса К460 (см. рис. 24.14, сечение А-А).
Нагружающими элементами являются клиноременная передача, маховик, являющийся ведомым шкивом клиноременной передачи, и быстроходная зубчатая передача. Вал выполнен двухопорным на подшипниках качения, размещенных на его концах.
В модели пресса вал 32 (см. рис. 24.14) представлен тремя участками:
между левой подшипниковой опорой 24 (сечение 1-1) и маховиком 3 (сечение П-Н) - элемент УЧАСТОК ВАЛА 1;
между маховиком и шестерней 33 (сечение Ш-Ш) быстроходной зубчатой передачи 4 - элемент УЧАСТОК ВАЛА 2;
между шестерней быстроходной зубчатой передачи и правой подшипниковой опорой 35 (сечение IV-IV) - элемент УЧАСТОК ВАЛА 3.
Элементы УЧАСТОК ВАЛА 1 - УЧАСТОК ВАЛА 3 представлены моделью однородного цилиндрического участка вала FRVL, а нагружающие вал элементы следующим образом:
клиноременная передача 2 - элементом КРП (модель КLRМР);
маховик 3 - элементами МАХОВИК (модель маховой массы М) и МАССА И СИЛА ТЯЖ. МАХ. (модель инерционной и тяготеющей массы МV);
зубчатая передача 4 - элементом БЫСТРОХ. ЗУБЧ. ПЕРЕД, (модель 2АСРСЫ);
подшипниковые опоры 24 и 35 - элементами ПОДШ. 1 и ПОДШ. 2 (модель 8НАКШ);
тормоз 34 - элементом ТОРМОЗ (модель ТОRМOZ).
Таким образом, в модели пресса воспроизводится нагружение вала силой натяжения ветвей клиноременной передачи, силой тяжести маховика, нормальными силами и силами трения в зубчатой передаче, а также моментами этих сил, реакциями подшипниковых опор и моментами трения в них, динамическим моментом маховика при его замедлении, моментом торможения. При этом в полюсах модели РЯУЬ вычисляются в виде фазовых переменных типа потока поперечные силы, изгибающие и крутящие моменты, осевые силы сжатия. В модели РКУЬ по формулам (3.22) и (3.25) определяются нормальные и касательные напряжения, средние напряжения цикла (от действия осевых сил сжатия растяжения и поперечных сил) и амплитуды напряжений (от изгибающих и крутящих моментов), эквивалентные нормальные и касательные напряжения.
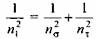 рассчитывается запас прочности. Все указанные вычисления выполняются на каждом шаге интегрирования для сечений вала, соответствующих каждому его концу. В связи с непостоянством на-гружения вала в течение цикла работы пресса вычисляется эквивалентный запас прочности. Он определяется в процессе моделирования по итогам выполненной его части и сам является переменной величиной. Во внимание следует принимать значения эквивалентного запаса прочности в конце любого цикла работы пресса. Для исключения влияния нестационарной части работы пресса, например периода разгона маховика, вычисление эквивалентного запаса прочности начинается в фиксированный момент модельного времени, значение которого вводят как один из параметров модели FRVL. Его значение можно принимать равным времени начала первого цикла работы пресса. рассчитывается запас прочности. Все указанные вычисления выполняются на каждом шаге интегрирования для сечений вала, соответствующих каждому его концу. В связи с непостоянством на-гружения вала в течение цикла работы пресса вычисляется эквивалентный запас прочности. Он определяется в процессе моделирования по итогам выполненной его части и сам является переменной величиной. Во внимание следует принимать значения эквивалентного запаса прочности в конце любого цикла работы пресса. Для исключения влияния нестационарной части работы пресса, например периода разгона маховика, вычисление эквивалентного запаса прочности начинается в фиксированный момент модельного времени, значение которого вводят как один из параметров модели FRVL. Его значение можно принимать равным времени начала первого цикла работы пресса.
Эквивалентные запасы прочности вычисляются для каждого конца участка вала как расчетные переменные и выводятся с помощью универсальных индикаторов. Согласно рис. 24.14, универсальный индикатор NA выводит вычисляемый запас прочности в сечении вала II-II с левой его стороны, а индикатор NB -с правой. При этом правая сторона сечения П-П в отличие от левой нагружена динамическим моментом маховика. Универсальный индикатор NC выводит вычисляемый запас прочности в сечении вала Ш-Ш с левой, а индикатор ND -с правой его стороны (см. рис. 24.15).
На рис. 24.17 показаны полученные моделированием результаты расчета вала на прочность в виде графиков NA, NB, NC, ND эквивалентных запасов прочности для соответствующих сечений вала в двух циклах работы пресса. Эквивалентные запасы прочности в конце циклов работы пресса (t = 31,35915 с) имели следующие значения: NA = 3,090848; N6 = 2,145247; N0-1,699190; ND= 1,711759. Полученные значения запасов прочности приводного вала соответствуют рекомендуемым (см. табл. 3.2).
Для определения запасов прочности валов при выполнении прессом различных технологических операций необходимо моделирование работы пресса в составном цикле, содержащем циклы с графиками технологической силы каждой операции. Во внимание следует принимать значения эквивалентного запаса прочности в конце составного цикла работы пресса.
При определении запасов прочности валов путем математического моделирования учитываются статические и динамические составляющие рабочих нагрузок на валах, которые определяются свойствами элементов, воспроизводимых привлеченными моделями; асимметрия циклов нагружения; коэффициенты
концентрации напряжений; влияние размеров; качество обработки поверхностей; переменный характер нагружения валов в течение цикла; силы трения в кинематических парах; кроме того, автоматически раскрывается статическая неопределимость для многоопорных валов.
Линейные и угловые упругие перемещения сечений вала могут привести к недопустимым изменениям зазоров и перекосам в зубчатых передачах, недопустимым перекосам в подшипниках и другим отрицательным последствиям. Поэтому они должны быть определены. Полюса 1, 2 модели РКУЬ (см. табл. 23.1) соответствуют линейным координатам перемещения сечения одного из концов участка вала в направлениях, перпендикулярных его оси; полюса 7, 8 - то же для сечения другого конца участка вала. Полюса модели РКУЬ 4, 5 и 8, 9 соответствуют угловым координатам поворота тех же сечений в плоскостях, перпендикулярных его оси.
При интегрировании в узлах топологии, к которым присоединены названные полюса, вычисляются линейные и угловые скорости, являющиеся составляющими полных скоростей в разложении по координатным осям. Их интегрирование позволяет получить линейные и угловые перемещения сечений по всем названным координатам. Они, как и скорости, будут составляющими полных перемещений в разложении по тем же координатным осям. Полные перемещения получаются в результате извлечения квадратного корня из суммы квадратов перемещений по соответствующим координатным осям. Интегрирование линейных и угловых скоростей и вычисление полных перемещений выполняются посредством математических операций над фазовыми и расчетными переменными, встроенными в программный комплекс ПА9. Для этого на поле схемы размещают графические образы элементов соответствующих математических операций, входы и выходы которых соединяют. Результаты вычислений линейных и угловых упругих перемещений сечений вала выводятся с помощью индикаторов (см. рис. 24.15, элемент FE), которые присоединяют к выходам совокупности элементов, осуществляющих математические преобразования (см. на рис. 24.15
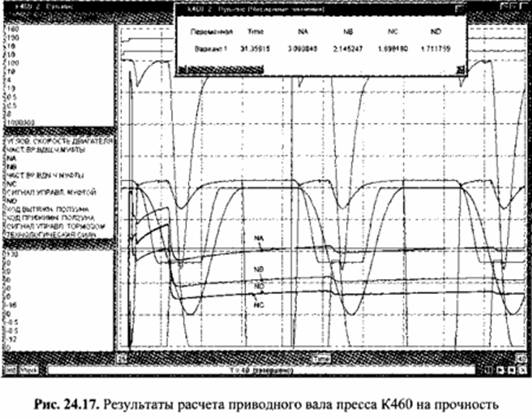
На рис. 24.18 в качестве примера показаны полученные моделированием графики составляющих угловых перемещений вала FEХ и FIY в горизонтальной X и вертикальной V плоскостях в сечении вала ГУ-ГУ у правой подшипниковой опоры (см. рис. 24.14) и полного углового перемещения FE в том же сечении.
Максимальные угловые перемещения имеют место в зоне нарастания деформирующей силы при t = 26,86768 с и равны FIX = 0,001855 рад, FIX = 0,002585 рад, FI = 0,003182 рад. Согласно литературным данным, допустимый угол поворота сечения вала для однорядных шариковых подшипников составляет 0,005 рад. Следовательно, полученное расчетом значение угла поворота сечения вала у левой подшипниковой опоры вала является допустимым.
При определении линейных и угловых упругих перемещений сечений вал путем математического моделирования учитываются статические и динамиче кие составляющие рабочих нагрузок на валах, определяемые свойствами во производимых привлеченными моделями элементов, упругие деформации и зоры в кинематических парах элементов, представленных в модели пресса.
Расчет подшипников качения. В качестве примера рассмотрим р; чет подшипников приводного вала пресса К460 (см. рис. 24.14). Вал смонтир ван на подшипниках 24 (подшипник серии 315, С= 132 000 Н) и 35 (подшипн серии 2316, С = 240 000 Н).
В модели пресса (см. рис. 24.15) подшипниковые опоры приводного ва представлены элементами ПОДШ. 1 и ПОДШ. 2 модели шарнира SHARN В полюсах модели SHARN2 вычисляются в виде фазовых переменных типа тока радиальные силы упругого взаимодействия внешнего и внутреннего ментов подшипника, а также момент трения. В модели SНАRN2 с учет температурного коэффициента и коэффициента вращения определяется экви] лентная радиальная сила, чем учитывается непостоянство радиальной силы частоты вращения. Коэффициент безопасности в расчетах не используют, как определяющая его динамичность процесса воспроизводится при моделировании. Затем рассчитываются ресурсные параметры: расчетная динамическая грузоподъемность при базовом числе 106 оборотов подшипника и срок службы подшипника в часах. Все указанные вычисления выполняются на каждом шаге интегрирования. Ресурсные параметры определяются в процессе моделирования по итогам выполненной его части, и сами являются переменными величинами. Во внимание следует принимать их значения в конце любого цикла работы пресса.
Для исключения влияния нестационарной части работы пресса, например периода разгона маховика, вычисление ресурсных параметров начинается в фиксированный момент модельного времени, который вводится как один из параметров модели SНАRN2. Его значение можно принимать равным времени начала первого цикла работы пресса. Расчетная динамическая грузоподъемность и срок службы подшипника вычисляются как расчетные переменные и выводятся с помощью универсальных индикаторов.
На рис. 24.19 показаны полученные моделированием графики расчета подшипников приводного вала пресса: расчетной динамической грузоподъемности С(R)1 и срока службы Т(R)1 левого подшипника, расчетной динамической
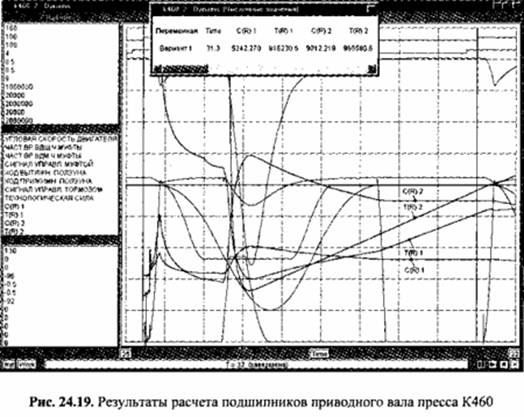
грузоподъемности С(R)2 и срока службы Т(R)2 правого подшипника. Значения в конце первого цикла работы пресса (t = 31,3 с) составили: С(R)1 - 5242,27 Н; С(R)2 - 9012,219 Н; Т(R)1 - 816230,5 ч; Т(R)2 - 965580,6 ч. Полученные значения намного превышают нормативные, что, видимо, является следствием выбора подшипников по конструктивным соображениям с учетом диаметра вала, определенного по условиям его прочности.
Для определения ресурсных параметров подшипников при нагружении пресса различными технологическими операциями следует выполнить моделирование работы пресса в составном цикле, содержащем циклы с графиками деформирующей силы на каждой операции. Во внимание следует принимать значения ресурсных параметров в конце составного цикла работы пресса.
При расчете ресурсных параметров подшипников качения путем математического моделирования учитываются статические и динамические составляющие рабочих нагрузок подшипников, определяемые свойствами воспроизводимых привлеченными моделями элементов, а также переменный характер нагружения подшипников в течение цикла.
Для случаев представления моделью SНАRN2 подшипника скольжения в ней на каждом шаге интегрирования вычисляются в качестве расчетных переменные величины pv и р. Их выводят в виде графиков с помощью универсальных индикаторов и используют для оценки несущей способности подшипника.
Расчет зубчатых передач. В тихоходных зубчатых передачах кривошипных прессов максимальные нагрузки воспринимаются одними и теми же зубьями колеса. Это обстоятельство учтено при расчете допускаемой силы на ползуне кривошипного пресса по прочности тихоходной зубчатой передачи. Для быстроходных передач и шестерен тихоходной передачи каждый зуб периодически нагружается на всех фазах рабочего нагружения в течение цикла. Их расчет следует проводить на основе прямой оценки контактных и изгибных напряжений.
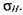 Они вычисляются как расчетные переменные Они вычисляются как расчетные переменные
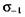 Контактные напряжения должны быть меньше соответствующих допускаемых, определенных с учетом коэффициента безопасности и коэффициента нагрузки. Контактные напряжения должны быть меньше соответствующих допускаемых, определенных с учетом коэффициента безопасности и коэффициента нагрузки.
|